tensorflow神经网络拟合非线性函数
Posted greathuman
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了tensorflow神经网络拟合非线性函数相关的知识,希望对你有一定的参考价值。
本实验通过建立一个含有两个隐含层的BP神经网络,拟合具有二次函数非线性关系的方程,并通过可视化展现学习到的拟合曲线,同时随机给定输入值,输出预测值,最后给出一些关键的提示。
源代码如下:
# -*- coding: utf-8 -*- import tensorflow as tf import numpy as np import matplotlib.pyplot as plt plotdata = { "batchsize":[], "loss":[] } def moving_average(a, w=11): if len(a) < w: return a[:] return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)] #生成模拟数据,二次函数关系 train_X = np.linspace(-1, 1, 100)[:, np.newaxis] train_Y = train_X*train_X + 5 * train_X + np.random.randn(*train_X.shape) * 0.3 #子图1显示模拟数据点 plt.figure(12) plt.subplot(221) plt.plot(train_X, train_Y, \'ro\', label=\'Original data\') plt.legend() # 创建模型 # 占位符 X = tf.placeholder("float",[None,1]) Y = tf.placeholder("float",[None,1]) # 模型参数 W1 = tf.Variable(tf.random_normal([1,10]), name="weight1") b1 = tf.Variable(tf.zeros([1,10]), name="bias1") W2 = tf.Variable(tf.random_normal([10,6]), name="weight2") b2 = tf.Variable(tf.zeros([1,6]), name="bias2") W3 = tf.Variable(tf.random_normal([6,1]), name="weight3") b3 = tf.Variable(tf.zeros([1]), name="bias3") # 前向结构 z1 = tf.matmul(X, W1) + b1 z2 = tf.nn.relu(z1) z3 = tf.matmul(z2, W2) + b2 z4 = tf.nn.relu(z3) z5 = tf.matmul(z4, W3) + b3 #反向优化 cost =tf.reduce_mean( tf.square(Y - z5)) learning_rate = 0.01 optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) #Gradient descent # 初始化变量 init = tf.global_variables_initializer() # 训练参数 training_epochs = 5000 display_step = 2 # 启动session with tf.Session() as sess: sess.run(init) for epoch in range(training_epochs+1): sess.run(optimizer, feed_dict={X: train_X, Y: train_Y}) #显示训练中的详细信息 if epoch % display_step == 0: loss = sess.run(cost, feed_dict={X: train_X, Y:train_Y}) print ("Epoch:", epoch, "cost=", loss) if not (loss == "NA" ): plotdata["batchsize"].append(epoch) plotdata["loss"].append(loss) print (" Finish") #图形显示 plt.subplot(222) plt.plot(train_X, train_Y, \'ro\', label=\'Original data\') plt.plot(train_X, sess.run(z5, feed_dict={X: train_X}), label=\'Fitted line\') plt.legend() plotdata["avgloss"] = moving_average(plotdata["loss"]) plt.subplot(212) plt.plot(plotdata["batchsize"], plotdata["avgloss"], \'b--\') plt.xlabel(\'Minibatch number\') plt.ylabel(\'Loss\') plt.title(\'Minibatch run vs Training loss\') plt.show() #预测结果 a=[[0.2],[0.3]] print ("x=[[0.2],[0.3]],z5=", sess.run(z5, feed_dict={X: a}))
运行结果如下:
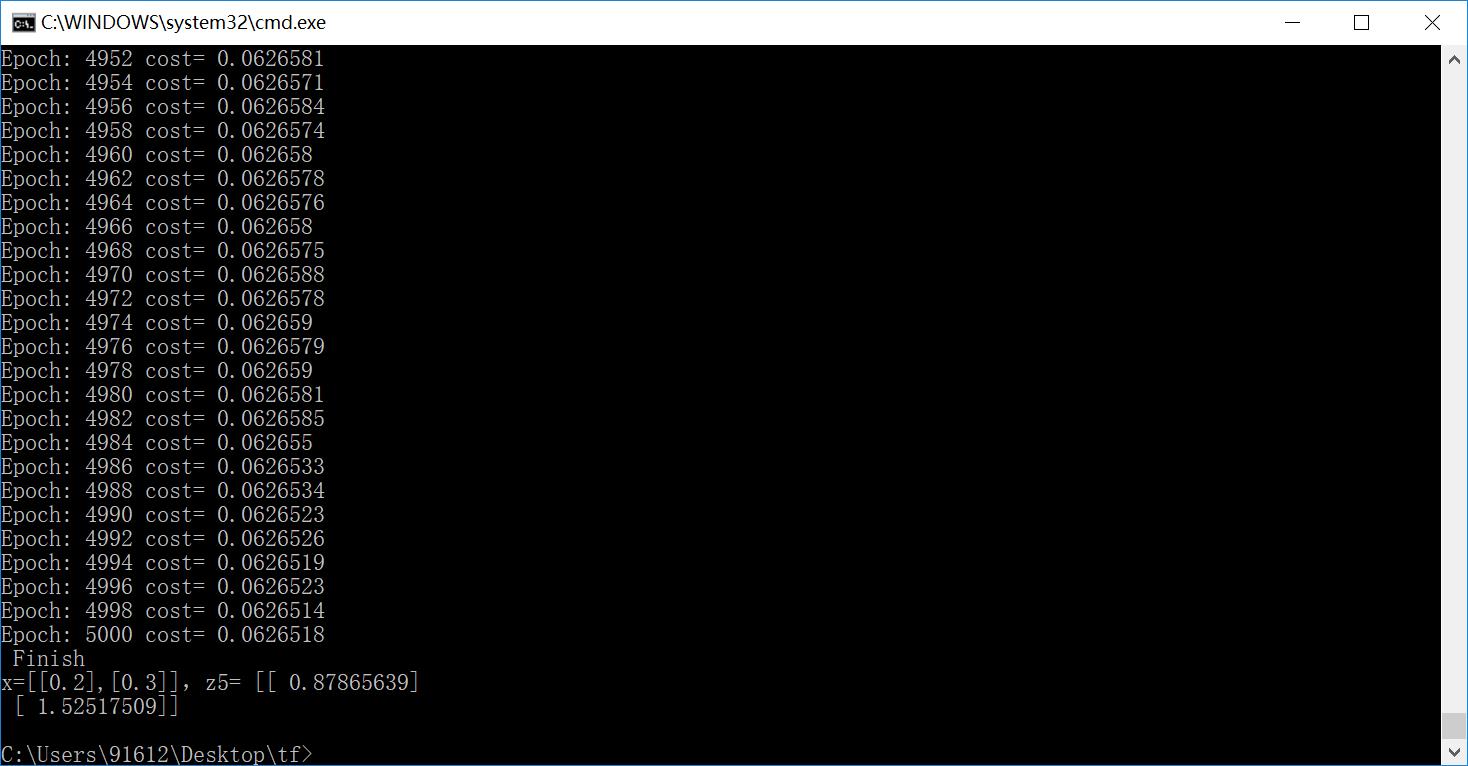
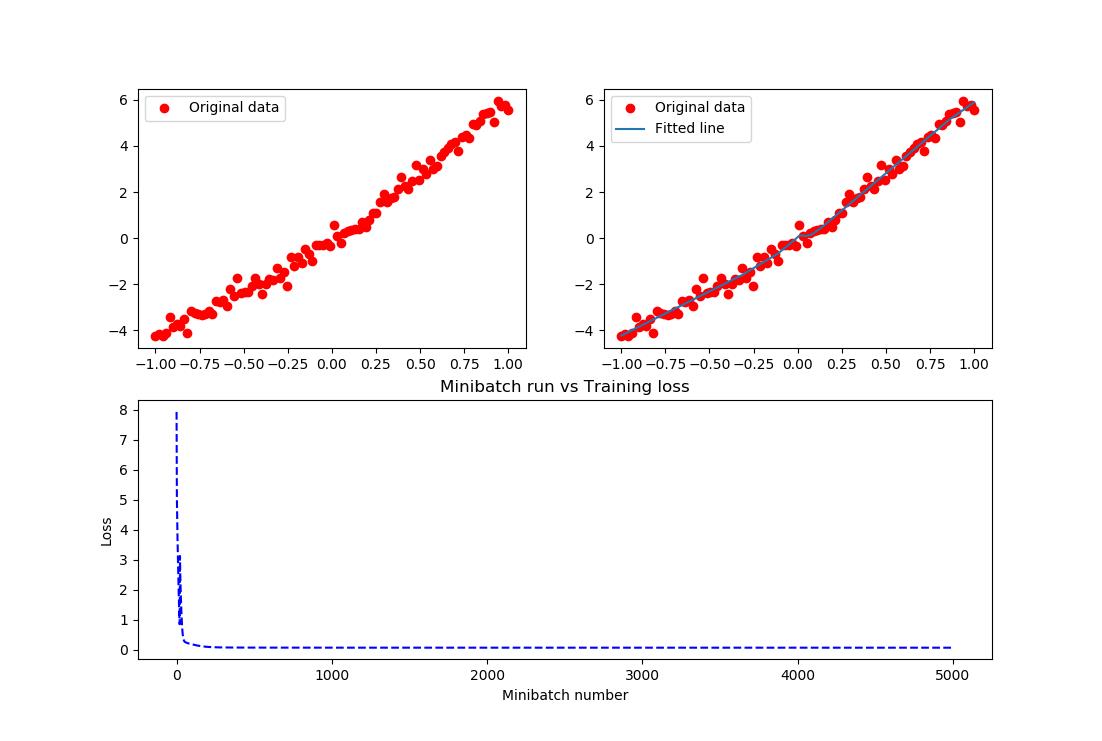
结果实在是太棒了,把这个关系拟合的非常好。在上述的例子中,需要进一步说明如下内容:
- 输入节点可以通过字典类型定义,而后通过字典的方法访问
input = { \'X\': tf.placeholder("float",[None,1]), \'Y\': tf.placeholder("float",[None,1]) }
sess.run(optimizer, feed_dict={input[\'X\']: train_X, input[\'Y\']: train_Y})
直接定义输入节点的方法是不推荐使用的。
- 变量也可以通过字典类型定义,例如上述代码可以改为:
parameter = { \'W1\': tf.Variable(tf.random_normal([1,10]), name="weight1"), \'b1\': tf.Variable(tf.zeros([1,10]), name="bias1"), \'W2\': tf.Variable(tf.random_normal([10,6]), name="weight2"), \'b2\': tf.Variable(tf.zeros([1,6]), name="bias2"), \'W3\': tf.Variable(tf.random_normal([6,1]), name="weight3"), \'b3\': tf.Variable(tf.zeros([1]), name="bias3") }
z1 = tf.matmul(X, parameter[\'W1\']) +parameter[\'b1\']
在上述代码中练习保存/载入模型,代码如下:
# -*- coding: utf-8 -*- import tensorflow as tf import numpy as np import matplotlib.pyplot as plt plotdata = { "batchsize":[], "loss":[] } def moving_average(a, w=11): if len(a) < w: return a[:] return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)] #生成模拟数据,二次函数关系 train_X = np.linspace(-1, 1, 100)[:, np.newaxis] train_Y = train_X*train_X + 5 * train_X + np.random.randn(*train_X.shape) * 0.3 #子图1显示模拟数据点 plt.figure(12) plt.subplot(221) plt.plot(train_X, train_Y, \'ro\', label=\'Original data\') plt.legend() # 创建模型 # 字典型占位符 input = {\'X\':tf.placeholder("float",[None,1]), \'Y\':tf.placeholder("float",[None,1])} # X = tf.placeholder("float",[None,1]) # Y = tf.placeholder("float",[None,1]) # 模型参数 parameter = {\'W1\':tf.Variable(tf.random_normal([1,10]), name="weight1"), \'b1\':tf.Variable(tf.zeros([1,10]), name="bias1"), \'W2\':tf.Variable(tf.random_normal([10,6]), name="weight2"),\'b2\':tf.Variable(tf.zeros([1,6]), name="bias2"), \'W3\':tf.Variable(tf.random_normal([6,1]), name="weight3"), \'b3\':tf.Variable(tf.zeros([1]), name="bias3")} # W1 = tf.Variable(tf.random_normal([1,10]), name="weight1") # b1 = tf.Variable(tf.zeros([1,10]), name="bias1") # W2 = tf.Variable(tf.random_normal([10,6]), name="weight2") # b2 = tf.Variable(tf.zeros([1,6]), name="bias2") # W3 = tf.Variable(tf.random_normal([6,1]), name="weight3") # b3 = tf.Variable(tf.zeros([1]), name="bias3") # 前向结构 z1 = tf.matmul(input[\'X\'], parameter[\'W1\']) + parameter[\'b1\'] z2 = tf.nn.relu(z1) z3 = tf.matmul(z2, parameter[\'W2\']) + parameter[\'b2\'] z4 = tf.nn.relu(z3) z5 = tf.matmul(z4, parameter[\'W3\']) + parameter[\'b3\'] #反向优化 cost =tf.reduce_mean( tf.square(input[\'Y\'] - z5)) learning_rate = 0.01 optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) #Gradient descent # 初始化变量 init = tf.global_variables_initializer() # 训练参数 training_epochs = 5000 display_step = 2 # 生成saver saver = tf.train.Saver() savedir = "model/" # 启动session with tf.Session() as sess: sess.run(init) for epoch in range(training_epochs+1): sess.run(optimizer, feed_dict={input[\'X\']: train_X, input[\'Y\']: train_Y}) #显示训练中的详细信息 if epoch % display_step == 0: loss = sess.run(cost, feed_dict={input[\'X\']: train_X, input[\'Y\']:train_Y}) print ("Epoch:", epoch, "cost=", loss) if not (loss == "NA" ): plotdata["batchsize"].append(epoch) plotdata["loss"].append(loss) print (" Finish") #保存模型 saver.save(sess, savedir+"mymodel.cpkt") #图形显示 plt.subplot(222) plt.plot(train_X, train_Y, \'ro\', label=\'Original data\') plt.plot(train_X, sess.run(z5, feed_dict={input[\'X\']: train_X}), label=\'Fitted line\') plt.legend() plotdata["avgloss"] = moving_average(plotdata["loss"]) plt.subplot(212) plt.plot(plotdata["batchsize"], plotdata["avgloss"], \'b--\') plt.xlabel(\'Minibatch number\') plt.ylabel(\'Loss\') plt.title(\'Minibatch run vs Training loss\') plt.show() #预测结果 #在另外一个session里面载入保存的模型,再测试 a=[[0.2],[0.3]] with tf.Session() as sess2: #sess2.run(tf.global_variables_initializer())可有可无,因为下面restore会载入参数,相当于本次调用的初始化 saver.restore(sess2, "model/mymodel.cpkt") print ("x=[[0.2],[0.3]],z5=", sess2.run(z5, feed_dict={input[\'X\']: a}))
生成如下目录:
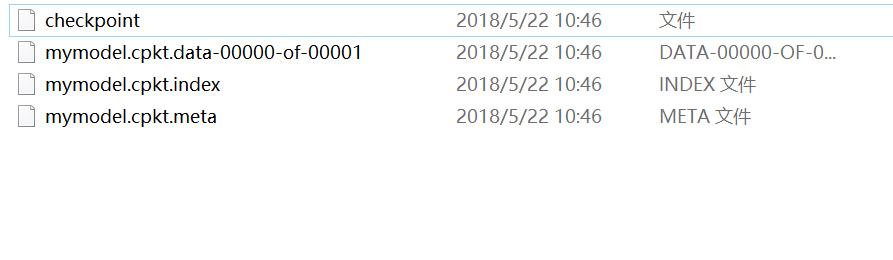
上述代码模型的载入没有利用到检查点文件,显得不够智能,还需用户去查找指定某一模型,那在很多算法项目中是不需要用户去找的,而可以通过检查点找到保存的模型。例如:
# -*- coding: utf-8 -*- import tensorflow as tf import numpy as np import matplotlib.pyplot as plt plotdata = { "batchsize":[], "loss":[] } def moving_average(a, w=11): if len(a) < w: return a[:] return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)] #生成模拟数据,二次函数关系 train_X = np.linspace(-1, 1, 100)[:, np.newaxis] train_Y = train_X*train_X + 5 * train_X + np.random.randn(*train_X.shape) * 0.3 #子图1显示模拟数据点 plt.figure(12) plt.subplot(221) plt.plot(train_X, train_Y, \'ro\', label=\'Original data\') plt.legend() # 创建模型 # 字典型占位符 input = {\'X\':tf.placeholder("float",[None,1]), \'Y\':tf.placeholder("float",[None,1])} # X = tf.placeholder("float",[None,1]) # Y = tf.placeholder("float",[None,1]) # 模型参数 parameter = {\'W1\':tf.Variable(tf.random_normal([1,10]), name="weight1"), \'b1\':tf.Variable(tf.zeros([1,10]), name="bias1"), \'W2\':tf.Variable(tf.random_normal([10,6]), name="weight2"),\'b2\':tf.Variable(tf.zeros([1,6]), name="bias2"), \'W3\':tf.Variable(tf.random_normal([6,1]), name="weight3"), \'b3\':tf.Variable(tf.zeros([1]), name="bias3")} # W1 = tf.Variable(tf.random_normal([1,10]), name="weight1") # b1 = tf.Variable(tf.zeros([1,10]), name="bias1") # W2 = tf.Variable(tf.random_normal([10,6]), name="weight2") # b2 = tf.Variable(tf.zeros([1,6]), name="bias2") # W3 = tf.Variable(tf.random_normal([6,1]), name="weight3") # b3 = tf.Variable(tf.zeros([1]), name="bias3") # 前向结构 z1 = tf.matmul(input[\'X\'], parameter[\'W1\']) + parameter[\'b1\'] z2 = tf.nn.relu(z1) z3 = tf.matmul(z2, parameter[\'W2\']) + parameter[\'b2\'] z4 = tf.nn.relu(z3) z5 = tf.matmul(z4, parameter[\'W3\']) + parameter[\'b3\'] #反向优化 cost =tf.reduce_mean( tf.square(input[\'Y\'] - z5)) learning_rate = 0.01 optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) #Gradient descent # 初始化变量 init = tf.global_variables_initializer() # 训练参数 training_epochs = 5000 display_step = 2 # 生成saver saver = tf.train.Saver(max_to_keep=1) savedir = "model/" # 启动session with tf.Session() as sess: sess.run(init) for epoch in range(training_epochs+1): sess.run(optimizer, feed_dict={input[\'X\']: train_X, input[\'Y\']: train_Y}) saver.save(sess, savedir+"mymodel.cpkt",global_step=epoch) #显示训练中的详细信息 if epoch % display_step == 0: loss = sess.run(cost, feed_dict={input[\'X\']: train_X, input[\'Y\']:train_Y}) print ("Epoch:", epoch, "cost=", loss) if not (loss == "NA" ): plotdata["batchsize"].append(epoch) plotdata["loss"].append(loss) print (" Finish") #图形显示 plt.subplot(222) plt.plot(train_X, train_Y, \'ro\', label=\'Original data\') plt.plot(train_X, sess.run(z5, feed_dict={input[\'X\']: train_X}), label=\'Fitted line\') plt.legend() plotdata["avgloss"] = moving_average(plotdata["loss"]) plt.subplot(212) plt.plot(plotdata["batchsize"], plotdata["avgloss"], \'b--\') plt.xlabel(\'Minibatch number\') plt.ylabel(\'Loss\') plt.title(\'Minibatch run vs Training loss\') plt.show() #预测结果 #在另外一个session里面载入保存的模型,再测试 a=[[0.2],[0.3]] load=5000 with tf.Session() as sess2: #sess2.run(tf.global_variables_initializer())可有可无,因为下面restore会载入参数,相当于本次调用的初始化 #saver.restore(sess2, "model/mymodel.cpkt") saver.restore(sess2, "model/mymodel.cpkt-" + str(load)) print ("x=[[0.2],[0.3]],z5=", sess2.run(z5, feed_dict={input[\'X\']: a})) #通过检查点文件载入保存的模型 with tf.Session() as sess3: ckpt = tf.train.get_checkpoint_state(savedir) if ckpt and ckpt.model_checkpoint_path: saver.restore(sess3, ckpt.model_checkpoint_path) print ("x=[[0.2],[0.3]],z5=", sess3.run(z5, feed_dict={input[\'X\']: a})) #通过检查点文件载入最新保存的模型 with tf.Session() as sess4: ckpt = tf.train.latest_checkpoint(savedir) if ckpt!=None: saver.restore(sess4, ckpt) print ("x=[[0.2],[0.3]],z5=", sess4.run(z5, feed_dict={input[\'X\']: a}))
而通常情况下,上述两种通过检查点载入模型参数的结果是一样的,主要是因为不管用户保存了多少个模型文件,都会被记录在唯一一个检查点文件中,这个指定保存模型个数的参数就是max_to_keep,例如:
saver = tf.train.Saver(max_to_keep=3)
而检查点都会默认用最新的模型载入,忽略了之前的模型,因此上述两个检查点载入了同一个模型,自然最后输出的测试结果是一致的。保存的三个模型如图:
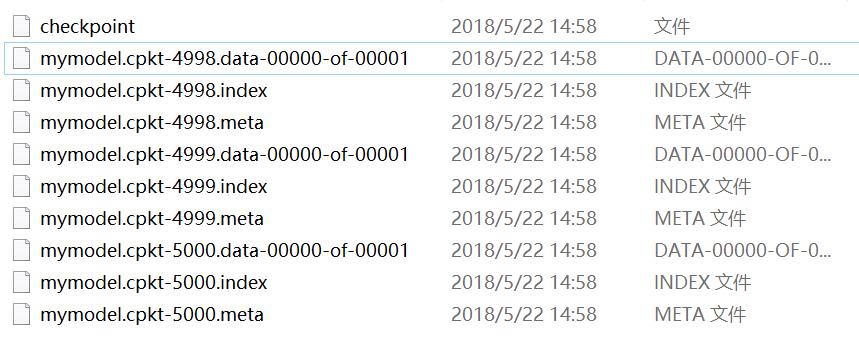
接下来,为什么上面的变量,需要给它对应的操作起个名字,而且是不一样的名字呢?像weight1、bias1等等。大家都知道,名字这个东西太重要了,通过它可以访问我们想访问的变量,也就可以对其进行一些操作。例如:
- 显示模型的内容
不同版本的函数会有些区别,本文试验的版本是1.7.0,代码例如:
# -*- coding: utf-8 -*- import tensorflow as tf from tensorflow.python.tools import inspect_checkpoint as chkp #显示全部变量的名字和值 chkp.print_tensors_in_checkpoint_file("model/mymodel.cpkt-5000", all_tensor_names=\'\', tensor_name=\'\', all_tensors=True) #显示指定名字变量的值 chkp.print_tensors_in_checkpoint_file("model/mymodel.cpkt-5000", all_tensor_names=\'\', tensor_name=\'weight1\', all_tensors=False) chkp.print_tensors_in_checkpoint_file("model/mymodel.cpkt-5000", all_tensor_names=\'\', tensor_name=\'bias1\', all_tensors=False)
运行结果如下图:
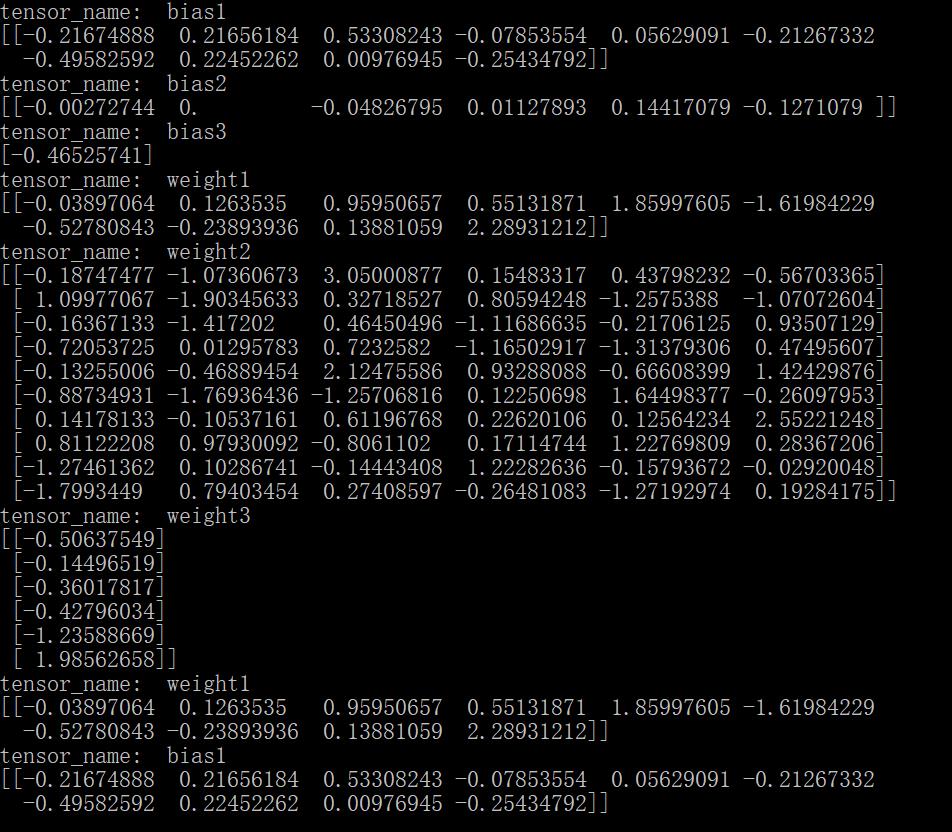
相反如果对不同变量的操作用了同一个name,系统将会自动对同名称操作排序,例如:
# -*- coding: utf-8 -*- import tensorflow as tf from tensorflow.python.tools import inspect_checkpoint as chkp #显示全部变量的名字和值 chkp.print_tensors_in_checkpoint_file("model/mymodel.cpkt-50", all_tensor_names=\'\', tensor_name=\'\', all_tensors=True) #显示指定名字变量的值 chkp.print_tensors_in_checkpoint_file("model/mymodel.cpkt-50", all_tensor_names=\'\', tensor_name=\'weight\', all_tensors=False) chkp.print_tensors_in_checkpoint_file("model/mymodel.cpkt-50", all_tensor_names=\'\', tensor_name=\'bias\', all_tensors=False)
结果为:
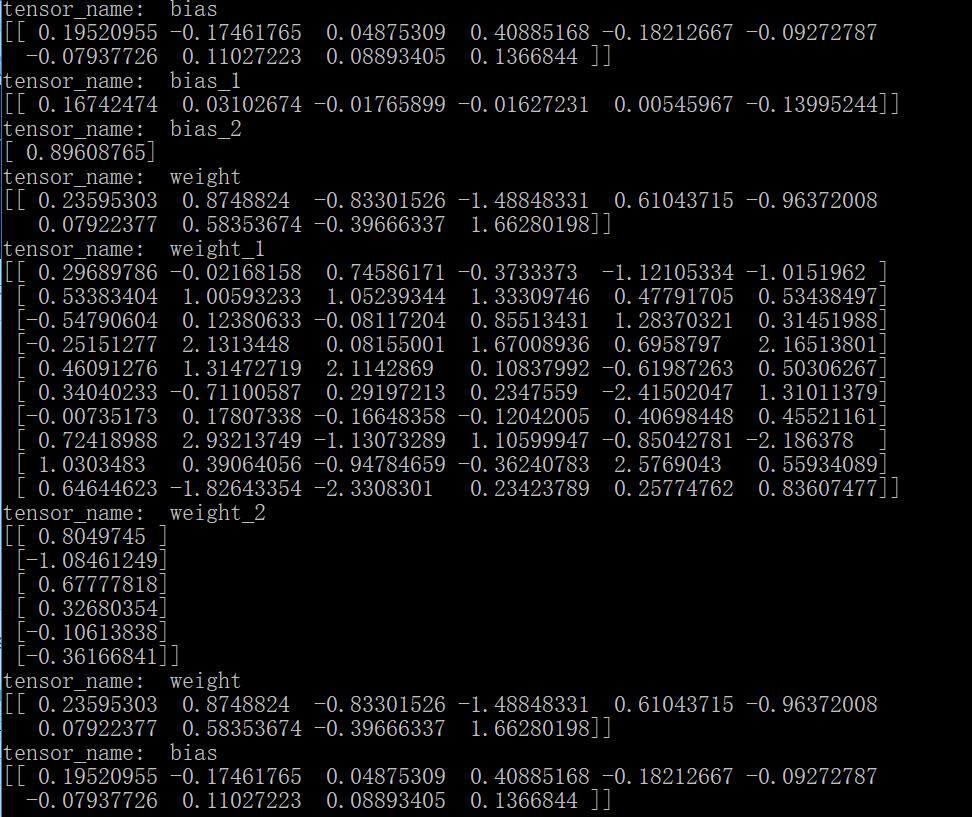
需要注意的是因为对所有同名的变量排序之后,真正的变量名已经变了,所以,当指定查看某一个变量的值时,其实输出的是第一个变量的值,因为它的名称还保留着不变。另外,也可以通过变量的name属性查看其操作名。
- 按名字保存变量
可以通过指定名称来保存变量;注意如果名字如果搞混了,名称所对应的值也就搞混了,比如:
#只保存这两个变量,并且这两个被搞混了 saver = tf.train.Saver({\'weight\': parameter[\'b2\'], \'bias\':parameter[\'W1\']}) # -*- coding: utf-8 -*- import tensorflow as tf from tensorflow.python.tools import inspect_checkpoint as chkp #显示全部变量的名字和值 chkp.print_tensors_in_checkpoint_file("model/mymodel.cpkt-50", all_tensor_names=\'\', tensor_name=\'\', all_tensors=True) #显示指定名字变量的值 chkp.print_tensors_in_checkpoint_file("model/mymodel.cpkt-50", all_tensor_names=\'\', tensor_name=\'weight\', all_tensors=False) chkp.print_tensors_in_checkpoint_file("model/mymodel.cpkt-50", all_tensor_names=\'\', tensor_name=\'bias\', all_tensors=False)
此时的结果是:
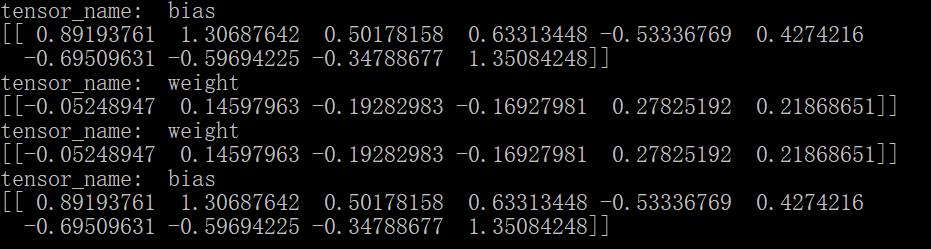
这样,模型按照我们的想法保存了参数,注意不能搞混变量和其对应的名字。
以上是关于tensorflow神经网络拟合非线性函数的主要内容,如果未能解决你的问题,请参考以下文章