数据结构——二叉树 前序中序后序层次遍历及非递归实现 查找统计个数比较求深度的递归实现(转)

Posted 2020-11-07 Compute

一、基本概念

每个结点最多有两棵子树，左子树和右子树，次序不可以颠倒。

性质：

1、非空二叉树的第n层上至多有2^(n-1)个元素。

2、深度为h的二叉树至多有2^h-1个结点。

满二叉树：所有终端都在同一层次，且非终端结点的度数为2。

在满二叉树中若其深度为h，则其所包含的结点数必为2^h-1。

完全二叉树：除了最大的层次即成为一颗满二叉树且层次最大那层所有的结点均向左靠齐，即集中在左面的位置上，不能有空位置。

对于完全二叉树，设一个结点为i则其父节点为i/2，2i为左子节点，2i+1为右子节点。

二、存储结构

顺序存储：

将数据结构存在一块固定的数组中。

[cpp] view plain copy

 

1. #define LENGTH 100  
2. typedef char datatype;  
3. typedef struct node{  
4.     datatype data;  
5.     int lchild,rchild;  
6.     int parent;  
7. }Node;  
8.   
9. Node tree[LENGTH];  
10. int length;  
11. int root;  

   虽然在遍历速度上有一定的优势，但因所占空间比较大，是非主流二叉树。二叉树通常以链式存储。

链式存储：

[cpp] view plain copy

 

1. typedef char datatype;  
2.   
3. typedef struct BinNode{  
4.     datatype data;  
5.     struct BinNode* lchild;  
6.     struct BinNode* rchild;  
7. }BinNode;  
8.   
9. typedef BinNode* bintree;          //bintree本身是个指向结点的指针  

 三、二叉树的遍历

遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历，中序遍历，后序遍历。

前序遍历：根节点->左子树->右子树

中序遍历：左子树->根节点->右子树

后序遍历：左子树->右子树->根节点

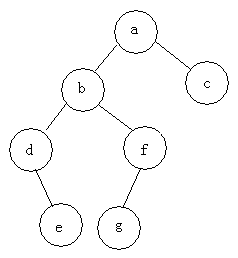
例如：求下面树的三种遍历

 

前序遍历：abdefgc

中序遍历：debgfac

后序遍历：edgfbca

四、遍历的实现

递归实现(以前序遍历为例，其他的只是输出的位置稍有不同)

[cpp] view plain copy

 

1. void preorder(bintree t){  
2.     if(t){  
3.         printf("%c ",t->data);  
4.         preorder(t->lchild);  
5.         preorder(t->rchild);  
6.     }  
7. }  

非递归的实现

因为当遍历过根节点之后还要回来，所以必须将其存起来。考虑到后进先出的特点，选用栈存储。数量确定，以顺序栈存储。

[cpp] view plain copy

 

1. #define SIZE 100  
2. typedef struct seqstack{  
3.     bintree data[SIZE];  
4.     int tag[SIZE];   //为后续遍历准备的  
5.     int top;     //top为数组的下标  
6. }seqstack;  
7.   
8. void push(seqstack *s,bintree t){  
9.   
10.     if(s->top == SIZE){  
11.         printf("the stack is full\n");  
12.     }else{  
13.         s->top++;  
14.         s->data[s->top]=t;  
15.     }  
16. }  
17.   
18. bintree pop(seqstack *s){  
19.     if(s->top == -1){  
20.         return NULL;  
21.     }else{  
22.         s->top--;  
23.         return s->data[s->top+1];  
24.     }  
25. }  

1、前序遍历 

[cpp] view plain copy

 

1. void preorder_dev(bintree t){  
2.     seqstack s;  
3.     s.top = -1;     //因为top在这里表示了数组中的位置，所以空为-1  
4.     if(!t){  
5.         printf("the tree is empty\n");  
6.     }else{  
7.         while(t || s.stop != -1){  
8.             while(t){    //只要结点不为空就应该入栈保存，与其左右结点无关      
9.                   printf("%c ",t->data);  
10.                 push(&s,t);  
11.                 t= t->lchild;  
12.             }  
13.             t=pop(&s);  
14.             t=t->rchild;  
15.         }  
16.     }  
17. }  

 

 2、中序遍历

 

[cpp] view plain copy

 

1. void midorder(bintree t){  
2.     seqstack s;  
3.     s.top = -1;  
4.     if(!t){  
5.         printf("the tree is empty!\n");  
6.     }else{  
7.         while(t ||s.top != -1){  
8.             while(t){  
9.                 push(&s,t);  
10.                 t= t->lchild;  
11.             }  
12.             t=pop(&s);  
13.             printf("%c ",t->data);  
14.             t=t->rchild;  
15.         }  
16.     }  
17. }  

 

3、后序遍历

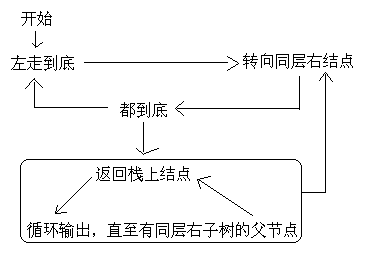
因为后序遍历最后还要要访问根结点一次，所以要访问根结点两次。采取夹标志位的方法解决这个问题。

这段代码非常纠结，对自己有信心的朋友可以尝试独立写一下。反正我是写了很长时间。逻辑不难，我画了一张逻辑图：

 代码：

 

[cpp] view plain copy

 

1. void postorder_dev(bintree t){  
2.     seqstack s;  
3.     s.top = -1;  
4.     if(!t){  
5.         printf("the tree is empty!\n");  
6.     }else{  
7.         while(t || s.top != -1){    //栈空了的同时t也为空。  
8.             while(t){  
9.                 push(&s,t);  
10.                 s.tag[s.top] = 0;   //设置访问标记，0为第一次访问，1为第二次访问  
11.                 t= t->lchild;  
12.             }  
13.             if(s.tag[s.top] == 0){  //第一次访问时，转向同层右结点  
14.                 t= s.data[s.top];   //左走到底时t是为空的，必须有这步！  
15.                 s.tag[s.top]=1;       
16.                 t=t->rchild;  
17.             }else {  
18.                 while (s.tag[s.top] == 1){ //找到栈中下一个第一次访问的结点，退出循环时并没有pop所以为其左子结点  
19.                     t = pop(&s);  
20.                     printf("%c ",t->data);  
21.                 }  
22.                 t = NULL; //必须将t置空。跳过向左走，直接向右走  
23.             }  
24.         }  
25.     }  
26. }  

 4、层次遍历：即每一层从左向右输出

元素需要储存有先进先出的特性，所以选用队列存储。

队列的定义：

[cpp] view plain copy

 

1. #define MAX 1000  
2.   
3. typedef struct seqqueue{  
4.     bintree data[MAX];  
5.     int front;  
6.     int rear;  
7. }seqqueue;  
8.   
9.   
10. void enter(seqqueue *q,bintree t){  
11.     if(q->rear == MAX){  
12.         printf("the queue is full!\n");  
13.     }else{  
14.         q->data[q->rear] = t;  
15.         q->rear++;  
16.     }  
17. }  
18.   
19. bintree del(seqqueue *q){  
20.     if(q->front == q->rear){  
21.         return NULL;  
22.     }else{  
23.         q->front++;  
24.         return q->data[q->front-1];  
25.     }  
26. }  

遍历实现 

[cpp] view plain copy

 

1. void level_tree(bintree t){  
2.     seqqueue q;  
3.     bintree temp;  
4.     q.front = q.rear = 0;  
5.     if(!t){  
6.         printf("the tree is empty\n");  
7.         return ;  
8.     }  
9.     enter(&q,t);  
10.     while(q.front != q.rear){  
11.         t=del(&q);  
12.         printf("%c ",t->data);  
13.         if(t->lchild){  
14.             enter(&q,t->lchild);  
15.         }  
16.         if(t->rchild){  
17.             enter(&q,t->rchild);  
18.         }  
19.     }  
20. }  

 

5、利用前序遍历的结果生成二叉树

[cpp] view plain copy

 

1. //递归调用，不存点，想的时候只关注于一个点，因为还会回来的，不要跟踪程序运行，否则容易多加循环  
2.   
3. void createtree(bintree *t){        
4.     datatype c;  
5.     if((c=getchar()) == ‘#‘)  
6.         *t = NULL;  
7.     else{  
8.         *t = (bintree)malloc(sizeof(BinNode));  
9.         (*t)->data = c;  
10.         createtree(&(*t)->lchild);  
11.         createtree(&(*t)->rchild);  
12.     }  
13. }  

6、二叉树的查找

[cpp] view plain copy

 

1. bintree search_tree(bintree t,datatype x){  
2.     if(!t){  
3.         return NULL;  
4.     }  
5.     if(t->data == x){  
6.         return t;  
7.     }else{  
8.         if(!search_tree(t->lchild,x)){  
9.             return search_tree(t->rchild,x);  
10.         }  
11.         return t;  
12.     }  
13. }  

7、统计结点个数

[cpp] view plain copy

 

1. int count_tree(bintree t){  
2.     if(t){  
3.         return (count_tree(t->lchild)+count_tree(t->rchild)+1);  
4.     }  
5.     return 0;  
6. }  

8、比较两个树是否相同

[cpp] view plain copy

 

1. int is_equal(bintree t1,bintree t2){  
2.     if(!t1 && !t2){      //都为空就相等  
3.         return 1;  
4.     }  
5.     if(t1 && t2 && t1->data == t2->data){      //有一个为空或数据不同就不判断了  
6.         if(is_equal(t1->lchild,t2->lchild))  
7.             if(is_equal(t1->rchild,t2->rchild)){  
8.                 return 1;  
9.             }  
10.     }  
11.     return 0;  
12. }  

9、求二叉树的深度

[cpp] view plain copy

 

1. int hight_tree(bintree t){  
2. int h,left,right;  
3. if(!t){  
4. return 0;  
5.     }  
6.     left = hight_tree(t->lchild);  
7.     right = hight_tree(t->rchild);  
8.     h = (left>right?left:right)+1;  
9. return h;  
10. }  

 

1 二叉树的深度

题目： 
输入一个二叉树的根节点，求该树的深度。从根节点到叶子节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度包含的节点数为为树的深度，即二叉树节点的层数。

二叉树的节点定义： 
假定二叉树的节点定义如下：

struct BinaryTreeNode{
    int m_value;
    BinaryTreeNode* m_pLeft;
    BinaryTreeNode* m_pRight;
};

二叉树示例： 
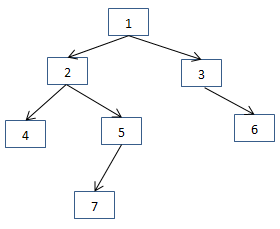
以图深度为四的二叉树为例，其先先根遍历序列为：{1,2,4,5,7,3,6}，中根遍历序列为：{4,2,7,5,1,3,6}，根据先根序列和中根序列即可构造唯一的二叉树，构造的具体实现可参见：二叉树的构造与遍历。很显然，该二叉树有4层节点，所以其高度是４。

求解思路： 
根据题目的定义，我们可以用先根次序来遍历二叉树中所有根节点到叶节点的路径，来得到最长的路径就是二叉树的高度。但是这样的代码量较为冗长，我们可以采用递归的方式解决。

我们可以从根节点即左右子树来理解二叉树的深度。对于任意一棵非空二叉树，有如下四种情况：

（1）如果一颗树只有一个节点，它的深度是1；

（2）如果根节点只有左子树而没有右子树，那么二叉树的深度应该是其左子树的深度加1；

（3）如果根节点只有右子树而没有左子树，那么二叉树的深度应该是其右树的深度加1；

（4）如果根节点既有左子树又有右子树，那么二叉树的深度应该是其左右子树的深度较大值加1；

实现代码：

int treeDepth(BinaryTreeNode* root){
    if(root==NULL){
        return 0;
    }
    int nLeft=treeDepth(root->m_pLeft);
    int nRight=treeDepth(root->m_pRight);
    return nLeft>nRight?nLeft+1:nRight+1;
}

2 二叉树的宽度

题目： 
给定一颗二叉树，求二叉树的宽度。

宽度的定义： 
二叉树的宽度定义为具有最多结点数的层中包含的结点数。

比如上图中，第1层有1个节点， 第2层有2个节点， 第3层有4个节点， 第4层有1个节点，可知，第3层的结点数最多，所以这棵二叉树的宽度就是4。

求解思路： 
这里需要用到二叉树的层次遍历，即广度优先周游。在层次遍历的过程中，通过读取队列中保留的上一层的节点数来记录每层的节点数，以获取所有层中最大的节点数。关于二叉树的广度优先周游，参考：二叉树的构造与遍历。

具体实现：

//求二叉树的宽度  
int treeWidth(BinaryTreeNode *pRoot){  
    if (pRoot == NULL)
        return 0;  

    int nLastLevelWidth = 0;//记录上一层的宽度  
    int nCurLevelWidth = 0;//记录当前层的宽度  

    queue<BinaryTreeNode*> myQueue;  
    myQueue.push(pRoot);//将根节点入队列  
    int nWidth = 1;//二叉树的宽度  
    nLastLevelWidth = 1;      
    BinaryTreeNode *pCur = NULL;  

    while (!myQueue.empty())//队列不空  
    {  
        while (nLastLevelWidth!= 0){  
            pCur = myQueue.front();//取出队列头元素  
            myQueue.pop();//将队列头元素出对  

            if (pCur->m_pLeft != NULL)  
                myQueue.push(pCur->m_pLeft);   

            if (pCur->m_pRight != NULL)  
                myQueue.push(pCur->m_pRight); 
            nLastLevelWidth--;  
        }  

        nCurLevelWidth = myQueue.size();  
        nWidth = nCurLevelWidth > nWidth ? nCurLevelWidth : nWidth;  
        nLastLevelWidth = nCurLevelWidth;  
    }  
    return nWidth;  
}  

---

参考文献

[1]剑指Offer.何海涛.电子工业出版社. 
[2]求二叉树的深度和宽度