线段树普及版
Posted $mathcal{color{skyblue}{\_Orch
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线段树普及版相关的知识,希望对你有一定的参考价值。
一、简介线段树
\(ps\): 此处以询问区间和为例
线段树之所以称为“树”,是因为其具有树的结构特性。线段树由于本身是专门用来处理区间问题的(包括\(RMQ\)、\(RSQ\)问题等),所以其结构可以近似的看做一棵二叉查找树:
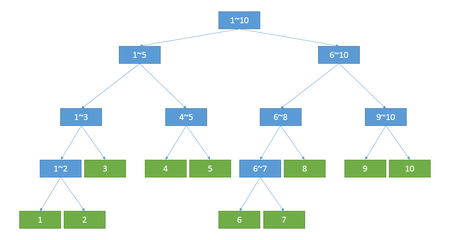
\(emmmmm\)图是从网上偷的
对于每一个子节点而言,都表示整个序列中的一段子区间;对于每个叶子节点而言,都表示序列中的单个元素信息;子节点不断向自己的父亲节点传递信息,而父节点存储的信息则是他的每一个子节点信息的整合。
有没有觉得很熟悉?对,线段树就是分块思想的树化,或者说是对于信息处理的二进制化——用于达到\(O(logn)\)级别的处理速度,\(log\)以\(2\)为底。(其实以几为底都只不过是个常数,可忽略)。而分块的思想,则是可以用一句话总结为:通过将整个序列分为有穷个小块,对于要查询的一段区间,总是可以整合成\(k\)个所分块与\(m\)个单个元素的信息的并\((0<=k,m<=\sqrt{n})\)。但普通的分块不能高效率地解决很多问题,所以作为\(log\)级别的数据结构,线段树应运而生。
二、逐步分析线段树的构造实现
1、建树与维护
由于二叉树的自身特性,对于每个父亲节点的编号\(i\),他的两个儿子的编号分别是\(2i\)和\(2i+1\),所以我们考虑写两个\(O(1)\)的取儿子函数:
int n;
int ans[MAXN*4];
inline int ls(int p){
return p<<1;
}//左儿子
inline int rs(int p){
return p<<1|1;
}//右儿子 \(ps:\)此处的\(inline\)可以有效防止无需入栈的信息入栈,节省时间和空间
那么根据线段树的服务对象,可以得到线段树的维护:
void push_up_sum(int p){
t[p]=t[lc(p)]+t[rc(p)];
}// 向上不断维护区间操作
void push_up_min(int p)//max
{
t[p]=min(t[lc(p)],t[rc(p));
//t[p]=max(t[lc(p)],t[rc(p));
}此处一定要注意,\(push up\)操作的目的是为了维护父子节点之间的逻辑关系。当我们递归建树时,对于每一个节点我们都需要遍历一遍,并且电脑中的递归实际意义是先向底层递归,然后从底层向上回溯,所以开始递归之后必然是先去整合子节点的信息,再向它们的祖先回溯整合之后的信息。(这其实是正确性的证明啦)
那么对于建树,由于二叉树自身的父子节点之间的可传递关系,所以可以考虑递归建树(\(emmmm\)之前好像不小心剧透了\(qwq\)),并且在建树的同时,我们应该维护父子节点的关系:
void build(ll p,ll l,ll r)
{
if(l==r){ans[p]=a[l];return ;}
//如果左右区间相同,那么必然是叶子节点啦,只有叶子节点是被真实赋值的
ll mid=(l+r)>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
//此处由于我们采用的是二叉树,所以对于整个结构来说,可以用二分来降低复杂度,否则树形结构则没有什么明显的优化
push_up(p);
//此处由于我们是要通过子节点来维护父亲节点,所以pushup的位置应当是在回溯时。
} 2、接下来谈区间修改
为什么不讨论单点修改呢\(qwq\)?因为其实很显然,单点修改就是区间修改的一个子问题而已,即区间长度为\(1\)时进行的区间修改操作罢了\(qwq\)
那么对于区间操作,我们考虑引入一个名叫“\(lazy\) \(tag\)”(懒标记)的东西——之所以称其“\(lazy\)”,是因为原本区间修改需要通过先改变叶子节点的值,然后不断地向上递归修改祖先节点直至到达根节点,时间复杂度最高可以到达\(O(nlogn)\)的级别。但当我们引入了懒标记之后,区间更新的期望复杂度就降到了\(O(logn)\)的级别且甚至会更低.
不扯淡了,聊正事:
(1)首先先来从分块思想上解释如何区间修改:
分块的思想是通过将整个序列分为有穷个小块,对于要查询的一段区间,总是可以整合成\(k\)个所分块与\(m\)个单个元素的信息的并\((0<=k,m<=logn)\)(小小修改了一下的上面的前言\(qwq\))
那么我们可以反过来思考这个问题:对于一个要修改的、长度为\(l\)的区间来说,总是可以看做由一个长度为\(2\)^\(log\)(\(\lfloor{n}\rfloor{}\))和剩下的元素(或者小区间组成)。那么我们就可以先将其拆分成线段树上节点所示的区间,之后分开处理:
如果单个元素被包含就只改变自己,如果整个区间被包含就修改整个区间
其实好像这个在分块里不是特别简单地实现,但是在线段树里,无论是元素还是区间都是线段树上的一个节点,所以我们不需要区分区间还是元素,加个判断就好。
(2)懒标记的正确打开方式
首先,懒标记的作用是记录每次、每个节点要更新的值,也就是\(delta\),但线段树的优点不在于全记录(全记录依然很慢qwq),而在于传递式记录:
** 整个区间都被操作,记录在公共祖先节点上;只修改了一部分,那么就记录在这部分的公共祖先上;如果四环以内只修改了自己的话,那就只改变自己。**
\(\rm{After}\) \(\rm{tha}t\),如果我们采用上述的优化方式的话,我们就需要在每次区间的查询修改时\(pushdown\)一次,以免重复或者冲突或者爆炸\(qwq\)
那么对于\(pushdown\)而言,其实就是纯粹的\(pushup\)的逆向思维(但不是逆向操作):
因为修改信息存在父节点上,所以要由父节点向下传导\(lazy\) \(tag\)
那么问题来了:怎么传导\(pushdown\)呢?这里很有意思,开始回溯时执行\(pushup\),因为是向上传导信息;那我们如果要让它向下更新,就调整顺序,在向下递归的时候\(pushdown\)不就好惹~\(qwq\):
inline void f(ll p,ll l,ll r,ll k)
{
tag[p]=tag[p]+k;
ans[p]=ans[p]+k*(r-l+1);
//由于是这个区间统一改变,所以ans数组要加元素个数次啦
}
//我们可以认识到,f函数的唯一目的,就是记录当前节点所代表的区间
inline void push_down(ll p,ll l,ll r)
{
ll mid=(l+r)>>1;
f(ls(p),l,mid,tag[p]);
f(rs(p),mid+1,r,tag[p]);
tag[p]=0;
//每次更新两个儿子节点。以此不断向下传递
}
inline void update(ll nl,ll nr,ll l,ll r,ll p,ll k)
{
//nl,nr为要修改的区间
//l,r,p为当前节点所存储的区间以及节点的编号
if(nl<=l&&r<=nr)
{
ans[p]+=k*(r-l+1);
tag[p]+=k;
return ;
}
push_down(p,l,r);
//回溯之前(也可以说是下一次递归之前,因为没有递归就没有回溯)
//由于是在回溯之前不断向下传递,所以自然每个节点都可以更新到
ll mid=(l+r)>>1;
if(nl<=mid)update(nl,nr,l,mid,ls(p),k);
if(nr>mid) update(nl,nr,mid+1,r,rs(p),k);
push_up(p);
//回溯之后
}(3)那么对于区间查询
没什么好说的,由于是信息的整合,所以还是要用到分块思想,我实在是不想再码一遍了\(qwq\)
ll query(ll q_x,ll q_y,ll l,ll r,ll p)
{
ll res=0;
if(q_x<=l&&r<=q_y)return ans[p];
ll mid=(l+r)>>1;
push_down(p,l,r);
if(q_x<=mid)res+=query(q_x,q_y,l,mid,ls(p));
if(q_y>mid) res+=query(q_x,q_y,mid+1,r,rs(p));
return res;
}最后贴高清无码的标程:
(还有,输入大数据一定不要用不加优化的cin/cout啊)
#include<iostream>
#include<cstdio>
#define MAXN 1000001
#define ll long long
using namespace std;
unsigned ll n,m,a[MAXN],ans[MAXN<<2],tag[MAXN<<2];
inline ll ls(ll x)
{
return x<<1;
}
inline ll rs(ll x)
{
return x<<1|1;
}
void scan()
{
cin>>n>>m;
for(ll i=1;i<=n;i++)
scanf("%lld",&a[i]);
}
inline void push_up(ll p)
{
ans[p]=ans[ls(p)]+ans[rs(p)];
}
void build(ll p,ll l,ll r)
{
tag[p]=0;
if(l==r){ans[p]=a[l];return ;}
ll mid=(l+r)>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
push_up(p);
}
inline void f(ll p,ll l,ll r,ll k)
{
tag[p]=tag[p]+k;
ans[p]=ans[p]+k*(r-l+1);
}
inline void push_down(ll p,ll l,ll r)
{
ll mid=(l+r)>>1;
f(ls(p),l,mid,tag[p]);
f(rs(p),mid+1,r,tag[p]);
tag[p]=0;
}
inline void update(ll nl,ll nr,ll l,ll r,ll p,ll k)
{
if(nl<=l&&r<=nr)
{
ans[p]+=k*(r-l+1);
tag[p]+=k;
return ;
}
push_down(p,l,r);
ll mid=(l+r)>>1;
if(nl<=mid)update(nl,nr,l,mid,ls(p),k);
if(nr>mid) update(nl,nr,mid+1,r,rs(p),k);
push_up(p);
}
ll query(ll q_x,ll q_y,ll l,ll r,ll p)
{
ll res=0;
if(q_x<=l&&r<=q_y)return ans[p];
ll mid=(l+r)>>1;
push_down(p,l,r);
if(q_x<=mid)res+=query(q_x,q_y,l,mid,ls(p));
if(q_y>mid) res+=query(q_x,q_y,mid+1,r,rs(p));
return res;
}
int main()
{
ll a1,b,c,d,e,f;
scan();
build(1,1,n);
while(m--)
{
scanf("%lld",&a1);
switch(a1)
{
case 1:{
scanf("%lld%lld%lld",&b,&c,&d);
update(b,c,1,n,1,d);
break;
}
case 2:{
scanf("%lld%lld",&e,&f);
printf("%lld\n",query(e,f,1,n,1));
break;
}
}
}
return 0;
}以上是关于线段树普及版的主要内容,如果未能解决你的问题,请参考以下文章