Given any signal \\(x\\in R^n\\), we can obtain sparse representation \\(\\theta\\in R^n\\) of \\(x\\) in two ways:
- Basis expansion: given sparse-inducing othonormal basis matrix \\(B\\in R^{n\\times n}\\), e.g., discrete cosine transform (DCT) matrix, iscrete wavelet transform (DWT) matrix, free-types filter banks of DWT etc. Precisely, we are finding sparse solution that satisfy:\\[y=B\\theta. \\]
2.Dictionary expansion: Given over complete dictionary \\(D\\in R^{n\\times l}\\) with \\(l>n\\), we want to a solution of
Under the assumption of \\(rank(D)=n\\), we know there are infinite solutions. Among these representations of \\(x\\), we are particularly interested in finding the most economical one, \\(\\theta^*\\) , that is the sparsest. Precisely, we need to solve:
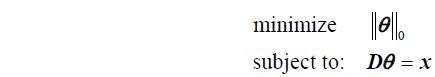 (1)
(1)
It turns out that (1) is a problem of combinatorial complexity: finding solution of (1) requires
enumerating subsets of the dictionary to identify the smallest subset that can represent signal \\(x\\), the
complexity of such a subset search grows exponentially with \\(l\\). An important result concerning sparse
signals and compressed sensing is that under certain conditions the sparsest solution of $D\\theta = x4 can be
obtained by solving the convex problem
 (2)
(2)
If the data involved are all real-valued, (2) is equivalent to a linear program (LP), if the data are
complex-valued, then (1.15) is essentially a second-order cone program (SOCP). Hence (2) can be
solved effectively using any good convex program solvers like SeDuMi.
Examples of Dictionaries:
-
\\(D=[I_n\\; C_n^T]\\), where \\(I_n\\) is the identity matrix of size \\(n\\times n\\), \\(C_n\\) is the 1-D DCT matrix of size \\(n\\times n\\).
-
\\(D=[I_n\\; W_n^T]\\), where \\(W_n\\) is a 1-D DWT matrix.
[Remark]Compared to traditional basis expansion, dictionary based sparse model is more sparse. Secondly, it should be noticed that proper choice of dictionary is important, e.g, \\(D=[I_n\\; C_n^T]\\) and \\(D=[I_n\\; W_n^T]\\) are very representive.
That is to say, the dictionary is always composed of traditional orthonormal matrix.
Some terminology:
1.Dictionary: matrix \\(D\\)
2.Atom: columns of \\(D\\).
3.Overcomplete: \\(n<l\\)
4. A signal is said to be approximately sparse if it differs from a “nearby” sparse signal by a small amount in magnitude.
5. A signal is said to be compressible, if there exists a basis in which the signal admits approximately sparse representation.