分治法-最近点对问题

Posted 2020-11-06 扶芥

设p1=(x1,y1),p2=(x2,y2)...pn=(xn,yn)是平面n上n个点构成的集合S，最近对问你就是找出集合S中距离最近的点对。

分支策略：

    （1）划分：将集合S分成两个子集S1和S2，根据平衡子问题原则，每个子集中大约有n/2个点，设集合S的最近点对是pi和pj(1<=i,j<=n）

                        则有以下三种情况 1.pi∈S1,pj∈S1

                                                       2.pi∈S1,pj∈S2

                                                       3.pi∈S2, pj∈S2

     （2）求解子问题：对于划分阶段的情况1和2可递归求解

                                   通过直线x=M（中位数）,将空间划为两部分,x<M和x>M分别求出左右最近点对距离，d1,d2,另d=min(d1,d2)

                                   则，只需考虑3,即x-d和x+d的区域之间的最近点对，按照Y坐标对区域内点进行排序，如果一个点对的距离

                                    小于d,他们一定在d*(2*d)的区域内。

                                   

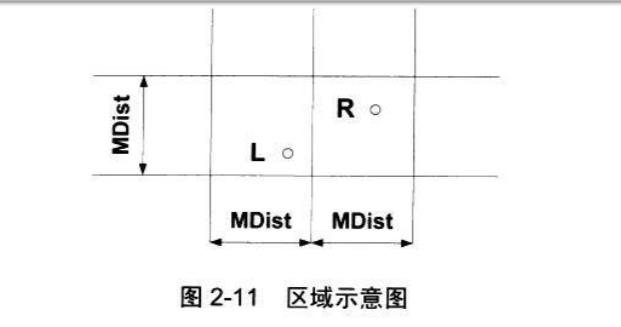
                                      对于算法 nearest_pair( S,left,right)

                                       1.预处理：对点集合S={(x1,y1),(x2,y2)......(xn,yn)}按照x坐标升序排列

                                        2.如果n=2，则返回连点之间距离

                                        3.m

                                           计算{(x1,y1),(x2,y2).....(xm,ym)}之间的最近距离

                                          计算{(xm,ym)(xm+1,ym+1)....(xn,yn)}之间的最近距离

                                         d=min(d1,d2)

                                        4.依次计算S[l...r]的最近点对（将集合按照y升序排列，考察y-s[m].y<d的点）

                                                l=min(i)| S[m]-S[i]<d

                                               r=max(i)| S[i]-S[m]<d

// 实验四.cpp: 定义控制台应用程序的入口点。

//最近对问题
//2018.4.18

#include "stdafx.h"
#include<iostream>
#include<stdio.h>
#include<stdio.h>
#include<algorithm>
#include<math.h>
#include<windows.h>
using namespace std;

struct point {
	double x;
	double y;
}P[100];
double distance(point p1, point p2) {
	return sqrt((p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y));
}
bool cmp1(point p1, point p2) {
	return p1.x < p2.x;
}
bool cmp2(point p1, point p2) {
	return p1.y < p2.y;
}
//蛮力法
double get_min(int n)
{
	double min = sqrt((P[0].x - P[1].x)*(P[0].x - P[1].x) + (P[0].y - P[1].y)*(P[0].y - P[1].y));
	for (int i = 0; i < n; i++) {
		for (int j = i + 1; j < n; j++) {
			double t = sqrt((P[i].x - P[j].x)*(P[i].x - P[j].x) + (P[i].y - P[j].y)*(P[i].y - P[j].y));
			if (min>t)
				min = t;
		}
	}
	return min;
}

//分治法
double nearest_pair(point S[],int left,int right) {
	cout << left << " " << right << endl;
	if (right-left == 1) {
		return distance(S[right], S[left]);
	}
	if (right - left == 2) {
		double d1 = distance(S[right], S[left]);
		double d2 = distance(S[right], S[right + 1]);
		double d3 = distance(S[right + 1], S[left]);
		d2 = min(d1, d2);
		d3 = min(d2, d3);
		return d3;
	}
	int m = (right+left) / 2;
	double d1 = nearest_pair(S,left, m);
	double d2 = nearest_pair(S, m+1,right);
	//sort(S+right, S+left, cmp2);
	double d = min(d1, d2);
	int l = left, r = right;
	while (S[l].x < S[m].x - d && l <= right);
		l++;
	while (S[r].x > S[m].x + d && r>=left)
		r++;
	sort(S + 1, S + r + 1, cmp2);
	double d3;
	for (int i = l; i <= r; i++) {
		for (int j = i + 1; j <= r; j++) {
			if (S[j].y - S[i].y >= d) {
				break;
			}
			else {
				d3 = distance(S[i], S[j]);
				if (d3 < d)
					d = d3;
			}
		}
	}
	return d;
}
int main()
{
	int n;
	cout << "Input n:";
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cout << "Input the " << i << "th number:";
		cin >> P[i].x >> P[i].y;
	}
	sort(P + 1, P + n+1, cmp1);
	for (int i = 1; i <= n; i++) {
		cout << P[i].x << " " << P[i].y << endl;
	}
	double m = get_min(n);
	cout << m << endl;
	double m2 = nearest_pair(P, 1, n);
	cout << m2 << endl;
	system("pause");
	return 0;
}