UVA_11178_Morley's_Theorem_(向量旋转+直线相交)

Posted 2020-07-11 晴歌。

描述

---

https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=23&page=show_problem&problem=2119

Morley定理:作三角形ABC每个内角的三等分线,相交形成三角形DEF,则三角形DEF是等边三角形.

给出三角形的三个顶点ABC的坐标,求出DEF的坐标.

 

11178 - Morley\'s Theorem

Time limit: 3.000 seconds

Morleys theorem states that that the lines
trisecting the angles of an arbitrary plane

triangle meet at the vertices of an equi-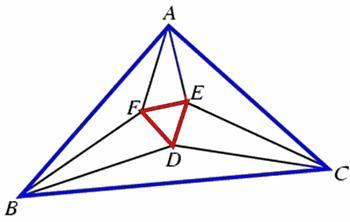
lateral triangle. For example in the figure
below the tri-sectors of angles A, B and C
has intersected and created an equilateral
triangle DEF.
Of course the theorem has various gen-
eralizations, in particular if all of the tri-
sectors are intersected one obtains four
other equilateral triangles. But in the
original theorem only tri-sectors nearest
to BC are allowed to intersect to get point
D, tri-sectors nearest to CA are allowed to intersect point E and tri-sectors nearest to AB are inter-
sected to get point F. Trisector like BD and CE are not allowed to intersect. So ultimately we get only
one equilateral triangle DEF. Now your task is to find the Cartesian coordinates of D, E and F given
the coordinates of A, B, and C.
Input
First line of the input file contains an integer N (0 < N < 5001) which denotes the number of
test cases to follow. Each of the next lines contain six integers X A , Y A , X B , Y B , X C , Y C . This six
integers actually indicates that the Cartesian coordinates of point A, B and C are (X A , Y A ),(X B , Y B )
and (X C , Y C ) respectively. You can assume that the area of triangle ABC is not equal to zero, 0 ≤
X A , Y A , X B , Y B , X C , Y C ≤ 1000 and the points A, B and C are in counter clockwise order.
Output
For each line of input you should produce one line of output. This line contains six floating point
numbers X D , Y D , X E , Y E , X F , Y F separated by a single space. These six floating-point actually means
that the Cartesian coordinates of D, E and F are (X D , Y D ),(X E , Y E ) ,(X F , Y F ) respectively. Errors
less than 10 −5 will be accepted.
Sample Input
2
1 1 2 2 1 2
0 0 100 0 50 50
Sample Output
1.316987 1.816987 1.183013 1.683013 1.366025 1.633975
56.698730 25.000000 43.301270 25.000000 50.000000 13.397460

 

分析

---

DEF三个点的求法是一样的,来看D:

将向量BC逆时针旋转(角ABC)/3,将向量CB顺时针旋转(角ACB)/3,分别得到了直线BD和直线CD的方向向量,再加上点B,C,可以写出直线BD和直线CD(参数方程),然后求两直线的交点即可.

 

注意:

1.get函数中的后两个参数不可颠倒,因为一边是逆时针转,另一边是顺时针转.

 

 

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 const double eps=1e-8;
 5 struct Point{
 6     double x,y;
 7     Point(double x=0,double y=0):x(x),y(y){}
 8 };
 9 typedef Point Vector;
10 
11 Vector operator + (Point a,Point b){ return Vector(a.x+b.x,a.y+b.y); }
12 Vector operator - (Point a,Point b){ return Vector(a.x-b.x,a.y-b.y); }
13 Vector operator * (Point a,double p){ return Vector(a.x*p,a.y*p); }
14 double dot(Vector a,Vector b){ return a.x*b.x+a.y*b.y; }//点积
15 double cross(Vector a,Vector b){ return a.x*b.y-a.y*b.x; }//叉积
16 double length(Vector a){ return sqrt(dot(a,a)); }//向量的模
17 double angle(Vector a,Vector b){ return acos(dot(a,b)/length(a)/length(b)); }//两向量夹角
18 Vector rotate(Vector a,double rad){ return Vector(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad)); }//将向量a逆时针旋转rad(弧度制)
19 Point get_line_intersection(Point P,Vector v,Point Q,Vector w){//求两直线交点(参数方程)
20     Vector u=P-Q;
21     double t=cross(w,u)/cross(v,w);
22     return P+v*t;
23 }
24 Point get(Point A,Point B,Point C){//分别算DEF三个点的函数
25     Vector v1=C-B;
26     double a1=angle(A-B,v1);
27     v1=rotate(v1,a1/3);
28     Vector v2=B-C;
29     double a2=angle(A-C,v2);
30     v2=rotate(v2,-a2/3);
31     return get_line_intersection(B,v1,C,v2);
32 }
33 int main(){
34     int n;
35     Point A,B,C,D,E,F;
36     scanf("%d",&n);
37     while(n--){
38         scanf("%lf%lf%lf%lf%lf%lf",&A.x,&A.y,&B.x,&B.y,&C.x,&C.y);
39         D=get(A,B,C);//这里B,C不能写反,因为一个是逆时针转,另一个时顺时针转
40         E=get(B,C,A);
41         F=get(C,A,B);
42         printf("%.6lf %.6lf %.6lf %.6lf %.6lf %.6lf\\n",D.x,D.y,E.x,E.y,F.x,F.y);
43     }
44     return 0;
45 }

View Code