如果有错误请指出, 谢谢
定义
竞赛图 : \\(\\binom n 2\\) 条边的有向图 (完全图)
定理 1
竞赛图强连通缩点后的DAG呈链状, 前面的所有点向后面的所有点连边
证明 : 考虑归纳, 逐连通块加入
目前有一条链, 插入一个新连通块x
如果x连向所有点, 放在链头
如果所有点连向x, 放在链尾
否则x的出边一定都在x的入边的后边 (否则成环)
找到分界点, 把x插在中间即可

定理 2
竞赛图的强连通块 存在一条哈密顿回路
证明 : 考虑归纳, 逐点加入
目前有一条链, 链上的每个强连通块都存在哈密顿回路
插入一个新点x, 只需证明新图中的强连通块都存在哈密顿回路即可
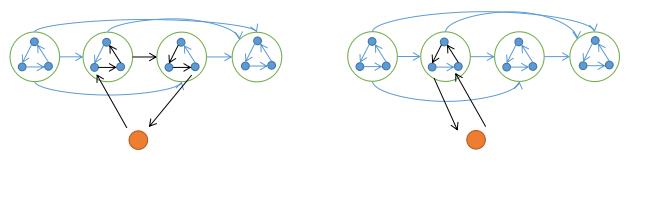
如果不产生新连通块, 就是定理 1 中讨论的情况, 否则一定存在一条x的出边在x入边左边, 随便找一对
如果是连到不同连通块, 见左图.
如果是同一连通块, 必定存在符合环的走向的相邻的一入一出, 见右图.
定理 3
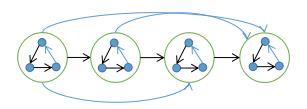
竞赛图存在一条 哈密顿路径
证明 : 如图示方法构造
引理
竞赛图里, 大小为 \\(n>1\\) 的强连通块中, 大小为 \\([3, n]\\) 的简单环均存在
证明 :
n=3成立, n$\\ge$4时只需证明存在大小为 \\(n-1\\) 的就好了
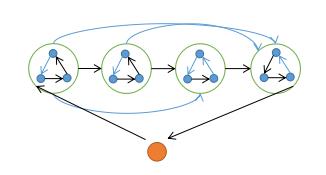
考虑从原图中提出一个点, 剩下的图是一条链, 提出来的点有出边指向链头, 有来自链尾的入边.
如果剩下的图只有一个强连通块, 那么大小为 \\(n-1\\) 的环已经存在了.
只需考虑至少两个强连通块的情况, 如图示方法构造
(在定理3构造的哈密顿路径中, 是一段环边一条链边这样走的, 将一段环边的起点/终点删掉.)
定理4
竞赛图判定定理 Landau\'s Theorem:
令\\(s_i\\)为第\\(i\\)个点的出度 (竞赛中获胜的积分)
对\\(s\\)排好序后, 若满足 \\(\\sum_{i=1}^k s_i\\ge \\binom k 2 且 \\sum s = \\binom n 2\\) , 定能构造出一种竞赛图, 反之不能
构造初始图:每个点向前面的所有点连边, 设此时得分序列为 \\(a\\), 这个序列在上述条件中取到等号
保持\\(\\sum_{i=1}^k a_i \\le \\sum_{i=1}^k s_i\\), 并不断调整图, 直到 \\(a=s\\)
未构造完成时, 开头必然是一段等于后面接着一个 \\(a_l\\lt s_l\\)
为了使按照后面的方法修改后的 \\(u\\) 仍有序, 我们找到最后一个 \\(a_l=a_u\\) 的 \\(u\\), 显然仍有 \\(a_u\\lt s_u\\)
因为总和固定, 必能在 \\(u\\) 后面找到 \\(a_v\\gt s_v\\), 找到第一个 \\(v\\)
此时 \\(a_u\\lt s_u\\le s_v\\lt a_v\\) , 即 \\(a_v\\ge a_u+2\\)
当存在 \\(\\exists v\\to u\\) 时, 直接翻转这条边
否则必然存在点 \\(p\\), 使得 \\(\\exists v\\to p,p\\to u\\), 将这条路径翻转
因为 \\(a_u\\lt s_u\\), \\(a_i\\le s_i, \\forall i \\in (u,v)\\), 不难证明修改后的序列仍然保持性质(任意a的前缀和都<=s的)
这样构造下去一定有解