洛谷 p1044 栈 Catalan（卡特兰数）经典题

Posted 2020-11-05 is_ok

题目链接：https://www.luogu.org/problemnew/show/P1044

转载于：https://www.luogu.org/blog/QiXingZhi/solution-p1044

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即pop（从栈顶弹出一个元素）和push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

 

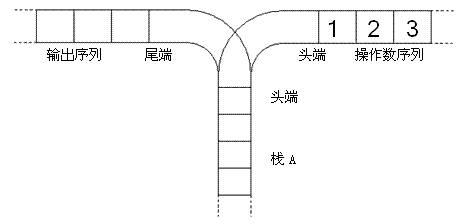
宁宁考虑的是这样一个问题：一个操作数序列，从1，2，一直到n（图示为1到3的情况），栈A的深度大于n。

现在可以进行两种操作，

1.将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的push操作）

2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的pop操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由1 2 3生成序列2 3 1的过程。

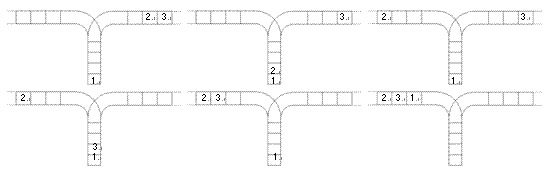
（原始状态如上图所示）

你的程序将对给定的n，计算并输出由操作数序列1，2，…，n经过操作可能得到的输出序列的总数。

输入输出格式

输入格式：

输入文件只含一个整数n（1≤n≤18）

输出格式：

输出文件只有一行，即可能输出序列的总数目

输入输出样例

输入样例#1： 

3

输出样例#1： 

5

解题思路：

本题的描述十分简单。n个数依次进栈，可随机出栈。求有几种可能。dfs可以解，但是递推仿佛好像如同看上去貌似更简单一些。解释一下原理：建立数组f。f[i]表示i个数的全部可能性。

f[0] = 1, f[1] = 1; //当然只有一个设 x 为当前出栈序列的最后一个，则x有n种取值由于x是最后一个出栈的，所以可以将已经出栈的数分成两部分

1. 比x小

2. 比x大

比x小的数有x-1个，所以这些数的全部出栈可能为f[x-1]，比x大的数有n-x个，所以这些数的全部出栈可能为f[n-x]，这两部分互相影响，所以一个x的取值能够得到的所有可能性为f[x-1] * f[n-x]

另外，由于x有n个取值，所以 ans = f[0]*f[n-1] + f[1]*f[n-2] + ... + f[n-1]*f[0];这，就是传说中的卡特兰数

附上代码：

#include <cstdio>

int n, f[30];
int main()
{
    //递推实现卡特兰数 
    scanf("%d", &n);
    f[0] = 1, f[1] = 1;
    for(int i=2; i<=n; i++)              
        for(int j=0; j<i; j++) 
            f[i] += f[j] * f[i-j-1];     //递推公式 
    printf("%d", f[n]);
    return 0;
}

2018-05-15