数据结构之平衡二叉树

Posted 2020-11-05 迷途纸鸢

首先资料参考于:https://www.cnblogs.com/PerkinsZhu/p/5824015.html

        二叉排序树集中了数组的查找优势以及链表的插入、删除优势，因此在数据结构中占有一定的地位。但在一定的情况下二叉排序树又有可能变为链表，例如插入从1~100的数，这时进行数据查找的效率就要降低。

为了解决二叉排序树这种左右子树深度不均匀的情况引入了一种*衡二叉树(AVLTree)任何一个节点的左右子树深度差不超过1.通过这个限定，阻止了二叉树的左右子树深度差较大的情况，维持了二叉树的稳定。

　　如何让二叉树的左右子树深度差不超过1呢？这就需要对节点进行旋转，也就是当某个节点的左右子树深度超过1时需要对这个节点进行旋转（旋转之后依旧是左子树小于节点小于右子树），重新调整树的结构。

例如：这两棵二叉树虽然结构不同，但是都是二叉排序树，所谓的旋转就是把左边的深度为3的树旋转为右边深度为2的二叉树。

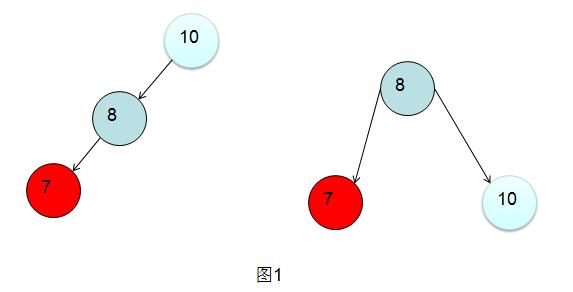
在*衡二叉树进行插入操作时遇到的不*衡情况有多种，但是这么多种情况都可以分解为一下四中基础情景：把它叫做：左左、左右、右右、右左。

在解释这四种情景之前需要先明白一个定义：最小不*衡节点—插入一个节点之后，距离这个插入节点最*的不*衡节点就是最小不*衡节点（如上图左树的10节点）。所有的旋转都是在最小不*衡节点的基础上进行的。

继续解释四种情景命名意义：左左：节点插入在最小不*衡节点的左子树的左子树上。     左右：节点插入在最小不*衡节点的左子树的右子树上面

　　　　　　　　　　　    　右：节点插入在最小不*衡树的右子树的右子树上面。　　　右左：节点插入在最小不*衡树的右子树的左子树上面。

下面就具体分析这四种情况：

　　左左：右旋

 

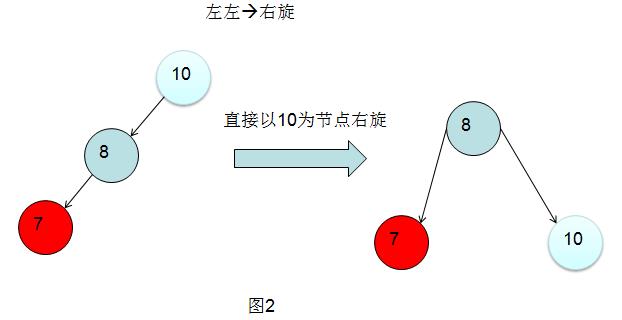
左左简单不用详解。

左右：先左旋再右旋

 

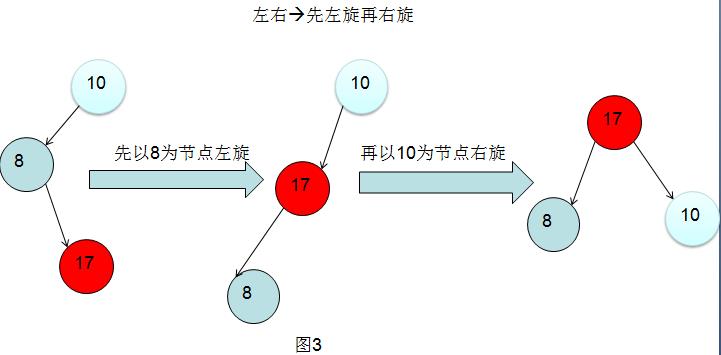
这里有人又有疑问了，上面的左左（图2）看明白了，可这里左右情景为什么要旋转两次呢？为什么先左旋，再右旋呢？

先别急，看看这种情况：（图4）

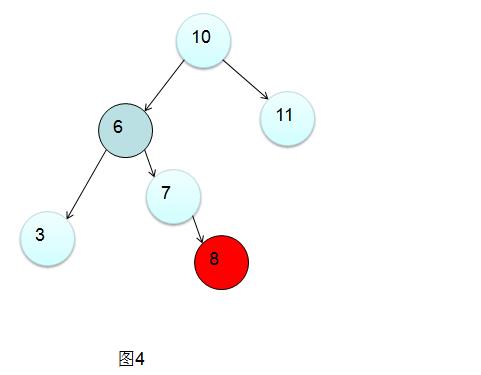
毫无疑问这也是 左右 情景（左左情景有很多种，图3演示的是最基础的情景，所有 的左左情景的旋转情况和图3都是一样的），那么该怎么旋转呢？

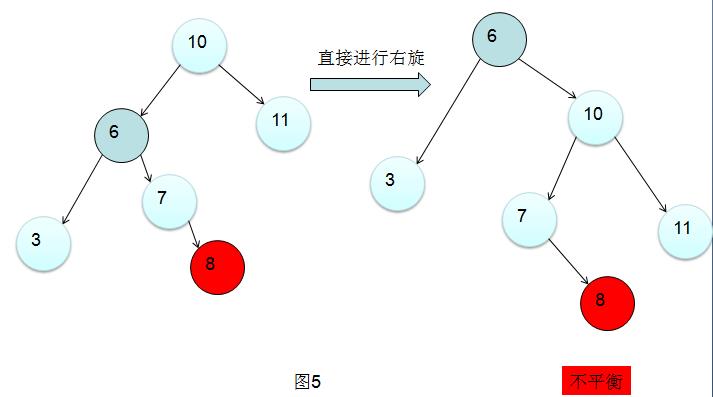
直接右旋不对吧？因为6节点的右子树（以根节点10为中心，靠*内部的子树）6-8经过旋转之后要充当10节点的左子树，这样会导致依旧不*衡。所以在这种左右情景下需要进行两次旋转，先把6的右子树降低高度，然后在进行右旋。即：

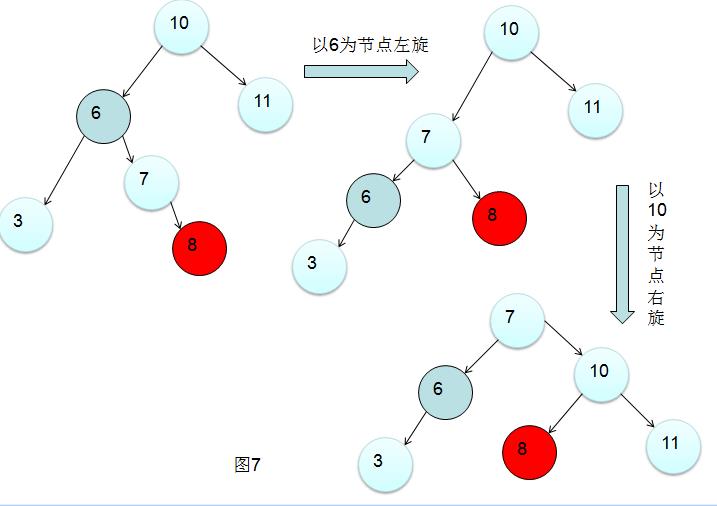
把图7 情景和图3的情景一样，这就是为什么 左右情景 需要先左旋再右旋的原因。

在这里可以记作：最小不*衡节点的左节点的内部（以根节点做对称轴，偏向对称轴的为内部。也就是以7为节点的子树）的子树高度高于外部子树的高度时需要进行两次旋转。

右右：左旋

 

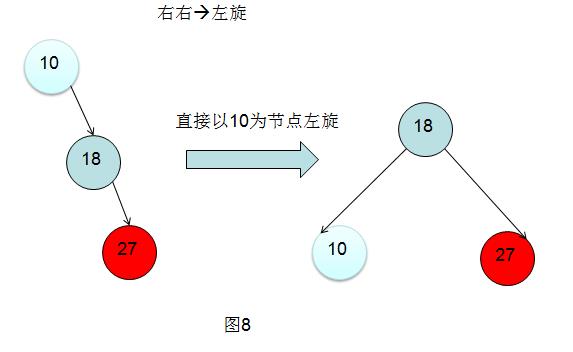
右右情景直接左旋即可。不在详解

右左：先右旋，再左旋

 

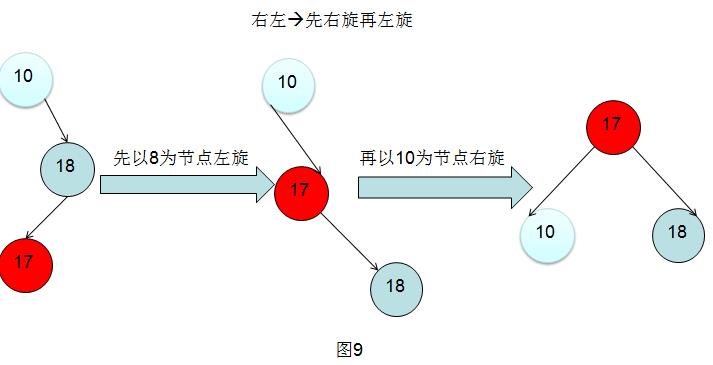
为什么这样旋转明白了吧？如同左右情景，考虑到图10的 右左情景

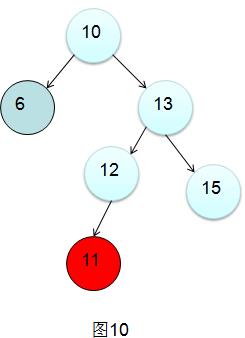
这种情景旋转如图11

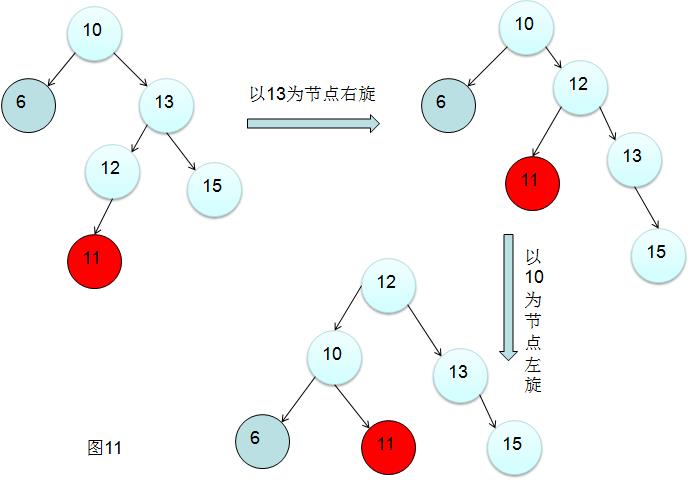
旋转的四种情景就这些了。需要说明的是，下面这两对情景旋转是一样的。

图12都是右左情景，具体看代码的旋转方法就明白了在第一次右旋的时候进行的操作。private Node<T> rotateSingleRight(Node<T> node)；

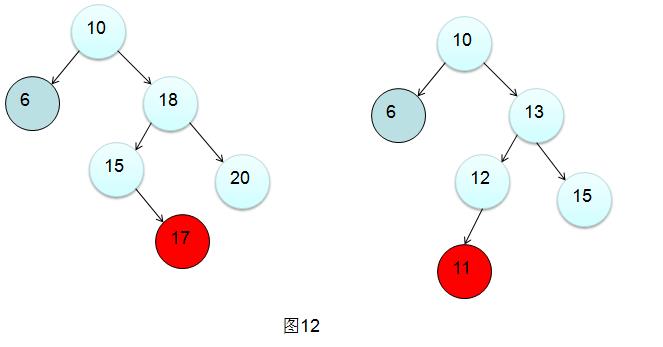
图13都是左右情景，第一次左旋见：private Node<T> rotateSingleLeft(Node<T> node)；

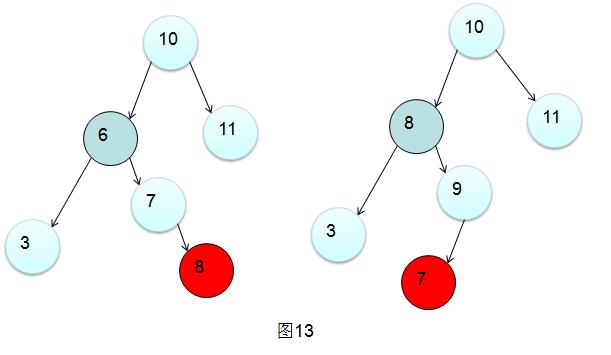
旋转情景弄明白之后就是怎么代码实现了，在实现代码之前需要考虑如何进行树高判断。这里就根据定义来，|左子树树高-右子树树高|<2。如果大于等于2则该节点就不在 *衡，需要进行旋转操作。因此在程序中节点中需要定义一个height属性来存储该节点的树高。

由于*衡二叉树的性质，二叉树的高度不会很高，程序使用递归进行数据插入查找不会造成栈溢出异常，所以程序采用递归操作进行插入查找。

*衡的判定策略是在进行递归回溯的时候依照回溯路径更新节点的树高，然后根据|左子树树高-右子树树高|<2来判定该节点是否失衡，进一步对是够旋转进行判定。

代码如下：

 

  1 #include "stdafx.h"
  2 #include<iostream>
  3 using namespace std;
  4 
  5 #define OK 1
  6 #define ERROR 0
  7 #define TRUE 1
  8 #define FALSE 0
  9 #define MAXSIZE 100
 10 typedef int Status;
 11 
 12 typedef struct BiTNode {
 13     int data;
 14     int bf;
 15     struct BiTNode *lchild, *rchild;
 16 }BiTNode,*BiTree;
 17 
 18 //对以p为根的二叉排序树作右旋处理，
 19 //处理之后p指向新的树根结点，即旋转处理之前的左子树的根结点
 20 void R_Rotate(BiTree *P)
 21 {
 22     BiTree L;
 23     L = (*P)->lchild;        //L指向P的左子树根结点
 24     (*P)->lchild = L->rchild;//L的右子树挂接为P的左子树
 25     L->rchild = (*P);
 26     *P = L;                  //P指向新的根结点
 27 }
 28 
 29 //对以P为根的二叉排序树作左旋处理,
 30 //处理之后P指向新的树根结点，即旋转处理之前的右子树的根结点0
 31 void L_Rotate(BiTree *P)
 32 {
 33     BiTree R;
 34     R = (*P)->rchild;        //R指向P的右子树根结点
 35     (*P)->rchild = R->lchild;//R的左子树挂接为P的右子树
 36     R->lchild = (*P);        //P指向新的根结点
 37     *P = R;
 38 }
 39 
 40 #define LH +1                //左高
 41 #define EH 0                 //等高
 42 #define RH -1                //右高
 43 
 44 //对以指针T所指结点为根的二叉树作左*衡旋转处理
 45 //本算法结束时，指针T指向新的根结点
 46 void LeftBalance(BiTree *T)
 47 {
 48     BiTree L, Lr;
 49     L = (*T)->lchild;        //L指向T的左子树根结点 
 50     switch (L->bf)
 51     {                        //检查T的左子树的*衡度，并作相应*衡处理
 52     case LH:                 //新结点插入在T的左孩子的左子树上，要作单右旋处理
 53         (*T)->bf = L->bf = EH;
 54         R_Rotate(T);
 55         break;
 56     case RH:                 //新结点插入在T的左孩子的右子树上，要作双旋处理
 57         Lr = L->rchild;// Lr指向T的左孩子的右子树根
 58         switch (Lr->bf)
 59         {                    //修改T及其左孩子的*衡因子
 60         case LH:(*T)->bf = RH;
 61             L->bf = EH;
 62             break;
 63         case EH:(*T)->bf = L->bf = EH;
 64             break;
 65         case RH:(*T)->bf = EH;
 66             L->bf = LH;
 67             break;
 68         }
 69         Lr->bf = EH;
 70         L_Rotate(&(*T)->lchild);//对T的左子树作左旋*衡处理 
 71         R_Rotate(T);         //对T作右旋*衡处理
 72     }
 73 }
 74 
 75 //对以指针T所指结点为根的二叉树作右*衡旋转处理
 76 //本算法结束时，指针T指向新的根结点
 77 void RightBalance(BiTree *T)
 78 {
 79     BiTree R, Rl;
 80     R = (*T)->rchild;        //R指向T的右子树根结点
 81     switch (R->bf)
 82     {                        //检查T的右子树的*衡度，并作相应*衡处理
 83     case RH:                 //新结点插入在T的右孩子的右子树上，要作单左旋处理
 84         (*T)->bf = R->bf = EH;
 85         L_Rotate(T);
 86         break;
 87     case LH:                 //新结点插入在T的右孩子的左子树上，要作双旋处理
 88         Rl = R->lchild;      //Rl指向T的右孩子的左子树根
 89         switch (Rl->bf)
 90         {                    //修改T及其右孩子的*衡因子
 91         case RH: (*T)->bf = LH;
 92             R->bf = EH;
 93             break;
 94         case EH: (*T)->bf = R->bf = EH;
 95             break;
 96         case LH: (*T)->bf = EH;
 97             R->bf = RH;
 98             break;
 99         }
100         Rl->bf = EH;
101         R_Rotate(&(*T)->rchild);//对T的右子树作右旋*衡处理
102         L_Rotate(T);         //对T作左旋*衡处理
103     }
104 }
105 
106 //若在*衡的二叉排序树T中不存在和e有相同关键字的结点，则插入一个
107 //数据元素为e的新结点，并返回1，否则返回0。若因插入而使二叉排序树
108 //失去*衡，则作*衡旋转处理，布尔变量taller反映T长高与否。
109 Status InsertAVL(BiTree *T, int e, Status *taller)
110 {
111     if (!*T)
112     {                        //插入新结点，树“长高”，置taller为TRUE
113         *T = new BiTNode;
114         (*T)->data = e; 
115         (*T)->lchild = (*T)->rchild = NULL; 
116         (*T)->bf = EH;
117         *taller = TRUE;
118     }
119     else
120     {
121         if (e == (*T)->data)
122         {                    //树中已存在和e有相同关键字的结点则不再插入
123             *taller = FALSE; return FALSE;
124         }
125         if (e<(*T)->data)
126         {                    //应继续在T的左子树中进行搜索
127             if (!InsertAVL(&(*T)->lchild, e, taller)) //未插入
128                 return FALSE;
129             if (taller)      //已插入到T的左子树中且左子树“长高”
130                 switch ((*T)->bf) //检查T的*衡度 */
131                 {
132                 case LH:     //原本左子树比右子树高，需要作左*衡处理
133                     LeftBalance(T);    *taller = FALSE; break;
134                 case EH:     //原本左、右子树等高，现因左子树增高而使树增高
135                     (*T)->bf = LH; *taller = TRUE; break;
136                 case RH:     //原本右子树比左子树高，现左、右子树等高 
137                     (*T)->bf = EH; *taller = FALSE; break;
138                 }
139         }
140         else
141         {                    //应继续在T的右子树中进行搜索
142             if (!InsertAVL(&(*T)->rchild, e, taller)) //未插入
143                 return FALSE;
144             if (*taller)     //已插入到T的右子树且右子树“长高
145                 switch ((*T)->bf) //检查T的*衡度
146                 {
147                 case LH:     //原本左子树比右子树高，现左、右子树等高
148                     (*T)->bf = EH; 
149                     *taller = FALSE;    
150                     break;
151                 case EH:     //原本左、右子树等高，现因右子树增高而使树增高
152                     (*T)->bf = RH; 
153                     *taller = TRUE; 
154                     break;
155                 case RH:     //原本右子树比左子树高，需要作右*衡处理
156                     RightBalance(T); 
157                     *taller = FALSE; 
158                     break;
159                 }
160         }
161     }
162     return TRUE;
163 }
164 
165 int main()
166 {
167     int i;
168     int a[10] = { 3,2,1,4,5,6,7,10,9,8 };
169     BiTree T = NULL;
170     Status taller;
171     for (i = 0; i<10; i++)
172     {
173         InsertAVL(&T, a[i], &taller);
174     }
175     printf("本样例建议断点跟踪查看*衡二叉树结构");
176     return 0;
177 }