麦克斯韦方程组

Posted 2020-11-05 帅气一匹马

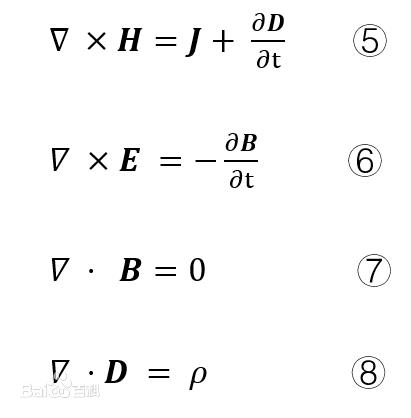
E和H类比，B和D类比。H线积分就是F磁动势，E线积分就是φ 电动势。

B和D 一个是磁密度 一个是电流密度（位移电流）。

B=μH，μ是磁导率 ; D=εE,其实介电常数从某种意义上和电导率有关的。

D是电位移矢量，H是磁场强度；它们都是考虑了介质之后的情况。一个是电介质，一个是磁媒质。

 

---

 

1. 力、能、场、势

经典物理研究的一个重要对象就是力force。比如牛顿力学的核心就是 这个公式，剩下的什么平抛圆周简谐运动都可以用这货加上微积分推出来。但是力有一点不好，它是个向量vector（既有大小又有方向），所以即便是简单的受力分析，想解出运动方程却难得要死。很多时候，从能量的角度出发反而问题会变得简单很多。能量energy说到底就是力在空间上的积分（能量=功=力×距离），所以和力是有紧密联系的，而且能量是个标量scalar，加减乘除十分方便。分析力学中的拉格朗日力学和哈密顿力学就绕开了力，从能量出发，算运动方程比牛顿力学要简便得多。

在电磁学里，我们通过力定义出了场field的概念。我们注意到洛仑兹力总有着 的形式，具体不谈，单看这个公式就会发现力和电荷（或电荷×速度）程正比。那么我们便可以刨去电荷（或电荷×速度）的部分，仅仅看剩下的这个“系数”有着怎样的动力学性质。也就是说，场是某种遍布在空间中的东西，当电荷置于场中时便会受力。具体到两个电荷间的库仑力的例子，就可以理解为一个电荷制造了电场，而另一个电荷在这个电场中受到了力，反之亦然。类似地我们也可以对能量做相同的事情，刨去能量中的电荷（或电荷×速度），剩下的部分便是势potential。

一张图表明关系：
　　　　积分
　　力－－－＞能
　　｜　　　　｜
　　场＜－－－势
　　　　微分

具体需要指出，这里的电场（标为 ）和磁场（标为 ）都是向量场，也就是说空间中每一个点都对应着一个向量。如果我们把xyz三个分量分开来看的话，这就是三个标量场。而能量和势是标量（电磁学中的势其实并不是标量，原因马上揭晓），放到空间中也就是一个标量场。在力/场和能量/势之间互相转化的时候，我们是在3<->1个标量场之间转化，必然有一些信息是丢掉了的。怎么办？

一个显而易见的答案是“保守力场”conservative force field。在这样一个场中，能量（做功）不取决于你选择什么样的路径。打个比方，你爬一座山，无论选择什么路径，只要起点和终点一样，那么垂直方向上的差别都是一样的，做的功也一样多。在这种情况下，我们对力场有了诸多限制，也就是说，我假如知道了一个保守力场的x一个分量，那么另两个分量yz就随之确定了，我没得选（自由度其实只有一个标量场）。有了保守力场这样的额外限制，向量场F（3个标量场）和（1个）标量场V之间的转化便不会失去信息了。具体而言，二者关系可以写作 。这里不说具体细节，你只要知道 是一种固定的、把一个标量场变成三个标量场的算法就可以了（叫做算符operator）。

那么我们想问，电场和磁场是不是保守力场呢？很不幸，不是。在静电学中，静止的电场是保守的，但在电动力学中，只要有变化的电场和磁场，电场就不是一个保守力场了；而磁场从来都不是保守力场。这也就是说明，在电磁学中，我们很少涉及能量这个概念，因为它不能完整地描述一个电磁场。我们更多时候只关注“场”这个概念，尽管因此我们不得不涉足很多向量微积分，但我们没有办法，这是不让信息丢掉的唯一办法。那么，既然势也是标量，它是否也是一个没什么用的概念呢？恰恰相反，在电动力学中我们定义出了“向量势”vector potential，以保留额外的自由度。后面我会更具体地谈到这一点。

总而言之，我想说明一点，那就是电磁学的主要研究对象是电场和磁场，而麦克斯韦方程组就是描述电场和磁场的方程。势（包括电势和磁向量势）也是有用的概念，而且不像引力势是一个标量，在电磁学中势不得不变成一个向量。

 

---

 

 

 

梯度的旋度一定为0。这是可以想象的，梯度指的是上坡的方向，而如果它有旋度，就意味着它们的指向可以形成的一个环，在这个环上可以一直上坡。这就像彭罗斯楼梯，是不可能的情形。

 

旋度的散度一定为0。如果旋度有散度，就意味着在某个球上散度都在往球外指，也就意味着在球上每个点这个场都是逆时针旋转的。

梯度的散度，叫“拉普拉斯算符”Laplacian。

 

---

 

电势、磁向量势

我们可以把任意一个向量场 拆成两部分，第一部分只有散度没有旋度，第二部分只有旋度没有散度，然后 就是这两个部分加在一起（这就是亥姆霍茲定理Helmholtz theorem）。比如静电场没有旋度，那它就只有第一部分、第二部分就为0；磁场没有散度，则只有第二部分、第一部分为0。

其中负号不重要只是个习惯， 是个标量场叫做“标量势”或者就简称“势”potential， 是个向量场叫做“向量势”vector potential。叫它们“势”的原因是我们对它微分（梯度或旋度）就可以得到我们想要的场，符合我们一般的习惯。

在引力场和静电场这种保守力场中，旋度是0，于是第二部分 也为0，这就是我们以前没见过“向量势” 的原因。但是现在我们看到，在讨论更一般的场的时候，我们必须加入这个向量势 ，来描述这个场的旋度。

在电磁学中，我们专门地把电场 的标量势 叫做“电势”electric potential，把磁场 的向量势 叫做“磁向量势”magnetic vector potential或简称“磁势”。注意到磁场没有标量势，而电场的向量势可以用磁向量势表达出来（利用法拉第定律），所以我们省了一个变量。那么根据这个定义，电场和磁场就变成了：

---

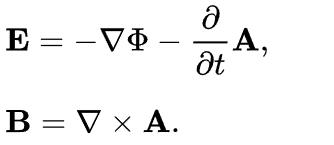
电场和磁场已经够绕的了，为什么要引入这么两个新的场？还加入了好多新的微分？什么梯度旋度看得我头都晕了！现在我来列举好处：

1. 减少了自由度。电场 和磁场 都是向量场，也就意味着总共有3+3=6个标量场的自由度。而电势 和磁势 一个是标量场一个是向量场，只有1+3=4个自由度。这就意味着用电场和磁场来描述电磁场的状态时，有冗余的信息（用电势和磁势来描述的话，也会有冗余的信息，没办法，但能减少一些自由度总是好的）。

2. 减少了麦克斯韦方程组的方程数量。电场和磁场有更多的自由度，也就意味着必须要有更多的方程来约束它们。事实上，麦克斯韦方程组里的法拉第定律和高斯磁定律正是用来约束电磁场的自由度的，因为你看，它们俩不涉及来源（电荷与电流），只是说明了电场和磁场之间的相互关系，换句话说，就是恒等式identities。而使用电势和磁势之后，电场和磁场的定义直接保证了这两个恒等式必然成立，我们便可以把它们踢出麦克斯韦方程组，从而只剩下两个方程。

3. 可以组成有四个分量的四维向量four vectors，即电势+三个磁势。对相对论比较熟悉的同学可能知道，电磁学和相对论是完全相容的，而相对论里全都是四维向量（时间+三个空间、能量+三个动量、如此等等）。引入这样的形式可以让相对论和电动力学结合得更加紧密。

 

作者：孙研
链接：https://www.zhihu.com/question/36766702/answer/70426471
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。