POJ-2992 Divisors---组合数求因子数目

Posted 2020-11-05 努力努力再努力x

题目链接：

https://cn.vjudge.net/problem/POJ-2992

题目大意：

给出组合数C_n^k，求出其因子个数，其中n，k不大于431，组合数的值在long long范围内

解题思路：

由于只有431种阶乘，先预处理431中素数，再预处理出每一个阶乘里面所含的素因子的指数，然后对于组合数，直接用素因子指数相减即可。

求出的质因子指数，就可以用定理直接求因子个数。

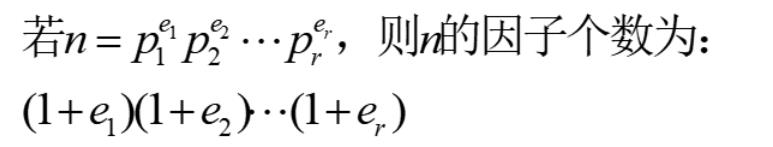
 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 using namespace std;
 5 typedef long long ll;
 6 bool not_prime[1000];
 7 int prime[200], tot;
 8 void sieve(int n)
 9 {
10     for(int i = 2; i <= n; i++)
11     if(!not_prime[i])
12     {
13         prime[tot++] = i;
14         for(int j = i * 2; j <= n; j += i)
15             not_prime[j] = 1;
16     }
17 }
18 int a[500][100];//a[i][j]表示i的阶乘中素数prime[j]的指数
19 void init(int n)
20 {
21     for(int i = 2; i <= n; i++)
22     {
23         for(int j = 0; j < tot && prime[j] <= n; j++)
24         {
25             if(i % prime[j] == 0)
26             {
27                 int t = i;
28                 while(t % prime[j] == 0)
29                 {
30                     t /= prime[j];
31                     a[i][j]++;
32                 }
33             }
34             a[i][j] += a[i - 1][j];
35         }
36     }
37     /*for(int i = 1; i <= 50; i++)
38     {
39         for(int j = 0; j < tot; j++)
40         {
41             if(a[i][j])
42             {
43                 printf("%d %d %d\\n", i, prime[j], a[i][j]);
44             }
45         }
46     }*/
47 }
48 int main()
49 {
50     sieve(431);
51     init(431);
52     int n, k;
53     while(scanf("%d%d", &n, &k) != EOF)
54     {
55         int ant[100];
56         for(int i = 0; i < tot; i++)
57             ant[i] = a[n][i] - a[k][i] - a[n - k][i];
58         ll ans = 1;
59         for(int i = 0; i < tot; i++)
60             ans *= (ant[i] + 1);
61         printf("%lld\\n", ans);
62     }
63     return 0;
64 }