矩阵快速幂
Posted 白雪儿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵快速幂相关的知识,希望对你有一定的参考价值。
写在前面
快速幂思想:
降低时间复杂度,使用尽量少的相乘次数。
例如:q^w化为(q*q)^(w/2) 。注意:当w为奇数的时候,我们要把(q*q)^(w/2)乘以q,理由是符号“/”是整除。所以在快速幂中乘积的底数是q*q,不是q了。
展示实例
问题描述
给定一个N阶矩阵A,输出A的M次幂(M是非负整数)
例如:
A =
1 2
3 4
A的2次幂
7 10
15 22
输入格式
第一行是一个正整数N、M(1<=N<=30, 0<=M<=5),表示矩阵A的阶数和要求的幂数。接下来N行,每行N个绝对值不超过10的非负整数,描述矩阵A的值。
输出格式
样例输入
2 2
1 2
3 4
样例输出
7 10
15 22
思路解析
用矩阵快速幂优化时间复杂度。
代码详解
1 #include<stdio.h>
2 #include<string.h>
3 using namespace std;
4 struct M
5 {
6 int num[35][35];
7 M()
8 {
9 memset(num,0,sizeof(num));
10 }
11 } a,e;
12 int m;
13 M chengji(M a,M b)//两个矩阵乘积结果得到一个矩阵
14 {
15 M q;
16 for(int i=0; i<m; i++)
17 {
18 for(int j=0; j<m; j++)
19 {
20 for(int k=0; k<m; k++)
21 {
22 q.num[i][j]+=(a.num[i][k]*b.num[k][j]);
23 }
24 }
25 }
26 return q;
27 }
28 M mulPower(M c,int n) //矩阵快速幂
29 {
30 M b=c,ans=e;
31 while(n)
32 {
33 if(n&1)
34 {
35 ans=chengji(ans,b);
36 }
37 b=chengji(b,b);
38 n>>=1;
39 }
40 return ans;
41 }
42 int main()
43 {
44 int n;
45 scanf("%d %d",&m,&n);
46 for(int i=0; i<m; i++)
47 {
48 e.num[i][i]=1;
49 for(int j=0; j<m; j++)
50 {
51 scanf("%d",&a.num[i][j]);
52 }
53 }
54 M x = mulPower(a,n);
55 for(int i=0; i<m; i++)
56 {
57 for(int j=0; j<m; j++)
58 {
59 printf("%d ",x.num[i][j]);
60 }
61 printf("\\n");
62 }
63 return 0;
64 }
总结提升
矩阵快速幂的实例:
斐波那契数列。它的递推公式为:F[n] = F[n-1] + F[n-2] 。 可以用矩阵表示:
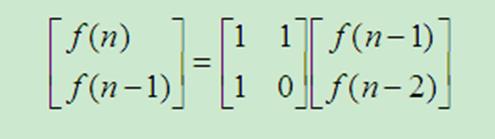
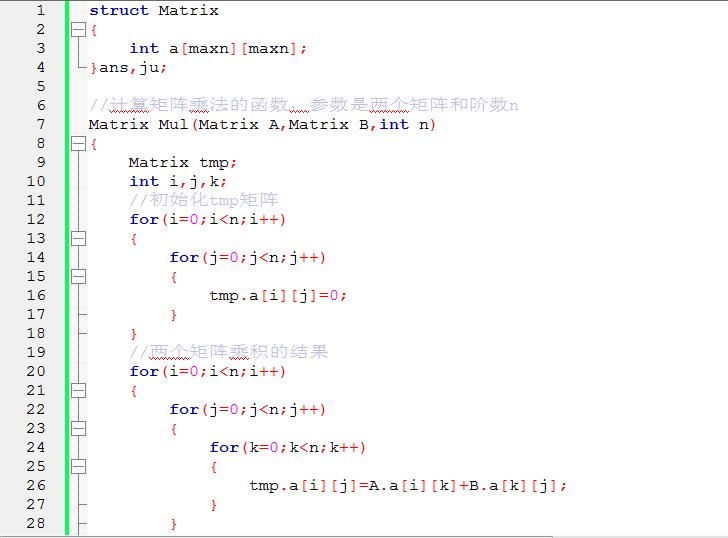
矩阵快速幂算法实现:

1 struct Matrix
2 {
3 int a[maxn][maxn];
4 }ans,ju;
5
6 //计算矩阵乘法的函数,参数是两个矩阵和阶数n
7 Matrix Mul(Matrix A,Matrix B,int n)
8 {
9 Matrix tmp;
10 int i,j,k;
11 //初始化tmp矩阵
12 for(i=0;i<n;i++)
13 {
14 for(j=0;j<n;j++)
15 {
16 tmp.a[i][j]=0;
17 }
18 }
19 //两个矩阵乘积的结果
20 for(i=0;i<n;i++)
21 {
22 for(j=0;j<n;j++)
23 {
24 for(k=0;k<n;k++)
25 {
26 tmp.a[i][j]=A.a[i][k]+B.a[k][j];
27 }
28 }
29 }
30 return tmp;
31 }
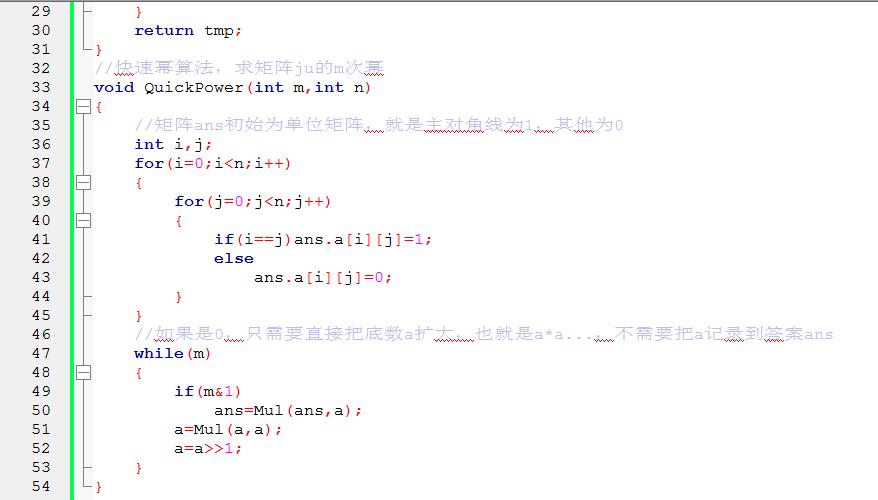
32 //快速幂算法,求矩阵ju的m次幂
33 void QuickPower(int m,int n)
34 {
35 //矩阵ans初始为单位矩阵,就是主对角线为1,其他为0
36 int i,j;
37 for(i=0;i<n;i++)
38 {
39 for(j=0;j<n;j++)
40 {
41 if(i==j)ans.a[i][j]=1;
42 else
43 ans.a[i][j]=0;
44 }
45 }
46 //如果是0,只需要直接把底数a扩大,也就是a*a...,不需要把a记录到答案ans
47 while(m)
48 {
49 if(m&1)
50 ans=Mul(ans,a);
51 a=Mul(a,a);
52 a=a>>1;
53 }
54 }
#include<stdio.h>
#include<string.h>
using namespace std;
struct M
{
int num[35][35];
M()
{
memset(num,0,sizeof(num));
}
} a,e;
int m;
M chengji(M a,M b)//两个矩阵乘积结果得到一个矩阵
{
M q;
for(int i=0; i<m; i++)
{
for(int j=0; j<m; j++)
{
for(int k=0; k<m; k++)
{
q.num[i][j]+=(a.num[i][k]*b.num[k][j]);
}
}
}
return q;
}
M mulPower(M c,int n) //矩阵快速幂
{
M b=c,ans=e;
while(n)
{
if(n&1)
{
ans=chengji(ans,b);
}
b=chengji(b,b);
n>>=1;
}
return ans;
}
int main()
{
int n;
scanf("%d %d",&m,&n);
for(int i=0; i<m; i++)
{
e.num[i][i]=1;
for(int j=0; j<m; j++)
{
scanf("%d",&a.num[i][j]);
}
}
M x = mulPower(a,n);
for(int i=0; i<m; i++)
{
for(int j=0; j<m; j++)
{
printf("%d ",x.num[i][j]);
}
printf("\\n");
}
return 0;
}
以上是关于矩阵快速幂的主要内容,如果未能解决你的问题,请参考以下文章