机器学习_贝叶斯算法
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习_贝叶斯算法相关的知识,希望对你有一定的参考价值。

















朴素贝叶斯
一、概述
1. 条件概率公式
2. 贝叶斯推断
3. 嫁?还是不嫁?这是一个问题……
二、朴素贝叶斯种类
1. GaussianNB
2. MultinomialNB
3. BernoulliNB
三、朴素贝叶斯之鸢尾花数据实验
1. 导入数据集
2. 切分训练集和测试集
3. 构建高斯朴素贝叶斯分类器
4. 测试模型预测效果
四、使用朴素贝叶斯进行文档分类
1. 构建词向量
2. 朴素贝叶斯分类器训练函数
3. 测试朴素贝叶斯分类器
4. 朴素贝叶斯改进之拉普拉斯平滑
一、概述
贝叶斯分类算法是统计学的一种概率分类方法,朴素贝叶斯分类是贝叶斯分类中最简单的一种。其分类原理就是利用贝叶斯公式根据某特征的先验概率计算出其后验概率,然后选择具有最大后验概率的类作为该特征所属的类。之所以称之为”朴素”,是因为贝叶斯分类只做最原始、最简单的假设:所有的特征之间是统计独立的。
假设某样本X有a1,a2,...an个属性,那么有P(X)=P(a1,a2,...an)=P(a1)*P(a2)*...P(an)。满足这样的公式就说明特征统计独立。
1. 条件概率公式
条件概率(Condittional probability),就是指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。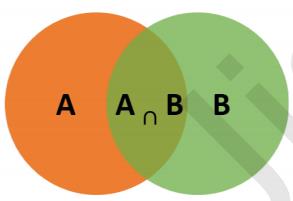
根据文氏图可知:在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。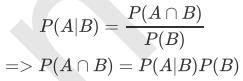
同理可得: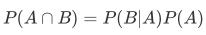
所以: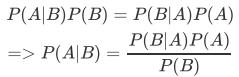
接着看全概率公式,如果事件A1,A2,A3,...,An构成一个完备事件且都有正概率,那么对于任意一个事件B则有: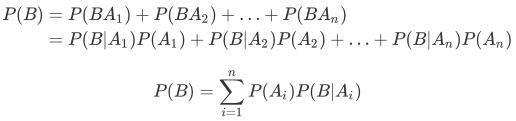
2. 贝叶斯推断
根据条件概率和全概率公式,可以得到贝叶斯公式如下: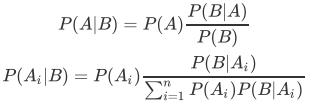
P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为"可能性函数"(Likely hood),这是一个调整因子,使得预估概率更接近真实概率。
所以条件件概率可以理解为:后验概率 = 先验概率 * 调整因子
如果"可能性函数">1,意味着"先验概率"被增强,事件A的发生的可能性变大;
如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;
如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
3. 嫁?还是不嫁?这是一个问题……
为了加深对朴素贝叶斯的理解,我们举个例子: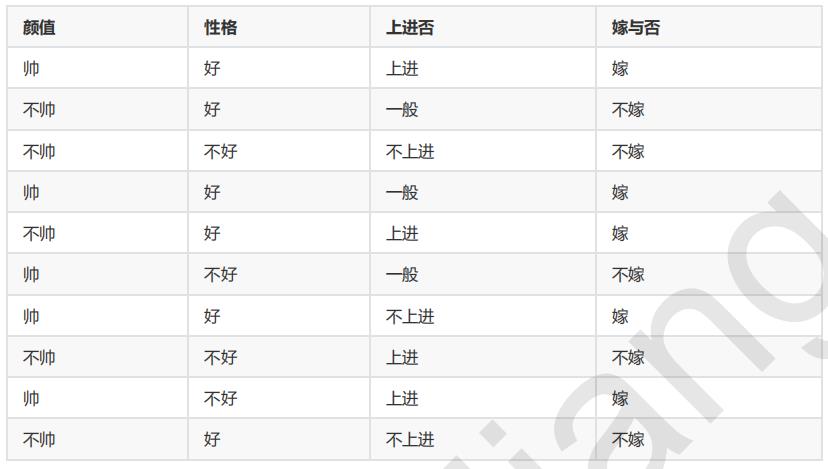
假如某男(帅,性格不好,不上进)向女生求婚,该女生嫁还是不嫁?
根据贝叶斯公式: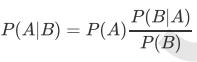
转换成分类任务的表达式: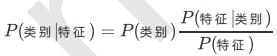
我们这个例子,按照朴素贝叶斯的求解,可以转换为计算 嫁 帅 性 格 不 好 不 上 进 和 不 嫁 帅 性 格 不 好 不 上 进 ,最终选择嫁与不嫁的答案。
根据贝叶斯公式可知: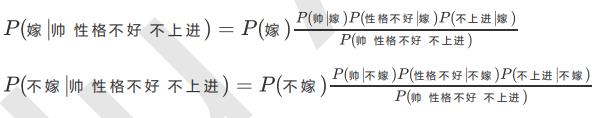
分母的计算用到的是全概率公式: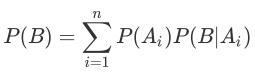
所以:
由上表可以得出:
P(嫁)= 5/10 = 1/2
P(不嫁)= 5/10 = 1/2
P(帅|嫁) * P(性格不好|嫁) * P(不上进|嫁)= 4/5 * 1/5 * 1/5
P(帅|不嫁) * P(性格不好|不嫁) * P(不上进|不嫁) = 1/5 * 3/5 * 2/5
对于类别“嫁”的贝叶斯分子为:
P(嫁) * P(帅|嫁) * P(性格不好|嫁) * P(不上进|嫁) = 1/2 * 4/5 * 1/5 * 1/5 = 2/125
对于类别“不嫁”的贝叶斯分子为:
P(不嫁) * P(帅|不嫁) * P(性格不好|不嫁) * P(不上进|不嫁) = 1/2 * 1/5 * 3/5 * 2/5 = 3/125
所以最终结果为:
P(嫁|帅\\ 性格不好\\ 不上进) = (2/125) / (2/125 + 3/125) = 40%
P(不嫁|帅\\ 性格不好\\ 不上进) = (3/125) / (2/125 + 3/125) = 60%
60% > 40%,该女生选择不嫁。
二、朴素贝叶斯种类
在scikit-learn中,一共有3个朴素贝叶斯的分类算法。分别是GaussianNB,MultinomialNB和BernoulliNB。
1. GaussianNB
GaussianNB就是先验为高斯分布(正态分布)的朴素贝叶斯,假设每个标签的数据都服从简单的正态分布。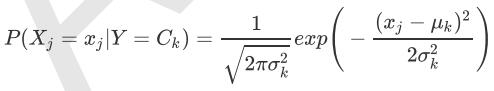
其中 Ck为Y的第k类类别。μk和σk2为需要从训练集估计的值。
这里,用scikit-learn简单实现一下GaussianNB。
#导入包 import pandas as pd from sklearn.naive_bayes import GaussianNB#导入高斯分布朴素贝叶斯包 from sklearn.model_selection import train_test_split#导入训练集和测试集划分的包 from sklearn.metrics import accuracy_score#导入计算准确率的包
#导入数据集 from sklearn import datasets iris=datasets.load_iris()
iris
结果:

{\'data\': array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2],
[4.6, 3.1, 1.5, 0.2],
[5. , 3.6, 1.4, 0.2],
[5.4, 3.9, 1.7, 0.4],
[4.6, 3.4, 1.4, 0.3],
[5. , 3.4, 1.5, 0.2],
[4.4, 2.9, 1.4, 0.2],
[4.9, 3.1, 1.5, 0.1],
[5.4, 3.7, 1.5, 0.2],
[4.8, 3.4, 1.6, 0.2],
[4.8, 3. , 1.4, 0.1],
[4.3, 3. , 1.1, 0.1],
[5.8, 4. , 1.2, 0.2],
[5.7, 4.4, 1.5, 0.4],
[5.4, 3.9, 1.3, 0.4],
[5.1, 3.5, 1.4, 0.3],
[5.7, 3.8, 1.7, 0.3],
[5.1, 3.8, 1.5, 0.3],
[5.4, 3.4, 1.7, 0.2],
[5.1, 3.7, 1.5, 0.4],
[4.6, 3.6, 1. , 0.2],
[5.1, 3.3, 1.7, 0.5],
[4.8, 3.4, 1.9, 0.2],
[5. , 3. , 1.6, 0.2],
[5. , 3.4, 1.6, 0.4],
[5.2, 3.5, 1.5, 0.2],
[5.2, 3.4, 1.4, 0.2],
[4.7, 3.2, 1.6, 0.2],
[4.8, 3.1, 1.6, 0.2],
[5.4, 3.4, 1.5, 0.4],
[5.2, 4.1, 1.5, 0.1],
[5.5, 4.2, 1.4, 0.2],
[4.9, 3.1, 1.5, 0.1],
[5. , 3.2, 1.2, 0.2],
[5.5, 3.5, 1.3, 0.2],
[4.9, 3.1, 1.5, 0.1],
[4.4, 3. , 1.3, 0.2],
[5.1, 3.4, 1.5, 0.2],
[5. , 3.5, 1.3, 0.3],
[4.5, 2.3, 1.3, 0.3],
[4.4, 3.2, 1.3, 0.2],
[5. , 3.5, 1.6, 0.6],
[5.1, 3.8, 1.9, 0.4],
[4.8, 3. , 1.4, 0.3],
[5.1, 3.8, 1.6, 0.2],
[4.6, 3.2, 1.4, 0.2],
[5.3, 3.7, 1.5, 0.2],
[5. , 3.3, 1.4, 0.2],
[7. , 3.2, 4.7, 1.4],
[6.4, 3.2, 4.5, 1.5],
[6.9, 3.1, 4.9, 1.5],
[5.5, 2.3, 4. , 1.3],
[6.5, 2.8, 4.6, 1.5],
[5.7, 2.8, 4.5, 1.3],
[6.3, 3.3, 4.7, 1.6],
[4.9, 2.4, 3.3, 1. ],
[6.6, 2.9, 4.6, 1.3],
[5.2, 2.7, 3.9, 1.4],
[5. , 2. , 3.5, 1. ],
[5.9, 3. , 4.2, 1.5],
[6. , 2.2, 4. , 1. ],
[6.1, 2.9, 4.7, 1.4],
[5.6, 2.9, 3.6, 1.3],
[6.7, 3.1, 4.4, 1.4],
[5.6, 3. , 4.5, 1.5],
[5.8, 2.7, 4.1, 1. ],
[6.2, 2.2, 4.5, 1.5],
[5.6, 2.5, 3.9, 1.1],
[5.9, 3.2, 4.8, 1.8],
[6.1, 2.8, 4. , 1.3],
[6.3, 2.5, 4.9, 1.5],
[6.1, 2.8, 4.7, 1.2],
[6.4, 2.9, 4.3, 1.3],
[6.6, 3. , 4.4, 1.4],
[6.8, 2.8, 4.8, 1.4],
[6.7, 3. , 5. , 1.7],
[6. , 2.9, 4.5, 1.5],
[5.7, 2.6, 3.5, 1. ],
[5.5, 2.4, 3.8, 1.1],
[5.5, 2.4, 3.7, 1. ],
[5.8, 2.7, 3.9, 1.2],
[6. , 2.7, 5.1, 1.6],
[5.4, 3. , 4.5, 1.5],
[6. , 3.4, 4.5, 1.6],
[6.7, 3.1, 4.7, 1.5],
[6.3, 2.3, 4.4, 1.3],
[5.6, 3. , 4.1, 1.3],
[5.5, 2.5, 4. , 1.3],
[5.5, 2.6, 4.4, 1.2],
[6.1, 3. , 4.6, 1.4],
[5.8, 2.6, 4. , 1.2],
[5. , 2.3, 3.3, 1. ],
[5.6, 2.7, 4.2, 1.3],
[5.7, 3. , 4.2, 1.2],
[5.7, 2.9, 4.2, 1.3],
[6.2, 2.9, 4.3, 1.3],
[5.1, 2.5, 3. , 1.1],
[5.7, 2.8, 4.1, 1.3],
[6.3, 3.3, 6. , 2.5],
[5.8, 2.7, 5.1, 1.9],
[7.1, 3. , 5.9, 2.1],
[6.3, 2.9, 5.6, 1.8],
[6.5, 3. , 5.8, 2.2],
[7.6, 3. , 6.6, 2.1],
[4.9, 2.5, 4.5, 1.7],
[7.3, 2.9, 6.3, 1.8],
[6.7, 2.5, 5.8, 1.8],
[7.2, 3.6, 6.1, 2.5],
[6.5, 3.2, 5.1, 2. ],
[6.4, 2.7, 5.3, 1.9],
[6.8, 3. , 5.5, 2.1],
[5.7, 2.5, 5. , 2. ],
[5.8, 2.8, 5.1, 2.4],
[6.4, 3.2, 5.3, 2.3],
[6.5, 3. , 5.5, 1.8],
[7.7, 3.8, 6.7, 2.2],
[7.7, 2.6, 6.9, 2.3],
[6. , 2.2, 5. , 1.5],
[6.9, 3.2, 5.7, 2.3],
[5.6, 2.8, 4.9, 2. ],
[7.7, 2.8, 6.7, 2. ],
[6.3, 2.7, 4.9, 1.8],
[6.7, 3.3, 5.7, 2.1],
[7.2, 3.2, 6. , 1.8],
[6.2, 2.8, 4.8, 1.8],
[6.1, 3. , 4.9, 1.8],
[6.4, 2.8, 5.6, 2.1],
[7.2, 3. , 5.8, 1.6],
[7.4, 2.8, 6.1, 1.9],
[7.9, 3.8, 6.4, 2. ],
[6.4, 2.8, 5.6, 2.2],
[6.3, 2.8, 5.1, 1.5],
[6.1, 2.6, 5.6, 1.4],
[7.7, 3. , 6.1, 2.3],
[6.3, 3.4, 5.6, 2.4],
[6.4, 3.1, 5.5, 1.8],
[6. , 3. , 4.8, 1.8],
[6.9, 3.1, 5.4, 2.1],
[6.7, 3.1, 5.6, 2.4],
[6.9, 3.1, 5.1, 2.3],
[5.8, 2.7, 5.1, 1.9],
[6.8, 3.2, 5.9, 2.3],
[6.7, 3.3, 5.7, 2.5],
[6.7, 3. , 5.2, 2.3],
[6.3, 2.5, 5. , 1.9],
[6.5, 3. , 5.2, 2. ],
[6.2, 3.4, 5.4, 2.3],
[5.9, 3. , 5.1, 1.8]]),
\'target\': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]),
\'target_names\': array([\'setosa\', \'versicolor\', \'virginica\'], dtype=\'<U10\'),
\'DESCR\': \'Iris Plants Database\\n====================\\n\\nNotes\\n-----\\nData Set Characteristics:\\n :Number of Instances: 150 (50 in each of three classes)\\n :Number of Attributes: 4 numeric, predictive attributes and the class\\n :Attribute Information:\\n - sepal length in cm\\n - sepal width in cm\\n - petal length in cm\\n - petal width in cm\\n - class:\\n - Iris-Setosa\\n - Iris-Versicolour\\n - Iris-Virginica\\n :Summary Statistics:\\n\\n ============== ==== ==== ======= ===== ====================\\n Min Max Mean SD Class Correlation\\n ============== ==== ==== ======= ===== ====================\\n sepal length: 4.3 7.9 5.84 0.83 0.7826\\n sepal width: 2.0 4.4 3.05 0.43 -0.4194\\n petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)\\n petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)\\n ============== ==== ==== ======= ===== ====================\\n\\n :Missing Attribute Values: None\\n :Class Distribution: 33.3% for each of 3 classes.\\n :Creator: R.A. Fisher\\n :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)\\n :Date: July, 1988\\n\\nThis is a copy of UCI ML iris datasets.\\nhttp://archive.ics.uci.edu/ml/datasets/Iris\\n\\nThe famous Iris database, first used by Sir R.A Fisher\\n\\nThis is perhaps the best known database to be found in the\\npattern recognition literature. Fisher\\\'s paper is a classic in the field and\\nis referenced frequently to this day. (See Duda & Hart, for example.) The\\ndata set contains 3 classes of 50 instances each, where each class refers to a\\ntype of iris plant. One class is linearly separable from the other 2; the\\nlatter are NOT linearly separable from each other.\\n\\nReferences\\n----------\\n - Fisher,R.A. "The use of multiple measurements in taxonomic problems"\\n Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to\\n Mathematical Statistics" (John Wiley, NY, 1950).\\n - Duda,R.O., & Hart,P.E. (1973) Pattern Classification and Scene Analysis.\\n (Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.\\n - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System\\n Structure and Classification Rule for Recognition in Partially Exposed\\n Environments". IEEE Transactions on Pattern Analysis and Machine\\n Intelligence, Vol. PAMI-2, No. 1, 67-71.\\n - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions\\n on Information Theory, May 1972, 431-433.\\n - See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II\\n conceptual clustering system finds 3 classes in the data.\\n - Many, many more ...\\n\',
\'feature_names\': [\'sepal length (cm)\',
\'sepal width (cm)\',
\'petal length (cm)\',
\'petal width (cm)\']}
iris.data
结果:

array([[5.1, 3.5, 1.4, 0.2], [4.9, 3. , 1.4, 0.2], [4.7, 3.2, 1.3, 0.2], [4.6, 3.1, 1.5, 0.2], [5. , 3.6, 1.4, 0.2], [5.4, 3.9, 1.7, 0.4], [4.6, 3.4, 1.4, 0.3], [5. , 3.4, 1.5, 0.2], [4.4, 2.9, 1.4, 0.2], [4.9, 3.1, 1.5, 0.1], [5.4, 3.7, 1.5, 0.2], [4.8, 3.4, 1.6, 0.2], [4.8, 3. , 1.4, 0.1], [4.3, 3. , 1.1, 0.1], [5.8, 4. , 1.2, 0.2], [5.7, 4.4, 1.5, 0.4], [5.4, 3.9, 1.3, 0.4], [5.1, 3.5, 1.4, 0.3], [5.7, 3.8, 1.7, 0.3], [5.1, 3.8, 1.5, 0.3], [5.4, 3.4, 1.7, 0.2], [5.1, 3.7, 1.5, 0.4], [4.6, 3.6, 1. , 0.2], [5.1, 3.3, 1.7, 0.5], [4.8, 3.4, 1.9, 0.2], [5. , 3. , 1.6, 0.2], [5. , 3.4, 1.6, 0.4], [5.2, 3.5, 1.5, 0.2], [5.2, 3.4, 1.4, 0.2], [4.7, 3.2, 1.6, 0.2], [4.8, 3.1, 1.6, 0.2], [5.4, 3.4, 1.5, 0.4], [5.2, 4.1, 1.5, 0.1], [5.5, 4.2, 1.4, 0.2], [4.9, 3.1, 1.5, 0.1], [5. , 3.2, 1.2, 0.2], [5.5, 3.5, 1.3, 0.2], [4.9, 3.1, 1.5, 0.1], [4.4, 3. , 1.3, 0.2], [5.1, 3.4, 1.5, 0.2], [5. , 3.5, 1.3, 0.3], [4.5, 2.3, 1.3, 0.3], [4.4, 3.2, 1.3, 0.2], [5. , 3.5, 1.6, 0.6], [5.1, 3.8, 1.9, 0.4], [4.8, 3. , 1.4, 0.3], [5.1, 3.8, 1.6, 0.2], [4.6, 3.2, 1.4, 0.2], [5.3, 3.7, 1.5, 0.2], [5. , 3.3, 1.4, 0.2], [7. , 3.2, 4.7, 1.4], [6.4, 3.2, 4.5, 1.5], [6.9, 3.1, 4.9, 1.5], [5.5, 2.3, 4. , 1.3], [6.5, 2.8, 4.6, 1.5], [5.7, 2.8, 4.5, 1.3], [6.3, 3.3, 4.7, 1.6], [4.9, 2.4, 3.3, 1. ], [6.6, 2.9, 4.6, 1.3], [5.2, 2.7, 3.9, 1.4], [5. , 2. , 3.5, 1. ], [5.9, 3. , 4.2, 1.5], [6. , 2.2, 4. , 1. ], [6.1, 2.9, 4.7, 1.4], [5.6, 2.9, 3.6, 1.3], [6.7, 3.1, 4.4, 1.4], [5.6, 3. , 4.5, 1.5], [5.8, 2.7, 4.1, 1. ], [6.2, 2.2, 4.5, 1.5], [5.6, 2.5, 3.9, 1.1], [5.9, 3.2, 4.8, 1.8], [6.1, 2.8, 4. , 1.3], [6.3, 2.5, 4.9, 1.5], [6.1, 2.8, 4.7, 1.2], [6.4, 2.9, 4.3, 1.3], [6.6, 3. , 4.4, 1.4], [6.8, 2.8, 4.8, 1.4], [6.7, 3. , 5. , 1.7], [6. , 2.9, 4.5, 1.5], [5.7, 2.6, 3.5, 1. ], [5.5, 2.4, 3.8, 1.1], [5.5, 2.4, 3.7, 1. ], [5.8, 2.7, 3.9, 1.2], [6. , 2.7, 5.1, 1.6], [5.4, 3. , 4.5, 1.5], [6. , 3.4, 4.5, 1.6], [6.7, 3.1, 4.7, 1.5], [6.3, 2.3, 4.4, 1.3], [5.6, 3. , 4.1, 1.3], [5.5, 2.5, 4. , 1.3], [5.5, 2.6, 4.4, 1.2], [6.1, 3. , 4.6, 1.4], [5.8, 2.6, 4. , 1.2], [5. , 2.3, 3.3, 1. ], [5.6, 2.7, 4.2, 1.3], [5.7, 3. , 4.2, 1.2], [5.7, 2.9, 4.2, 1.3], [6.2, 2.9, 4.3, 1.3], [5.1, 2.5, 3. , 1.1], [5.7, 2.8, 4.1, 1.3], [6.3, 3.3, 6. , 2.5], [5.8, 2.7, 5.1, 1.9], [7.1, 3. , 5.9, 2.1], [6.3, 2.9, 5.6, 1.8], [6.5, 3. , 5.8, 2.2], [7.6, 3. , 6.6, 2.1], [4.9, 2.5, 4.5, 1.7], [7.3, 2.9, 6.3, 1.8], [6.7, 2.5, 5.8, 1.8], [7.2, 3.6, 6.1, 2.5], [6.5, 3.2, 5.1, 2. ], [6.4, 2.7, 5.3, 1.9], [6.8, 3. , 5.5, 2.1], [5.7, 2.5, 5. , 2. ], [5.8, 2.8, 5.1, 2.4], [6.4, 3.2, 5.3, 2.3], [6.5, 3. , 5.5, 1.8], [7.7, 3.8, 6.7, 2.2], [7.7, 2.6, 6.9, 2.3], [6. , 2.2, 5. , 1.5], [6.9, 3.2, 5.7, 2.3], [5.6, 2.8, 4.9, 2. ], [7.7, 2.8, 6.7, 2. ], [6.3, 2.7, 4.9, 1.8], [6.7, 3.3, 5.7, 2.1], [7.2, 3.2, 6. , 1.8], [6.2, 2.8, 4.8, 1.8], [6.1, 3. , 4.9, 1.8], [6.4, 2.8, 5.6, 2.1], [7.2, 3. , 5.8, 1.6], [7.4, 2.8, 6.1, 1.9], [7.9, 3.8, 6.4, 2. ], [6.4, 2.8, 5.6, 2.2], [6.3, 2.8, 5.1, 1.5], [6.1, 2.6, 5.6, 1.4], [7.7, 3. , 6.1, 2.3], [6.3, 3.4, 5.6, 2.4], [6.4, 3.1, 5.5, 1.8], [6. , 3. , 4.8, 1.8], [6.9, 3.1, 5.4, 2.1], [6.7, 3.1, 5.6, 2.4], [6.9, 3.1, 5.1, 2.3], [5.8, 2.7, 5.1, 1.9], [6.8, 3.2, 5.9, 2.3], [6.7, 3.3, 5.7, 2.5], [6.7, 3. , 5.2, 2.3], [6.3, 2.5, 5. , 1.9], [6.5, 3. , 5.2, 2. ], [6.2, 3.4, 5.4, 2.3], [5.9, 3. , 5.1, 1.8]])
iris.target
结果:

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
#切分数据集
Xtrain, Xtest, ytrain, ytest = train_test_split(iris.data,
iris.target,
random_state=42)#random_state:随机数种子,值为整数时,使每次划分结果都一样,可调
len(Xtrain)#112 len(Xtest)#38
ytrain
结果:

array([0, 0, 2, 1, 1, 0, 0, 1, 2, 2, 1, 2, 1, 2, 1, 0, 2, 1, 0, 0, 0, 1, 2, 0, 0, 0, 1, 0, 1, 2, 0, 1, 2, 0, 2, 2, 1, 1, 2, 1, 0, 1, 2, 0, 0, 1, 1, 0, 2, 0, 0, 1, 1, 2, 1, 2, 2, 1, 0, 0, 2, 2, 0, 0, 0, 1, 2, 0, 2, 2, 0, 1, 1, 2, 1, 2, 0, 2, 1, 2, 1, 1, 1, 0, 1, 1, 0, 1, 2, 2, 0, 1, 2, 2, 0, 2, 0, 1, 2, 2, 1, 2, 1, 1, 2, 2, 0, 1, 2, 0, 1, 2])
ytest
结果:

array([1, 0, 2, 1, 1, 0, 1, 2, 1, 1, 2, 0, 0, 0, 0, 1, 2, 1, 1, 2, 0, 2,
0, 2, 2, 2, 2, 2, 0, 0, 0, 0, 1, 0, 0, 2, 1, 0])
#建模 clf = GaussianNB()#初始化高斯分布朴素贝叶斯 clf.fit(Xtrain, ytrain)#带入训练集进行训练
结果:GaussianNB(priors=None)
#在测试集上执行预测 clf.predict(Xtest)
结果:array([1, 0, 2, 1, 1, 0, 1, 2, 1, 1, 2, 0, 0, 0, 0, 1, 2, 1, 1, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0, 0, 0, 1, 0, 0, 2, 1, 0])
clf.predict_proba(Xtest)#在测试集上执行预测,proba导出的是每个样本属于某类的概率
结果:

array([[5.97926853e-094, 9.95499546e-001, 4.50045384e-003], [1.00000000e+000, 1.52146968e-013, 1.07136902e-020], [1.71330808e-299, 6.04667826e-012, 1.00000000e+000], [2.88508207e-096, 9.76485329e-001, 2.35146713e-002], [1.36797133e-109, 8.51147229e-001, 1.48852771e-001], [1.00000000e+000, 4.74962788e-013, 4.28854236e-021], [3.25153316e-053, 9.99959350e-001, 4.06500520e-005], [1.09216160e-176, 1.05015117e-006, 9.99998950e-001], [3.27169186e-098, 9.93646597e-001, 6.35340277e-003], [1.17401351e-060, 9.99944993e-001, 5.50073382e-005], [1.00765817e-153, 5.02929583e-004, 9.99497070e-001], [1.00000000e+000, 7.95517827e-017, 5.80301835e-025], [1.00000000e+000, 1.83324108e-016, 2.96899989e-024], [1.00000000e+000, 1.81709952e-016, 2.19054140e-024], [1.00000000e+000, 2.58611124e-016, 6.24907433e-024], [4.90534771e-110, 5.45081346e-001, 4.54918654e-001], [3.16184825e-207, 5.32942939e-007, 9.99999467e-001], [5.54971964e-057, 9.99985948e-001, 1.40522914e-005], [2.35216801e-087, 9.98060492e-001, 1.93950811e-003], [8.52134069e-195, 3.31416502e-006, 9.99996686e-001], [1.00000000e+000, 2.01691401e-015, 2.19989447e-023], [1.10030136e-129, 9.28827573e-002, 9.07117243e-001], [1.00000000e+000, 3.55180650e-013, 3.14309037e-021], [4.61090739e-188, 1.99740486e-005, 9.99980026e-001], [5.38997715e-243, 9.37394931e-010, 9.99999999e-001], [8.41240591e-181, 1.33362177e-006, 9.99998666e-001], [7.84665916e-184, 7.04291221e-004, 9.99295709e-001], [4.06568213e-222, 1.32017082e-008, 9.99999987e-001], [1.00000000e+000, 7.64632371e-015, 2.10335817e-023], [1.00000000e+000, 4.36746748e-015, 3.82841755e-023], [1.00000000e+000, 1.67045858e-018, 1.11343221e-026], [1.00000000e+000, 6.19486746e-016, 6.98399326e-023], [1.29430190e-090, 9.62168850e-001, 3.78311504e-002], [1.00000000e+000, 6.72672239e-016, 1.17370919e-023], [1.00000000e+000, 5.25411235e-017, 2.85220284e-025], [4.98861144e-142, 3.13601455e-002, 9.68639854e-001], [2.84242806e-097, 9.05614884e-001, 9.43851163e-002], [1.00000000e+000, 2.90496807e-016, 5.87418518e-024]])
#测试准确率 accuracy_score(ytest, clf.predict(Xtest))#1.0
2. MultinomialNB
MultinomialNB就是先验为多项式分布的朴素贝叶斯。它假设特征是由一个简单多项式分布生成的。多项分布可以描述各种类型样本出现次数的概率,因此多项式朴素贝叶斯非常适合用于描述出现次数或者出现次数比例的特征。该模型常用于文本分类,特征表示的是次数,例如某个词语的出现次数。
多项式分布公式如下: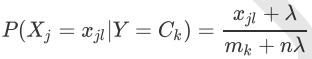
其中,P(Xj = xjl | Y = Ck)是第k个类别的第j维特征的第l个取值条件概率。mk是训练集中输出为第k类的样本个数。 λ 为一个大于0的常数,常常取为1,即拉普拉斯平滑。也可以取其他值。 分子分母都加 λ 的作用是防止概率为0的情况出现。
3. BernoulliNB
BernoulliNB就是先验为伯努利分布的朴素贝叶斯。假设特征的先验概率为二元伯努利分布,即如下式: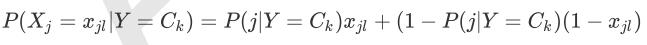
此时l 只有两种取值。 xjl只能取值0或者1。
在伯努利模型中,每个特征的取值是布尔型的,即true和false,或者1和0。在文本分类中,就是一个特征有没有在一个文档中出现。
总结:
- 一般来说,如果样本特征的分布大部分是连续值,使用GaussianNB会比较好。
- 如果如果样本特征的分布大部分是多元离散值,使用MultinomialNB比较合适。
- 而如果样本特征是二元离散值或者很稀疏的多元离散值,应该使用BernoulliNB。
三、朴素贝叶斯之鸢尾花数据实验
应用GaussianNB对鸢尾花数据集进行分类。
1. 导入数据集
import numpy as np import pandas as pd import random dataSet =pd.read_csv(\'iris.txt\',header = None) dataSet.head()
结果:
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | Iris-setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | Iris-setosa |
dataSet.shape#(150, 5)
2. 切分训练集和测试集
"""
函数功能:随机切分训练集和测试集
参数说明:
dataSet:输入的数据集
rate:训练集所占比例
返回:切分好的训练集和测试集
"""
def randSplit(dataSet, rate):
l = list(dataSet.index) #提取出索引
random.shuffle(l) #随机打乱索引
dataSet.index = l #将打乱后的索引重新赋值给原数据集
n = dataSet.shape[0] #总行数
m = int(n * rate) #训练集的数量
train = dataSet.loc[range(m), :] #提取前m个记录作为训练集
test = dataSet.loc[range(m, n), :] #剩下的作为测试集
dataSet.index = range(dataSet.shape[0]) #更新原数据集的索引
test.index = range(test.shape[0]) #更新测试集的索引
return train, test
l = list(dataSet.index) print(l)
结果:

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149]
random.shuffle(l) print(l) dataSet.index = l
结果:

[72, 43, 136, 132, 11, 102, 55, 103, 50, 85, 79, 53, 63, 5, 111, 16, 119, 113, 41, 133, 78, 19, 114, 104, 54, 4, 149, 106, 15, 57, 143, 126, 101, 128, 94, 66, 122, 0, 83, 146, 93, 84, 86, 3, 70, 76, 27, 14, 30, 20, 121, 39, 46, 10, 24, 109, 123, 56, 110, 77, 36, 125, 44, 22, 81, 140, 75, 144, 40, 91, 59, 130, 65, 64, 1, 117, 92, 37, 115, 118, 141, 29, 107, 105, 69, 87, 34, 80, 31, 61, 74, 25, 112, 9, 51, 148, 145, 142, 116, 6, 98, 60, 26, 67, 12, 131, 8, 129, 42, 7, 21, 82, 135, 96, 38, 99, 100, 62, 45, 89, 13, 47, 138, 68, 28, 108, 124, 73, 49, 52, 97, 48, 35, 17, 95, 32, 23, 33, 90, 134, 2, 137, 127, 147, 58, 71, 88, 139, 120, 18]
n = dataSet.shape[0] #总行数 m = int(n * 0.8) #训练集的数量
train = dataSet.loc[range(m), :]
train
结果:

0 1 2 3 4 0 4.6 3.6 1.0 0.2 Iris-setosa 1 6.9 3.1 5.1 2.3 Iris-virginica 2 5.0 2.3 3.3 1.0 Iris-versicolor 3 6.0 3.4 4.5 1.6 Iris-versicolor 4 5.7 2.9 4.2 1.3 Iris-versicolor 5 6.3 2.7 4.9 1.8 Iris-virginica 6 6.3 2.5 4.9 1.5 Iris-versicolor 7 6.4 2.7 5.3 1.9 Iris-virginica 8 5.1 2.5 3.0 1.1 Iris-versicolor 9 6.2 2.8 4.8 1.8 Iris-virginica 10 5.1 3.7 1.5 0.4 Iris-setosa 11 4.4 3.2 1.3 0.2 Iris-setosa 12 7.7 3.0 6.1 2.3 Iris-virginica 13 5.6 2.5 3.9 1.1 Iris-versicolor 14 5.0 3.3 1.4 0.2 Iris-setosa 15 4.4以上是关于机器学习_贝叶斯算法的主要内容,如果未能解决你的问题,请参考以下文章
