算法分析主要研究两个内容:时间复杂度 和 空间复杂度。
时间复杂度分析
一般来说,最关注的是时间复杂度。(或称时间上的增长数量级)
-
时间复杂度的渐进表示
-
渐近上界:
T(N)=O(f(N))表示 T(N) 的阶数小于或等于 f(N) 的阶数,这种记法称为大 O 标记法。(该算法不会比 f(N) 还坏)
写成极限形式就是: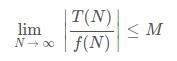 ,M为某一正常数
,M为某一正常数 -
渐近下界:
T(N)=Ω(g(N))表示 T(N) 的阶数大于或等于 g(N) 的阶数。(下界,该算法不可能比 g(N) 更好) -
渐近精确界:
T(N)=Θ(h(N))表示 T(N) 与 h(N) 的同阶。
极限形式: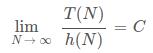 , C为某一非0常数
, C为某一非0常数 -
非渐近紧确上界:
T(N)=o(p(N))表示 T(N) 的阶数小于 p(N) 的阶数,称为小 o 标记法,他不同于大 O,因为大 O 包含增长率相同的情况。
T(N)=O(p(N))且T(N)≠Θ(p(N))则T(n)=o(p(N)). -
T(N) ~ q(N), 表示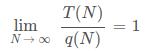 ,这比 Θ 更精确。(算法 4th 中主要就用这个)
,这比 Θ 更精确。(算法 4th 中主要就用这个)
-
-
时间复杂度的理论分析的一般过程
- 确定输入模型,定义问题的规模。(自变量M、N)
- 识别内循环
- 根据内循环中的操作定义成本模型。(访问数组的次数、修改数组内容等)
- 对于给定的输入,判断成本:即内循环操作执行的频率。这里可能需要做数学分析。(最常用的是累加操作和级数)
- 做倍率实验来验证结果。
-
注意事项
上述一般过程,在某些情况下可能会不适用- 大常数:一般的算法分析都会忽略其中的常数。但是如果常数接近问题的规模N时,这种近似就是错误的。
- 内循环是决定性因素的假设并不总是正确的。
- 对输入的强烈依赖:上述过程成立的前提之一是——运行时间和输入相对无关。若这个条件无法满足,可能会出现非预期的结果。
- 其他
空间损耗分析
对空间损耗的分析相对而言就简单很多,主要原因是它只涉及到会分配内存的语句。
不过话虽如此,对一个自带GC的、使用了各种 内存/性能 优化技术的代码,内存的使用可能会是一个复杂的动态过程,导致分析困难。
画外:各语言对空间损耗的态度
在 C/C++ 里可能会很在意空间,甚至为了节省内存,使出各种奇技淫巧。
但是在 Java 中,内存损耗向其他方面作出了妥协:
- 删除了无符号整数,规避了由它带来的坑。
- 数组自带长度信息,索引越界变得很容易检测。
- 真正的数组(等同于 C 的数组)存放在堆中,然后用一个 Java数组对象包装它,这个对象包含 16 bytes 的对象开销、4 bytes 保存长度信息和 4 bytes 的填充字节。(一般内存的使用会以 8 bytes (对 64 位机) 为基本单位,缺的地方就填充)
- 自动内存管理GC,解放了程序员,提高了代码健壮性。代价是响应速度降低,(GC 可能会导致卡顿)内存和CPU使用提高。
而 Python3,就更进一步,连内存溢出也避免了,实现了“无限精度”运算。。算是用速度和内存为代价,提升了代码的表达能力、可读性,降低了学习难度,也规避了很多坑。
要再说到函数式语言如 Elixir,它们内部的所有量都是 Immutable,也就是不可变的类型。对它们的任何操作都会产生一个“副本”。(这和 C 语言感觉就像两个极端)在牺牲了内存的同时,在并发编程上得到了其他语言无法比拟的优势。
数据结构方面也有这样的例子,如 Hash Table,在提供更多内存的前提下,实现了几乎为常数的对象访问。
总结一下就是,越往底层的东西,就越在意节省内存。而在上层,内存往往会让步给代码可读性、健壮性、并发性、访问速度等等。
而在大数据时代下,并发性、访问速度、健壮性、灾容设计等变得越来越重要。仅为了灾容,一份数据就往往会在不同的地方有好几个副本。甚至已经出现了完全运行在内存条里的高速数据库。
空间一直在给这些指标不断让步。不过得益于内存价格的不断降低,这个让步大概还能持续很久。