遗传算法求解最优值

Posted 2020-11-04 Aaron12

1、遗传算法介绍

遗传算法，模拟进化论的自然选择和生物进化构成的计算模型，一种不断选择优良个体的算法。谈到遗传，想想自然界动物遗传是怎么来的，自然主要过程包括染色体的选择，交叉，变异，这些操作后，保证了以后的个基本上是最优的，那么以后再继续迭代这样下去，就可以一直最优了。

2、解决的问题

遗传算法能解决的问题很多了，但是遗传算法主要还是解决优化类问题，尤其是那种不能直接解出来的很复杂的问题，而实际情况通常也是这样的。

本部分主要为了了解遗传算法的应用，选择一个复杂的二维函数来进行遗传算法优化，函数显示为y=10*sin(5*x)+7*abs(x-5)+10,这个函数图像为：

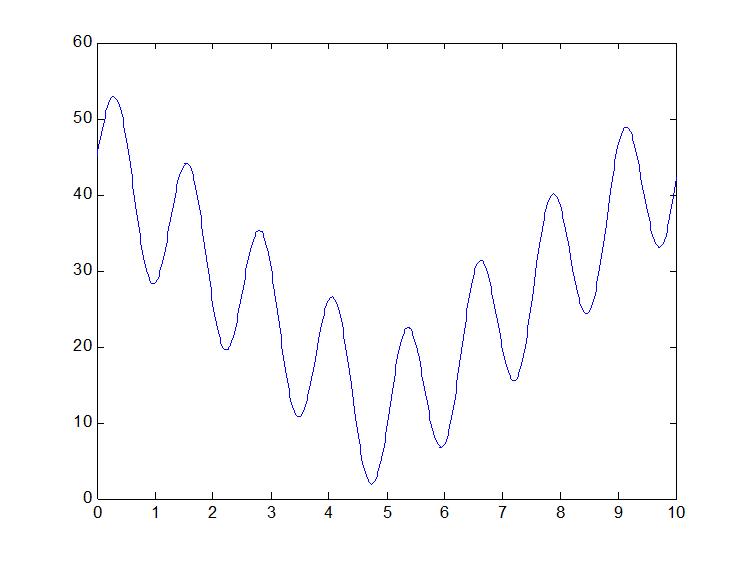
当然函数你还可以任意假设和编写，只要符合就可以。要求它的最大值（这个貌似可以，很容易写出来----如果再复杂一点估计就不行了）       这类问题如果用遗传算法或者其他优化方法就很简单，举个例子吧，我把x等分成100万份，再一下子都带值进去算，求出对应的100万个y的值，再比较他们的大小找到最大值不就可以了吗，很笨吧，人算是不可能的，但是计算机可以。遗传算法也是很笨的一个个搜索，只不过家里一点什么了，就是人为的给它算的方向和策略，让它有目的的算，这也就是算法了。

3、如何开始？

首先是选择个体了。遗传算法中有多个个体，这样相互结合的机会才多，产生的后代才会多种多样，才会有更好的优良基因，有利于种群的发展。那么算法也是如此，当然个体多少是个问题，一般来说20-100之间我觉得差不多了。那么个体究竟是什么呢？在我们这个问题中自然就是x值了。其他情况下，个体就是所求问题的变量，这里我们假设个体数选100个，也就是开始选100个不同的x值，不明白的话就假设是100个猴子吧。好了，现在有了100个猴子组成的一个种群，那么这个种群应该怎么发展才能越来越好？说到这，我们想想，如何定义这个越来越好呢？这个应该有一个评价指标吧。在我们的这个问题中，好像是对应的y值越大越好是吧。我们甚至可以给他们拍个名来决定哪些好哪些不好。我们把这个叫做对于个体的适应度，这应该算是算法的后半部分才对。

4、编码

首先明白什么是编码？为什么要编码？如何编码？

好，什么是编码？其实编码就是把自变量（x）换一下形式而已，转换为计算机能够识别的方式，在这个形式下，更容易操作其他过程（比如交叉，变异什么的）而已。一般的编码都是二进制编码，自然数编码，矩阵编码等等，二用的最多的可以说是二进制编码，感觉这和人体DNA，基因的排列很相似。想想DNA怎么排的？不就是在两条长链上一对一排的吗？那么什么是二进制编码？很简单，就是1,0,1,0对应的来回组合排列而已。比如：1100100010, 0011001001等等，这些都是位数长度为10的二进制编码。那么就又来一个问题，怎样去扩大这个精度呢？如果要保持0-5不变的话，只能增加位数了，把9位编码编程10位，20位，100位，哇，够大了吧，变成100个0,1组合，很恐怖吧，事实上，究竟是多少要视情况而定，一般20位左右感觉就可以了，虽然说越大越好，但是太大了消耗内存，速度慢了，不值。

5、关于交叉与变异

基因发生突变就叫变异，有了编码的概念，那就在编码基础上来说变异（某一位编码变了）。最简单的变异是单个点的变异。现在以10位长的编码来说，比如把x=3编码一下，随便假设为11000 10010吧，好了，在变异操作时，假设第5位变异了（0变1· 1变0），那么这个时候变成什么了？那肯定不是3了，是多少是肯定可以反算回去的，这里懒得算了，就假设为3.213吧，发没发现，这样一来，x是不是变了？既然变了就好啊，带到原函数（适应度函数）里面比较这两个x值对应的哪个y值大一写，如果后面变异后的大一些是不是就是说产生了好的变异啊，就可以在下一次个体选择的时候选择它了。那么想想很多x来一起变异会怎么样呢？肯定会生成很多很多的解吧，反复这么做会怎么样呢？只要每次都保留最优解的话，我来个循环100万次，也总能找到解吧，当然这么多次得花多久，也不太合适，这还只是一个点位在进行变异，若果每次我让多个点位变异呢？哇，又不可思议了，变化更大了吧。当然，变异不止如此，更多的去看专业的论文吧。知道了变异是干什么的，剩下的都好说了，好了，这还是变异，想想自然界遗传中除了变异还有什么？交叉吧，那么交叉又是什么？

学过生物的都知道，动物交配时，部分染色体干什么了？是不是交叉了？就是把相应部分的基因交换了。再以编码为例（某一段编码变了 互相交换），比如现在随便从100个x值中选取两个吧，鸡舍正好选中了x=3和4，对应的编码假设是11001 10101 和00101 01011，那么怎么交叉呢？我们知道每次交叉的染色体通常是一块一块的，恩，这里在算法设计上也来一块一块的吧。比如说就把位置在2,3,4号的编码给整体交叉了，那么x=3对应的位置是100吧，x=4对应的位置是010吧，好，交换以后x=3对应的位置就变成了010，x=4对应的位置就变成100，加回去就变成什么了？x=3是不是就是10101 10101，x=4是不是就是01001 01011了。而现在，把他们再反编码回去还是x=3和x=4吗？显然又不是了吧（当然也有小概率是一样的吧，很小）。那是什么？不想算，还是假设吧，假设为3.234和4.358吧，好了新的个体是不是又来了？恩，同理，带到适应度函数里面去吧，再取优秀个体，完事。同样，有些专门研究这种算法的开发出来各种各样的交叉方式，什么一个个体的钱3个与后一个个体的后三个交叉，中间几位来交叉等等，总之就是生产新个体。而这样做的目的在哪呢？无非是三个字，随机性，充分保证生产新个体具有随机性，你说你的x=3变异后为3.2,3.2什么的距离3那么近，在一些存在局部最优解的问题上就永远跳不出局部最优解，相反，你的x=1一下子变异成了x=5，哇，好大的变化，一下从这头到了那头，这对于算法的广阔搜索能力来说是非常好的。

6、关于选择的问题

选择最符合条件的个体，对应到本问题来说，每次交叉或者变异是不是产生了新的个体？如果这些个体都保留下来的话，种群是要爆炸的，而且在算法里面，我们还规定的是每次循环都必须保证都是100个个体。那么必须在200个个体中剔除100个吧，如何剔除呢？有人说很简单，排名吧，取前100号x不就可以了吗？排名这个东西真的好吗？我就不信，凭什么差一点的不能选上，搞不好在下一次变异中一下子冲到了第一呢？这个问题在选择上也有一些对应的规则，最通用的就是轮盘赌法，简单来说就是一种概率选择法（当然还有许多其他的方法，感兴趣的自己搜相关的文献吧，我也没用过）。什么是轮盘赌法呢？就是把对应所有y值（适应度函数值）加起来，在用各自的y值去除以这个sum值，这样是不是谁的概率大谁的概率小就很清楚了？然后再随机生成一个0-1的概率值p，谁在p的范围里面是不是就选择谁，比如说x=3时在100个x中y的值最大，那么选择它的概率是不是就最大，比如说是0.1（0.1小吗？不小了好吧，想想其他的会是什么，都比0.1小，那么从概率上讲，选100次的话，是不是就有10次宣导x=3，其他的都不足10次是吧，那么在下一次100个种群个体中就有10个x=3了，再来一回可能就有20个x=3的个体了。再就是30个，最后就只剩下100个x=3的个体了，它自己在哪里交叉变异已经没有意义了，如果到了这个时候就意味着这个算法可以结束了）。再详细点，如下图所示吧：现在要在下面三个大类中选取100个x个体，轮盘赌转100次以后，是不是个艺术落在s3中的个体多一些，选择的原理就是这样，再不明白直接后面的程序吧。

 

7、还差点什么呢

至此，感觉也差不多了吧，选择完后在重复上述步骤交叉，变异等等，那么什么时候是个头了？很简单，办法就是迭代次数，迭代10次看一下结果，20次，看一下结果，30次，40次，100次，当次数达到一定程度以后，优秀的个体越来越多，大都集中在最优解附近，即使变异或者交叉了也是在这个最优解附近，没有影响的。在下一次选择就又变回来了，那么至此就真的结束了。比如说先来结果吧，该问题按我的思路做完后，迭代100次变成什么样子了？看图：

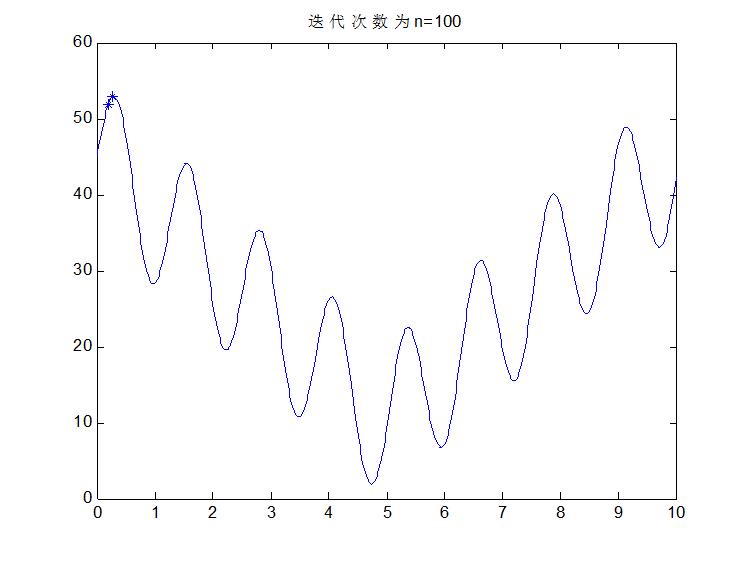
代码如下

主函数：

function main()
clear;
clc;
%种群大小
popsize=100;
%二进制编码长度
chromlength=10;
%交叉概率
pc = 0.6;
%变异概率
pm = 0.001;
%初始种群
pop = initpop(popsize,chromlength);

for i = 1:100
    %计算适应度值（目标函数值）
    objvalue = cal_objvalue(pop);
    fitvalue = objvalue;
    %选择操作
    newpop = selection(pop,fitvalue);
    %交叉操作
    newpop = crossover(newpop,pc);
    %变异操作
    newpop = mutation(newpop,pm);
    %更新种群
    pop = newpop;
    %寻找最优解
    [bestindividual,bestfit] = best(pop,fitvalue);
    x2 = binary2decimal(bestindividual);
    x1 = binary2decimal(newpop);
    y1 = cal_objvalue(newpop);
    if mod(i,10) == 0
        figure;
        fplot(\'10*sin(5*x)+7*abs(x-5)+10\',[0 10]);
        hold on;
        plot(x1,y1,\'*\');
        title([\'迭代次数为n=\' num2str(i)]);
        %plot(x1,y1,\'*\');
    end
end
fprintf(\'The best X is --->>%5.2f\\n\',x2);
fprintf(\'The best Y is --->>%5.2f\\n\',bestfit);

初始化种群：

%初始化种群大小
%输入变量：
%popsize：种群大小
%chromlength：染色体长度-->>转化的二进制长度
%输出变量：
%pop：种群
function pop=initpop(popsize,chromlength)
pop = round(rand(popsize,chromlength));
%rand(3,4)生成3行4列的0-1之间的随机数
% rand(3,4)
% 
% ans =
% 
%     0.8147    0.9134    0.2785    0.9649
%     0.9058    0.6324    0.5469    0.1576
%     0.1270    0.0975    0.9575    0.9706
%round就是四舍五入
% round(rand(3,4))=
% 1 1 0 1
% 1 1 1 0
% 0 0 1 1
%所以返回的种群就是每行是一个个体，列数是染色体长度

计算适应度值（目标函数值）：

%计算函数目标值
%输入变量：二进制数值
%输出变量：目标函数值
function [objvalue] = cal_objvalue(pop)
x = binary2decimal(pop);
%转化二进制数为x变量的变化域范围的数值
objvalue=10*sin(5*x)+7*abs(x-5)+10;

选择：

%如何选择新的个体
%输入变量：pop二进制种群，fitvalue：适应度值
%输出变量：newpop选择以后的二进制种群
function [newpop] = selection(pop,fitvalue)
%构造轮盘
[px,py] = size(pop);
totalfit = sum(fitvalue);
p_fitvalue = fitvalue/totalfit;
p_fitvalue = cumsum(p_fitvalue);%概率求和排序
ms = sort(rand(px,1));%从小到大排列
fitin = 1;
newin = 1;
while newin<=px
    if(ms(newin))<p_fitvalue(fitin)
        newpop(newin,:)=pop(fitin,:);
        newin = newin+1;
    else
        fitin=fitin+1;
    end
end

交叉：

%交叉变换
%输入变量：pop：二进制的父代种群数，pc：交叉的概率
%输出变量：newpop：交叉后的种群数
function [newpop] = crossover(pop,pc)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:2:px-1
    if(rand<pc)
        cpoint = round(rand*py);
        newpop(i,:) = [pop(i,1:cpoint),pop(i+1,cpoint+1:py)];
        newpop(i+1,:) = [pop(i+1,1:cpoint),pop(i,cpoint+1:py)];
    else
        newpop(i,:) = pop(i,:);
        newpop(i+1,:) = pop(i+1,:);
    end
end

变异：

%关于编译
%函数说明
%输入变量：pop：二进制种群，pm：变异概率
%输出变量：newpop变异以后的种群
function [newpop] = mutation(pop,pm)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
    if(rand<pm)
        mpoint = round(rand*py);
        if mpoint <= 0;
            mpoint = 1;
        end
        newpop(i,:) = pop(i,:);
        if newpop(i,mpoint) == 0
            newpop(i,mpoint) = 1;
        else newpop(i,mpoint) == 1
            newpop(i,mpoint) = 0;
        end
    else newpop(i,:) = pop(i,:);
    end
end

寻找最优解：

%求最优适应度函数
%输入变量：pop:种群，fitvalue:种群适应度
%输出变量：bestindividual:最佳个体，bestfit:最佳适应度值
function [bestindividual bestfit] = best(pop,fitvalue)
[px,py] = size(pop);
bestindividual = pop(1,:);
bestfit = fitvalue(1);
for i = 2:px
    if fitvalue(i)>bestfit
        bestindividual = pop(i,:);
        bestfit = fitvalue(i);
    end
end

解码：

%二进制转化成十进制函数
%输入变量：
%二进制种群
%输出变量
%十进制数值
function pop2 = binary2decimal(pop)
[px,py]=size(pop);
for i = 1:py
    pop1(:,i) = 2.^(py-i).*pop(:,i);
end
%sum(.,2)对行求和，得到列向量
temp = sum(pop1,2);
pop2 = temp*10/1023;