快速傅里叶变换 FFT

Posted 2020-11-04 fang-hao

难受难受难受！！！

好难啊！！！！

3月9日 凌晨

基本没有什么进展，只是照着大神的博客拍了一份板子，还是递归版的，好多语法问题么有弄明白，甚至没有搞清楚变换的前后的a为什么不一样2333333

实在太困了，明天继续，干巴爹！！o(*￣▽￣*)ブ

大神博客：[传送门](https://zhuanlan.zhihu.com/p/31584464)

 

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<algorithm>
 4 #include<cstring>
 5 #include<math.h>
 6 using namespace std;
 7 struct complex{
 8     double r,i;   //shi xu bu
 9     complex ( ) { }
10     complex (double r,double i):r(r),i(i) { }
11     inline void real (const double& x) {r=x;}
12     inline double real () {return r;}
13     inline complex operator + (const complex& temp)const{return complex(r+temp.r,i+temp.i);}
14     inline complex operator - (const complex& temp)const{return complex(r-temp.r,i-temp.i);}
15     inline complex operator * (const complex& temp)const{return complex(r*temp.r-i*temp.i,r*temp.i+i*temp.r);}
16     inline void operator /= (const double& x){r/=x,i/=x;}
17     inline void operator *= (const complex& temp){*this=complex(r*temp.r-i*temp.i,r*temp.i+i*temp.r);}
18     inline void operator += (const complex& temp){r+=temp.r,i+=temp.i;}
19     inline complex conj( ){return complex(r,-i);}
20 };
21 bool inverse=false;
22 const double PI=acos(-1.0);
23 const int N=10005;
24 complex a[50000];
25 inline complex W(const int& n,const int& k){
26     if(!inverse)return complex(cos(2*PI/n*k),sin(2*PI/n*k));
27     return complex(cos(2*PI/n*k),sin(2*PI/n*k)).conj();
28 }
29 inline void fft(complex *a,const int& n){
30     if(n==1)return;  // di gui zhong dian 
31     static complex buf[N];
32     const int m=n>>1;
33     for(register int i=0;i<m;i++){
34         buf[i]=a[i<<1];
35         buf[i+m]=a[i<<1|1]; 
36         //cout<<(i<<1)<<‘ ‘<<(i<<1|1)<<endl; 
37     }
38     memcpy(a,buf,sizeof(int)*(n+1));
39     complex *a1=a,*a2=a+m;
40     fft(a1,m);
41     fft(a2,m);
42     for(register int i=0;i<m;i++){
43         complex w=W(n,i);
44         buf[i]=a1[i]+w*a2[i];
45         buf[i+m]=a1[i]-w*a2[i];
46     }
47     memcpy(a,buf,sizeof(int)*(n+1));
48 }
49 int main(){
50     for(register int i=0;i<8;i++){
51         cin>>a[i].r;
52     }
53     fft(a,8);
54     for(register int i=0;i<8;i++){
55         cout<<a[i].r<<‘ ‘<<a[i].i<<endl;
56     }
57     inverse=true;
58     fft(a,8);
59     cout<<endl;
60     for(register int i=0;i<8;i++){
61         cout<<a[i].r<<‘ ‘<<a[i].i<<endl;
62     }

别点，辣眼睛！

 

ps：我恨指针！！！

这个整个写的是瓷（错）的。。。。。

 

FFT思路

首先假如我们有两个多项式，那么我们要求两个多项式的积，那么此时显然我们可以每一项都进行相乘，那么此时的复杂度是n^2,但是我们可以想到，这两个多项式如果用点集把他们表达出来，然后把点集相乘，这样就可以在n的复杂度内求出来，但是主要的问题是，如何把这两个多项式变成点值表达的形式，这时候就需要使用复数，因为复数有很多特殊性质。

整个过程应该是这样的：

1.在nlogn的时间内，把系数表达式变成点值表达式。
2.在n的时间内，把结果处理出来
3.在nlogn的时间内，把点值表达式变成系数表达式

 

具体过程分析

（部份内容引用自ljhandlwt的CSDN博客）

例如：n=4

y=a0+a1*x+a2*x^2+a3*x^3

求出x^4=1的4个根作为x坐标，求出相应的y坐标

1.按照x的指数的奇偶性，把y分成两部分，ya和yb

ya=a0+a2*x^2

yb=a1*x+a3*x^3=x(a1+a3*x^2)

2.定义y1，y2

y1=a0+a2*x

y2=a1+a3*x

3.得到了子问题之后，我们已知了y1和y2两个1次函数，那么我们要求出x^2=1的两个根作为x坐标，对应的y1和y2，这样就起到了分治的作用。

y(x)=y1(x^2)+x*y2(x^2);

4.将w[0,4]带入x，得到
y(w[0,4])=y1(w[0,4]^2)+w[0,4]*y2(w[0,4]^2)

根据公式1,w[0,4]^2=w[0,2],所以:
y(w[0,4])=y1(w[0,2])+w[0,4]*y2(w[0,2])

 

代入w[1,4],得到:
y(w[1,4])=y1(w[1,2])+w[1,4]*y2(w[1,2])

代入w[2,4],得到:
y(w[2,4])=y1(w[2,2])+w[2,4]*y2(w[2,2])

因为w[0,2]=w[2,2]，所以
y(w[2,4])=y1(w[0,2])+w[2,4]*y2(w[0,2])

代入w[3,4],得到:

y(w[3,4])=y1(w[1,2])+w[3,4]*y2(w[1,2])

写在一起就是:
y(w[0,4])=y1(w[0,2])+w[0,4]*y2(w[0,2])
y(w[1,4])=y1(w[1,2])+w[1,4]*y2(w[1,2])
y(w[2,4])=y1(w[2,2])+w[2,4]*y2(w[2,2])
y(w[3,4])=y1(w[1,2])+w[3,4]*y2(w[1,2])

因此，都可以由子问题的答案来处理。

复杂度：

f(n)=2*f(n/2)+O(n)

 

优化

因为在递归的算法中，不仅需要开一个临时数组进行记录，还因为进行了递归调用，常数巨大。

所以就引入了蝴蝶变换：

 

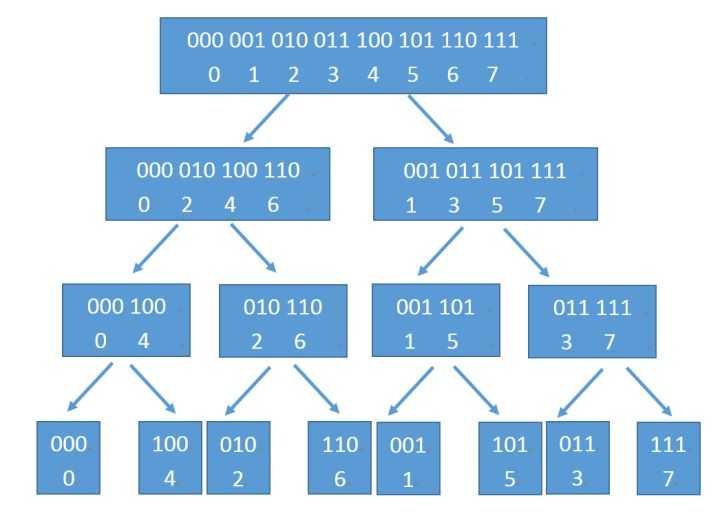
（图片引用自https://zhuanlan.zhihu.com/p/31584464)

 

观察每个数的二进制位，发现最后的每个位置的数的二进制位是原来数的二进制位的颠倒的顺序，所以我们可以先预处理出所有的位置的颠倒的二进制位的数，然后从倒数第二层向第一层计算，这样，我们不需要递归和临时存储了。

 

 

 P1919 【模板】A*B Problem升级版

代码

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<algorithm>
 4 #include<cstring>
 5 #include<math.h>
 6 using namespace std;
 7 struct cp{
 8     double r,i;
 9     cp(double tr=0.0,double ti=0.0){r=tr,i=ti;}
10     cp operator + (const cp a)const {return cp(r+a.r,i+a.i);}
11     cp operator - (const cp a)const {return cp(r-a.r,i-a.i);}
12     cp operator * (const cp a)const {return cp(r*a.r-i*a.i,r*a.i+i*a.r);}
13 };
14 cp a[500000],b[500000];
15 int ans[500000];
16 string s1,s2;
17 const double PI=acos(-1.0);
18 void fft(cp *a,int n,int INV){
19     for(register int i=0,j=0;i<n;i++){
20         if(i>j)swap(a[i],a[j]);
21         for(int l=n>>1;(j^=l)<l;l>>=1);
22     } 
23     for(register int l=2;l<=n;l<<=1){  // 倒数层数||长度
24         int m=l>>1;
25         cp Wtemp=cp(cos(2*PI*INV/l),sin(2*PI*INV/l));
26         for(register int i=0;i<n;i+=l){    //枚举每一段
27             cp W=cp(1,0);
28             for(register int j=0;j<m;j++){      //枚举每一段中的每一个
29                 cp temp=W*a[m+i+j];
30                 a[m+i+j]=a[i+j]-temp;
31                 a[i+j]=a[i+j]+temp;
32                 W=W*Wtemp;
33             }
34         }
35     }
36     if(INV==-1){
37         for(register int i=0;i<n;i++)a[i].r/=n;
38     }
39 }
40 int main(){
41     int n;
42     cin>>n;
43     cin>>s1>>s2;
44     for(register int i=0;i<n;i++){
45         a[i].r=s1[n-1-i]-‘0‘;
46         b[i].r=s2[n-1-i]-‘0‘;
47     }
48     int len=(1<<(int)(log2(n)+2));
49     fft(a,len,1);   fft(b,len,1);
50     for(register int i=0;i<len;i++) a[i]=a[i]*b[i];
51     fft(a,len,-1);
52     for(register int i=0;i<len;i++)ans[i]=floor(a[i].r+0.5);
53     int to=len;
54     while(ans[to]==0)  {to--;}
55     if(ans[to]>=10)to++;
56     for(register int i=0;i<to;i++)
57         if(ans[i]>=10)
58             ans[i+1]=ans[i+1]+ans[i]/10,ans[i]=ans[i]%10;
59     for(register int i=to;i>=0;i--)cout<<ans[i];
60     cout<<endl;
61 }

 

注意事项

在进行fft的时候，一定要注意，每次进行fft的len应该是一样的，不然会出现很多蜜汁bug，另外，下标从0开始，从个位向高位进行存储，这样更容易去前导零。

还有，两个n位数相乘，最多会得到2*n长度的数。

 

 

 

P3803 【模板】多项式乘法（FFT）

代码

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<algorithm>
 4 #include<cstring>
 5 #include<math.h>
 6 using namespace std;
 7 struct cp{
 8     double r,i;
 9     cp(double tr=0.0,double ti=0.0){r=tr,i=ti;}
10     cp operator + (const cp a)const {return cp(a.r+r,a.i+i);}
11     cp operator - (const cp a)const {return cp(r-a.r,i-a.i);}
12     cp operator * (const cp a)const {return cp(a.r*r-a.i*i,a.r*i+a.i*r);}
13 };
14 cp a[9000005],b[9000005];
15 const double PI=acos(-1.0);
16 void fft(cp *a,int n,int INV){
17     for(register int i=0,j=0;i<n;i++){
18         if(i>j)swap(a[i],a[j]);
19         for(register int l=n>>1;(j^=l)<l;l>>=1);
20     }
21     for(register int l=2;l<=n;l<<=1){
22         int m=l>>1;
23         cp Wtemp=cp(cos(2*PI*INV/l),sin(2*PI*INV/l));
24         for(register int i=0;i<n;i+=l){
25             cp W=cp(1,0);
26             for(register int j=0;j<m;j++){
27                 cp temp=W*a[m+i+j];
28                 a[m+i+j]=a[i+j]-temp;
29                 a[i+j]=a[i+j]+temp;
30                 W=W*Wtemp;
31             }
32         }
33     }
34     if(INV==-1)for(register int i=0;i<n;i++)a[i].r/=n;
35 }
36 int main(){
37     std::ios::sync_with_stdio(false);
38     int n,m;
39     cin>>n>>m;
40     int l=n+m+2;
41     int len=(1<<(int)(log2(l)+1));
42     //cout<<len<<endl;
43     for(register int i=n;i>=0;i--){
44         cin>>a[i].r;
45     }
46     for(register int i=m;i>=0;i--){
47         cin>>b[i].r;
48     }
49     fft(a,len,1); fft(b,len,1);
50     for(register int i=len;i>=0;i--){
51         a[i]=a[i]*b[i];
52     }
53     fft(a,len,-1);
54     int to=len;
55     while(floor(a[to].r+0.5)==0){to--;}
56     for(register int i=to;i>=0;i--){
57         cout<<(long long)floor(a[i].r+0.5)<<‘ ‘;
58     }
59     cout<<endl;
60 }

 

注意：使用long long！！！！

还有，去前导零的时候朴素一点，不要骚操作qwq

 

暂时就到这里了

感谢： 邓祎明的知乎教程
https://zhuanlan.zhihu.com/p/31584464

以及：ljhandlwt的CSDN教程

http://blog.csdn.net/ljhandlwt/article/details/51999762