归并排序

Posted 2020-11-04 思而不学

一、归并排序

• 核心：有序子列的归并

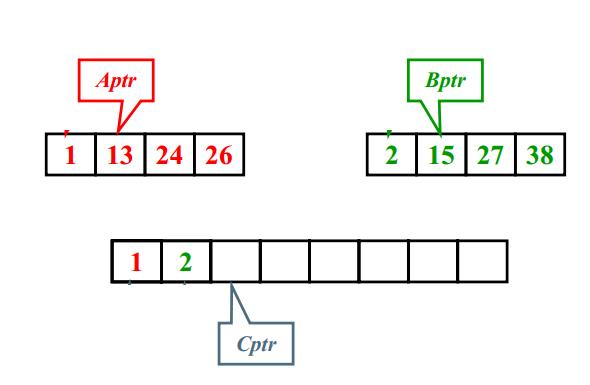
如果两个子列一共有N个元素，则归并的时间复杂度是？

T(N) = O(N)

/* L = 左边起始位置， R = 右边起始位置， RightEnd = 右边终点位置 */
void Merge(ElementType A[], ElementType TmpA[],
    int L, int R, int RightEnd)
{
    LeftEnd = R - 1;    /* 左边终点位置。假设左右两列挨着 */
    Tmp = L;            /* 存放结果的数组的初始位置 */
    NumElements = RightEnd - L + 1;
    while(L <= LeftEnd && R <= RightEnd) {
        if(A[L] <= A[R]) TmpA[Tmp++] = A[L++];
        else             TmpA[Tmp++] = A[R++];
    }
    while(L <= LeftEnd)     /* 直接复制左边剩下的 */
        TmpA[Tmp++] = A[L++];
    while(R <= RightEnd)    /* 直接复制右边剩下的 */
        TmpA[Tmp++] = A[R++];
    for(i=0; i<NumElements; i++, RightEnd--)
        A[RightEnd] = TmpA[RightEnd];
}

 

二、递归算法

• 分而治之

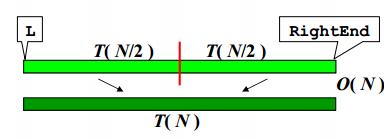
T(N)=T(N/2)+T(N/2)+O(N)

T(N)=O(NlogN)

 

• 统一函数接口

void Merge_Sort(ElementType A[], int N)
{
    ElementType *TmpA;
    TmpA = malloc(N*sizeof(ElementType));
    if(TmpA != NULL) {
        MSort(A, TmpA, 0, N-1);
        free(TmpA);
    } else 
        Error("Space not enough");
}

• 如果只在Merge中声明临时数组
  • void Merge(ElementType A[], int L, int R, int RightEnd)
  • void MSort(ElementType A[], int L, int RightEnd)

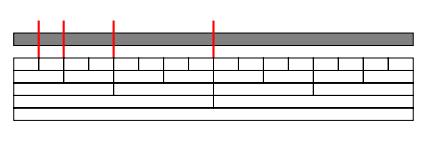
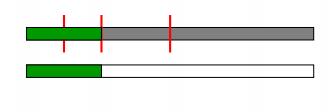
三、非递归算法

void Merge_Pass(ElementType A[], ElementType TmpA[], int N,
    int length)     /* length = 当前有序子列的长度 */
{
    for(i=0;i<=N-2*lenght;i+=2*lenght)
        Merge1(A, TmpA, i, i+length, i+2*length-1);
    if(i+length < N)    /* 归并最后2个子列 */
        Merge1(A, TmpA, i, i+length, N-1);
    else                /* 最后只剩1个子列 */
        for(j=i;j<N;j++)    TmpA[j] = A[j];
}

 

void Merge_Sort(ElementType A[], int N)
{
    ElementType *TmpA;
    TmpA = malloc(N*sizeof(ElementType));
    if(TmpA != NULL) {
        while(length < N) {
            Merge_pass(A, TmpA, N, length);
            length *= 2;
            Merge_pass(TmpA, A, N, length);
            length *= 2;
        }
        free(TmpA);
    } else
        Error("Sapce not enough");
}