凸包(Convex Hull)是一个计算几何(图形学)中的概念。
在一个实数向量空间V中,对于给定集合X,所有包含X的凸集的交集S被称为X的凸包。
X的凸包可以用X内所有点(X1,...Xn)的线性组合来构造.
在二维欧几里得空间中,凸包可想象为一条刚好包著所有点的橡皮圈。
用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边型,它能包含点集中所有的点。
例子:假设平面上有p0~p12共13个点,过某些点作一个多边形,使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候,我们就叫它“凸包”。如下图:
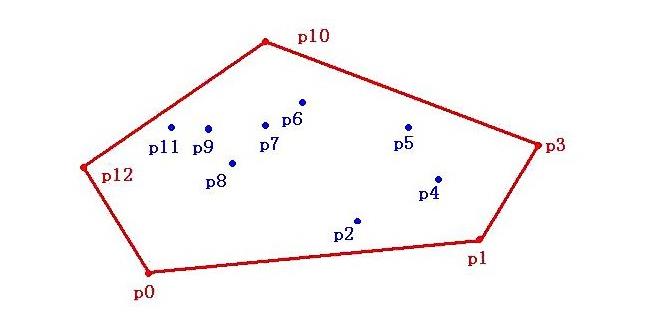

二.解法:
Graham扫描法
时间复杂度:O(n㏒n)
思路:Graham扫描的思想是先找到凸包上的一个点,然后从那个点开始按逆时针方向逐个找凸包上的点,实际上就是进行极角排序,然后对其查询使用。 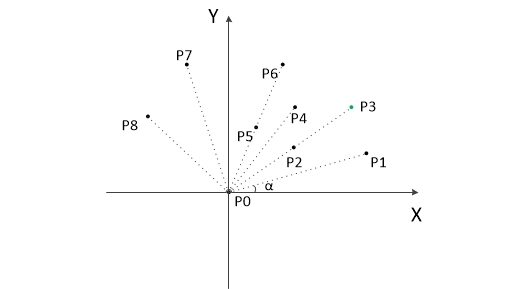
步骤:
- 把所有点放在二维坐标系中,则纵坐标最小的点一定是凸包上的点,如图中的P0。
- 把所有点的坐标平移一下,使 P0 作为原点,如上图。
- 计算各个点相对于 P0 的幅角 α ,按从小到大的顺序对各个点排序。当 α 相同时,距离 P0 比较近的排在前面。例如上图得到的结果为 P1,P2,P3,P4,P5,P6,P7,P8。我们由几何知识可以知道,结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
(以上是准备步骤,以下开始求凸包)
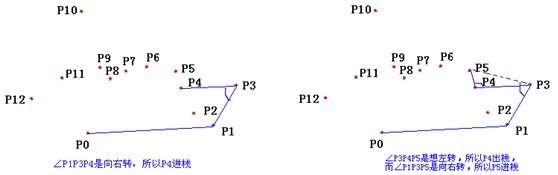
以上,我们已经知道了凸包上的第一个点 P0 和第二个点 P1,我们把它们放在栈里面。现在从步骤3求得的那个结果里,把 P1 后面的那个点拿出来做当前点,即 P2 。接下来开始找第三个点: - 连接P0和栈顶的那个点,得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5;如果在直线上,或者在直线的左边就执行步骤6。
- 如果在右边,则栈顶的那个元素不是凸包上的点,把栈顶元素出栈。执行步骤4。
- 当前点是凸包上的点,把它压入栈,执行步骤7。
- 检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点,返回步骤4。
最后,栈中的元素就是凸包上的点了。
以下为用Graham扫描法动态求解的过程: 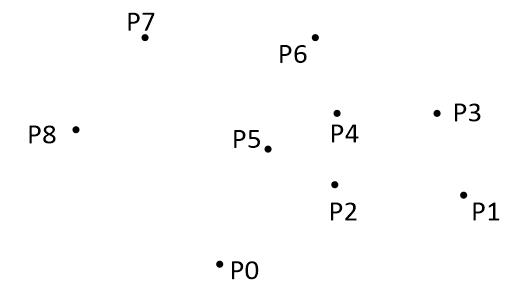
下面静态求解过程
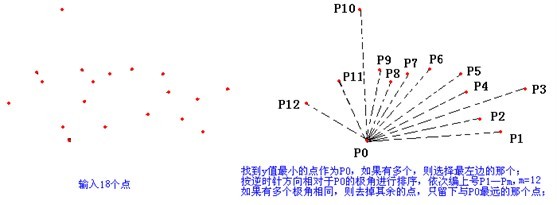




三.模板
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #define PI 3.1415926535 using namespace std; struct node { int x,y; }; node vex[1000];//存入的所有的点 node stackk[1000];//凸包中所有的点 int xx,yy; bool cmp1(node a,node b)//排序找第一个点 { if(a.y==b.y) return a.x<b.x; else return a.y<b.y; } int cross(node a,node b,node c)//计算叉积 { return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y); } double dis(node a,node b)//计算距离 { return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y)); } bool cmp2(node a,node b)//极角排序另一种方法,速度快 { if(atan2(a.y-yy,a.x-xx)!=atan2(b.y-yy,b.x-xx)) return (atan2(a.y-yy,a.x-xx))<(atan2(b.y-yy,b.x-xx)); return a.x<b.x; } bool cmp(node a,node b)//极角排序 { int m=cross(vex[0],a,b); if(m>0) return 1; else if(m==0&&dis(vex[0],a)-dis(vex[0],b)<=0) return 1; else return 0; /*if(m==0) return dis(vex[0],a)-dis(vex[0],b)<=0?true:false; else return m>0?true:false;*/ } int main() { int t,L; while(~scanf("%d",&t),t) { int i; for(i=0; i<t; i++) { scanf("%d%d",&vex[i].x,&vex[i].y); } if(t==1) printf("%.2f\\n",0.00); else if(t==2) printf("%.2f\\n",dis(vex[0],vex[1])); else { memset(stackk,0,sizeof(stackk)); sort(vex,vex+t,cmp1); stackk[0]=vex[0]; xx=stackk[0].x; yy=stackk[0].y; sort(vex+1,vex+t,cmp2);//cmp2是更快的,cmp更容易理解 stackk[1]=vex[1];//将凸包中的第两个点存入凸包的结构体中 int top=1;//最后凸包中拥有点的个数 for(i=2; i<t; i++) { while(i>=1&&cross(stackk[top-1],stackk[top],vex[i])<0) //对使用极角排序的i>=1有时可以不用,但加上总是好的 top--; stackk[++top]=vex[i]; //控制<0或<=0可以控制重点,共线的,具体视题目而定。 } double s=0; //for(i=1; i<=top; i++)//输出凸包上的点 //cout<<stackk[i].x<<" "<<stackk[i].y<<endl; for(i=1; i<=top; i++) //计算凸包的周长 s+=dis(stackk[i-1],stackk[i]); s+=dis(stackk[top],vex[0]);//最后一个点和第一个点之间的距离 /*s+=2*PI*L; int ans=s+0.5;//四舍五入 printf("%d\\n",ans);*/ printf("%.2lf\\n",s); } } }
