数据结构—各类‘排序算法’实现（下）

Posted 2020-07-11

       在上一篇博客中，主要是实现各种的排序算法，并针对一些算法进行了优化的处理，下面主要讨论一下非比较排序的算法（计数排序、基数排序），同时并对各种排序算法的性能、时间复杂度、空间复杂度、优缺点、以及适用场景做总结分析。

1.计数排序

         主要思想：主要是需要统计次数，使用直接定址法，统计最大数和最小数，开辟两个数相差的空间大小，对于重复数据，使用count用来计数,时间复杂度O(N+范围个数)，空间复杂度O(范围个数)计数排序适合于数据较为密集的情况，当数据密集且没有重复的数据，可以直接使用‘位图’，更能够省下空间

void CountSort(int* a, size_t size)
{
     assert(a);
     int max = a[0];
     int min = a[0];
     int count = 0;
 
     for (size_t i = 0; i < size; ++i)      //寻找数组中的最大数和最小数
     {
          if (a[i] < min)
          {
               min = a[i];
          }
          if (a[i] > max)
          {
               max = a[i];
          }
     }
     
     int* tmp = new int[max - min + 1];    //开辟存储空间,并初始化
     memset(tmp, 0, sizeof(int)*(max - min + 1));
     for (size_t i = 0; i < max - min + 1; ++i)   //直接定址法
     {
          int num = a[i] - min;
          tmp[num]++;
     }
     for (size_t i = 0; i < size;)    //将排序好的顺序写入a数组中
     {
          for (size_t j = 0; j < max - min + 1; ++j)
          {
               count = tmp[j];
               while (count--)    //对于重复数据需要多次进行写入
               {
                    a[i] = j + min;
                    i++;
               }
          } 
     }
     delete[] tmp;
}

2.基数排序

        主要思想：和‘快速转置’的思想相像，开辟两个数组count和start，count用来统计个位上分别为0~9的数据个数，start用来统计数据的开始位置（起始位置为0，下一位的数据开始的位置=上一个数据的开始位置+上一位总的数据个数），另开辟size大小的空间来存放每次排序，下面是低位基数排序，从个位开始排序，然后排序十位，进而百位，直到排到最大数据的最高位，排序结束。

int GetMaxRadix(int* a, size_t size)    //寻找最大数据的位数
{
     int index = 1;   //数据最小有一位
     int max = 10;
     for (size_t i = 0; i < size; ++i)
     {
          while (a[i] >= max)      //数据大于1位
          {
               index++;
               max = max * 10;
          }
     }
     return index;
}

void LSDSort(int* a, size_t size)
{
     assert(a);
     int index = GetMaxRadix(a, size);   //求最大数据的位数
     int count[10] = { 0 };    //记录数据出现的次数
     int start[10] = { 0 };   //记录数据的开始位置
     int radex = 1;
     int* bucket = new int[size];   
     
     for (int k = 1; k <= index; ++k)    //从各位到最高位排序
     {
          memset(count, 0, sizeof(int)* 10);    //每次排序之前需将count置0
          //计数（各位分别为0~9的数据个数）
          for (size_t i = 0; i < size; ++i)
          {
               int num = (a[i] / radex) % 10;     //取个位
               count[num]++;
          }
          
          //记录数据开始的位置
          start[0] = 0;
          int j = 1;
          while (j < 10)
          {
               start[j] = start[j - 1] + count[j - 1];
               j++;
          }
          for (size_t i = 0; i < size; ++i)   //将数据按顺序放入bucket中
          {
               int num = (a[i] / radex) % 10;
               bucket[start[num]++] = a[i];
          }
          radex *= 10;
          memcpy(a, bucket, sizeof(int)* size);
     }    
     delete[] bucket;
}

3.排序算法总结

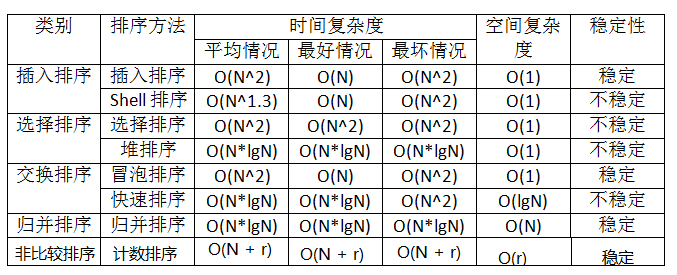
（1）各种排序算法的性能分析

 其中：r为数据范围的个数 

稳定性分析：

        稳定性：指的是需要排序的数据之中如果有相同的数据元素，在排序前、后的相对位置是不变的，即就是当排序{1,3,5,7,2,5,6}，通过排序后‘5’在‘5‘之前，而不是相互交换了。

         在介绍的这几种排序之中插入排序、冒泡排序、归并排序、计数排序是稳定的。快速排序、希尔排序、选择排序、堆排序是不稳定的

空间复杂度：

        排序算法中，快速排序（需要进行递归）、归并排序、计数排序、基数排序都是需要额外的空间进行排序。其余的排序算法就不需要借助任何的空间。

时间复杂度：

 O(N^2)：

        插入排序、冒泡排序、选择排序都是空间复杂度为O(N^2)，排序效率基本上都是比较低，选择排序是最不好的，因为在最有的情况下，也需要N^2的时间复杂度，相对来说，插入和冒泡能好一点，在优化的情况下，能够减少排序的时间。但是当数据量较大时，冒泡的时间代价会更高。

O(N*lgN)：

       平均性能为O(N*lgN)的算法：快速排序、归并排序、堆排序算法，快速排序经过各种的优化算法（三数取中法、区间较小时利用直接插入算法，【上篇博客中详细的介绍了快速排序的优化】）已经相对来说效率提高了很多。

       归并排序又称为外排序，外排序其实就是指能够对内存之外（磁盘中）数据进行排序，对于大数据的文件，不能够直接加载到内存中进行排序，我们可以采取将文件划分成小文件，将小的文件加载到内存中进行排序，然后将排好序的数据进行重写，将两个有序的数据文件在重新排序，就能够排好大数据文件。这个读者可以下去进行试验，这里就不做详细的解释。

       堆排序的效率虽然还是挺高的，但是堆排序有个致命的缺点，就是只能够对数组进行排序，因为需要通过数组的下标来确定数据在堆中的具体位置。所以堆排序只能对数组进行排序。

本文出自 “无心的执着” 博客，请务必保留此出处http://10740590.blog.51cto.com/10730590/1782091