注:该部分参考kaggle房价模型的大神Pedro Marcelino提供的kernel
在我们拿到数据后,应该预先分析一下数据。
1、总览数据
import numpy as np
import pandas as pd
df_train=pd.read_csv(\'train.csv\')
df_train.head()#结果在这里不展示
通过以上可以对数据有大体的了解,会发现既有数值型数据,也有类别型数据。注意区别。
df_train.columns#展示各列的名字
2、对特定列进行分析
df_train[\'SalePrice\'].describe()#研究房价(target),即结果一列,会显示该列的均值 方差 标准差 四分位数 最值等信息
and
#对最后一列的数据做可视化
import seaborn as sns
import matplotlib.pyplot as plt
sns.distplot(df_train[\'SalePrice\'])
plt.show()
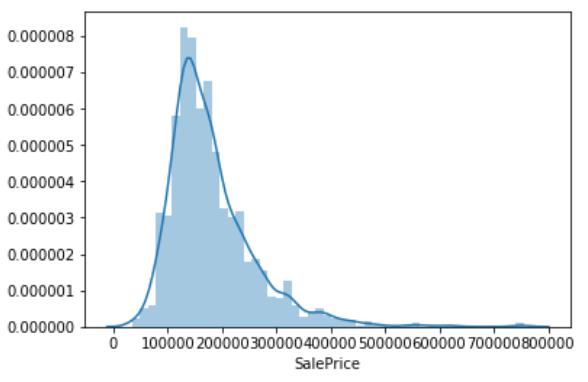
#skewness and kurtosis
print("Skewness: %f" % df_train[\'SalePrice\'].skew())
print("Kurtosis: %f" % df_train[\'SalePrice\'].kurt())
#Skewness: 1.882876 Kurtosis: 6.536282
偏度(skewness)也称为偏态、偏态系数,是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。
峰度(peakedness;kurtosis)又称峰态系数。表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来,峰度反映了峰部的尖度。
3、分析某个元素与结果列(saleprice)的关系
#scatter plot grlivarea/saleprice即研究某个特征与房价的关系
var = \'GrLivArea\'
data = pd.concat([df_train[\'SalePrice\'], df_train[var]], axis=1)
data.plot.scatter(x=var, y=\'SalePrice\', ylim=(0,800000));
plt.show()
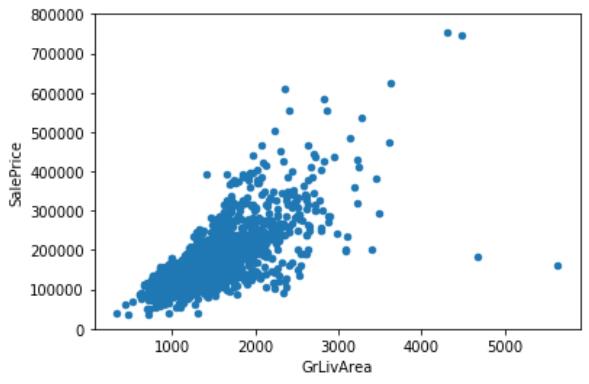
#检查另一个特征与房价的关系
var=\'TotalBsmtSF\'
data=pd.concat([df_train[\'SalePrice\'],df_train[var]],axis=1)
data.plot.scatter(x=var,y=\'SalePrice\',ylim=(0,800000))
plt.show()
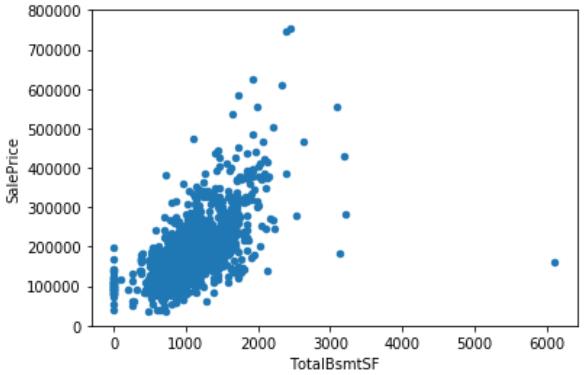
注意,以上两个是对数值型数据的分析,下面是类别型数据的分析。
#以上都是数值型数据与房价的分布,下面时类别型数据与房价的分布描述
#box plot overallqual/saleprice
var = \'OverallQual\'
data = pd.concat([df_train[\'SalePrice\'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
plt.show()
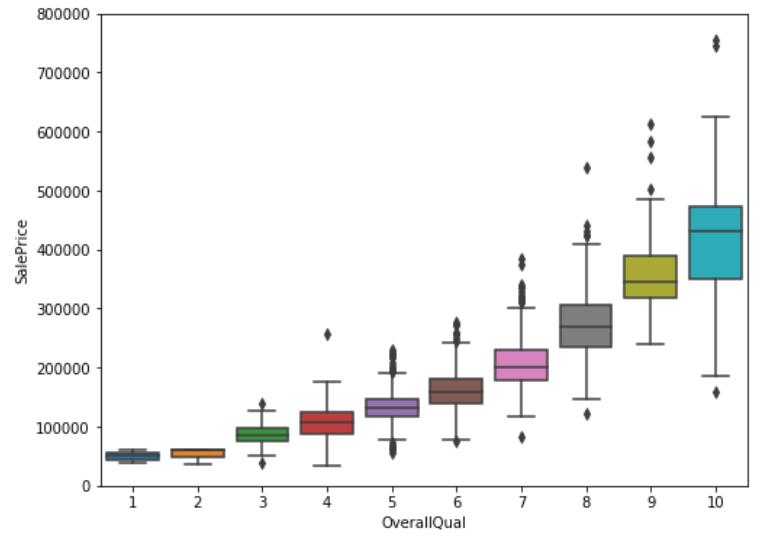
分析这张图:在这里我们使用的是箱型图(盒图),主要包含六个数据节点,将一组数据从大到小排列,分别计算出上边缘,上四分位数Q3,中位数,下四分位数Q1,下边缘,分散的是异常值。上下边缘之间是正常数据的分布区间
#类别型数据
var = \'YearBuilt\'
data = pd.concat([df_train[\'SalePrice\'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000)
plt.xticks(rotation=90)
plt.show()
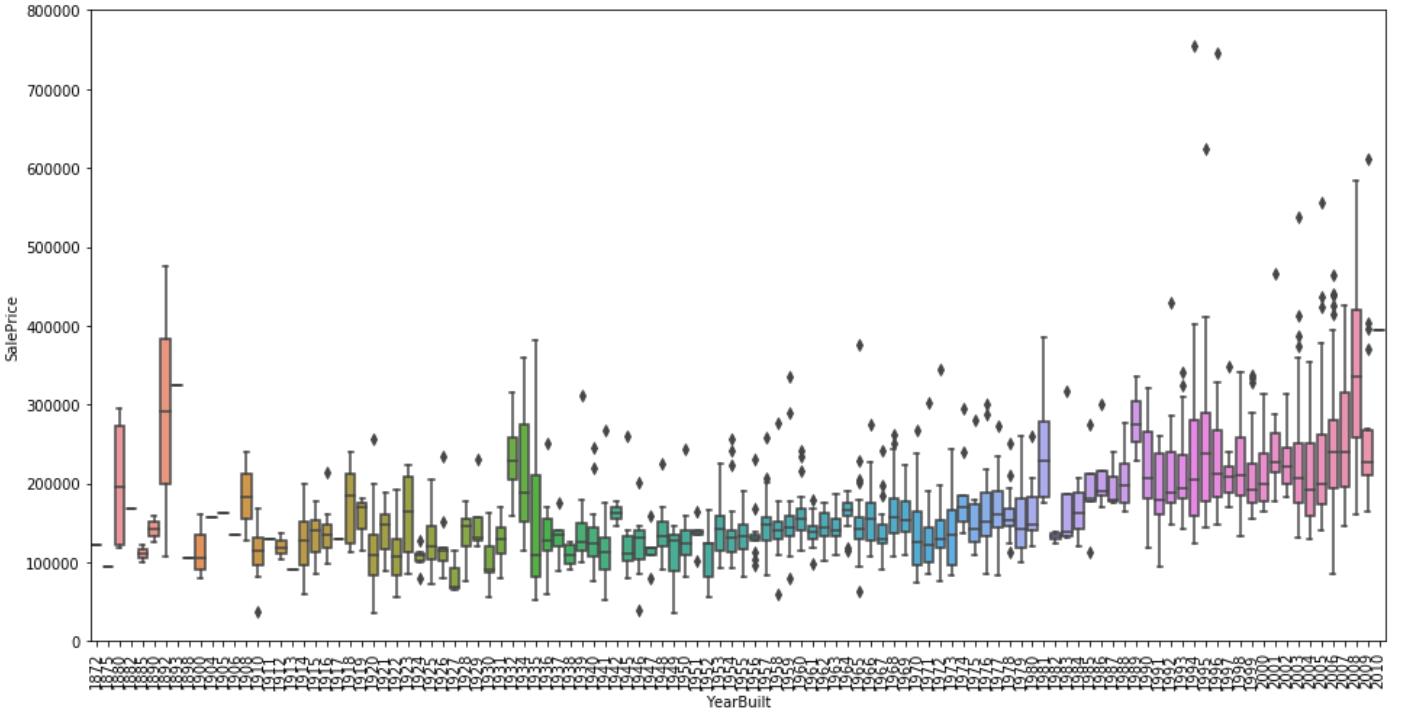
相关性的分析:
#correlation matrix相关矩阵
corrmat = df_train.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True)
plt.show()
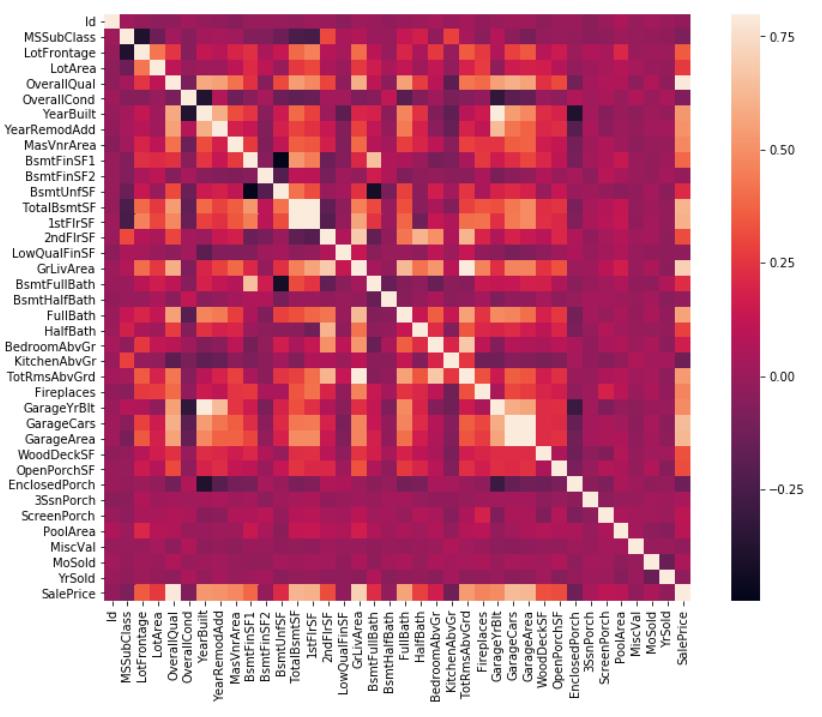
分析:相关矩阵可以用颜色和数值表示任意两个元素之间的相关性,颜色越淡,表示相关性越强,反之相关性越弱,可参考colorbar。
#saleprice correlation matrix 相关矩阵
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, \'SalePrice\')[\'SalePrice\'].index
cm = np.corrcoef(df_train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt=\'.2f\', annot_kws={\'size\': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
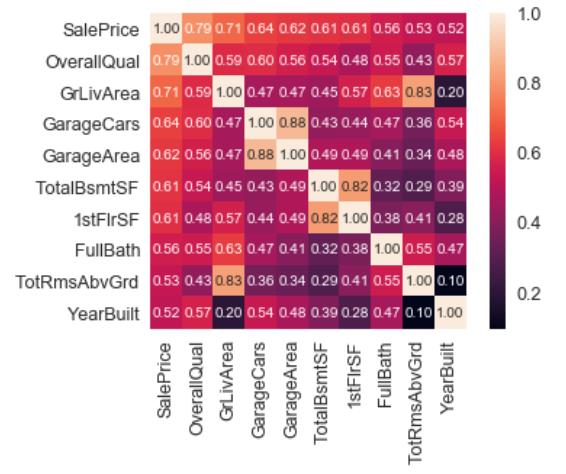
分析:两个相同元素之间的相关性是1,如saleprice与saleprice,另外从图中我们看到garagecars与garagearea的相关性在0.88,表明这两个元素相关性很强,因此在后面做数据分析(机器学习)时,可以只取其中一个元素特征即可。相似的还有totalbsmtSF与1stFlrSF。同时,如果一个特征与saleprice之间的相关性很弱,那么这个特征可以舍去。
#scatterplot
sns.set()
cols = [\'SalePrice\', \'OverallQual\', \'GrLivArea\', \'GarageCars\', \'TotalBsmtSF\', \'FullBath\', \'YearBuilt\']
sns.pairplot(df_train[cols], size = 2.5)
plt.show()
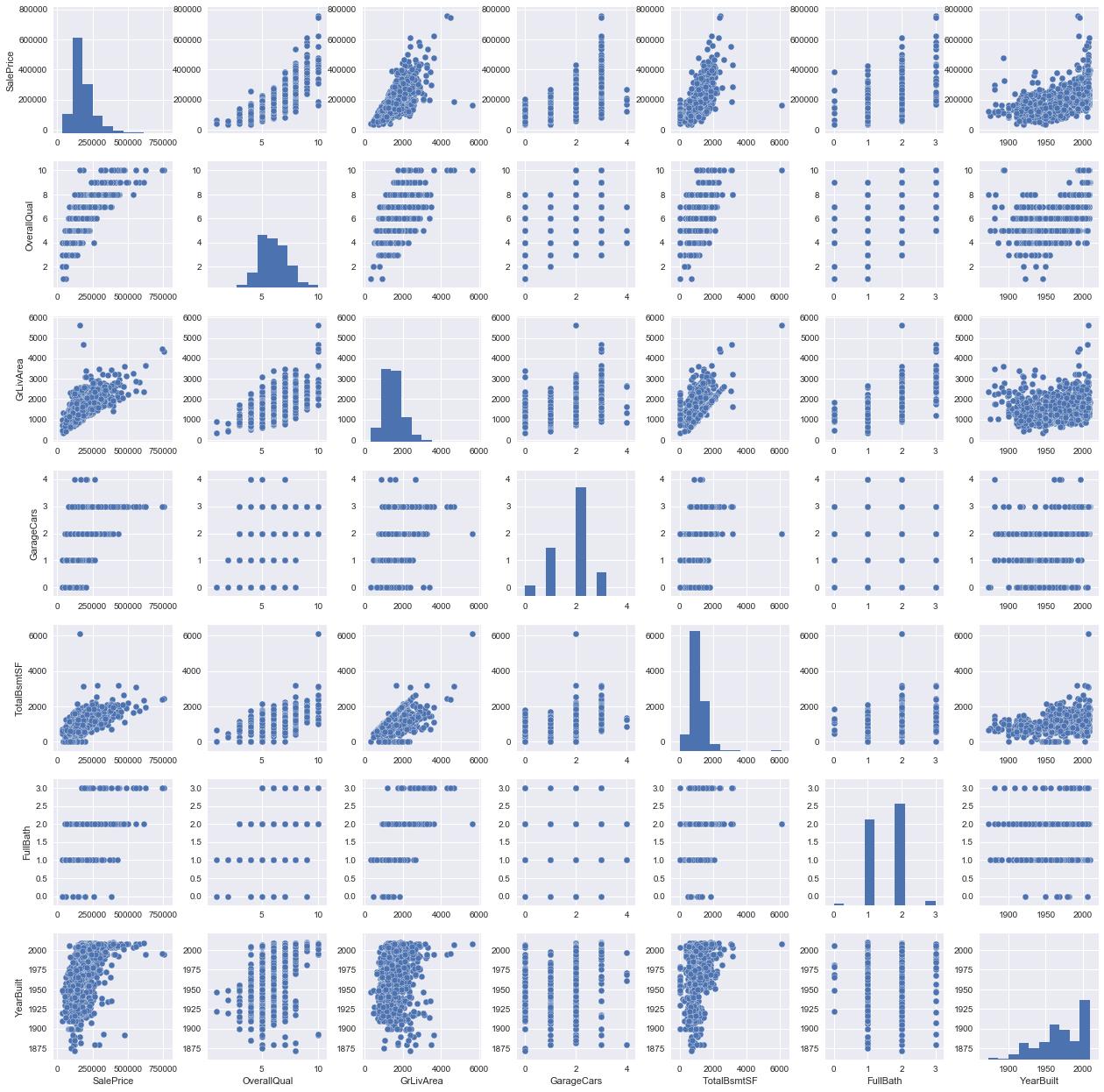
分析: