2018BNU校赛总决赛
Posted hk lin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2018BNU校赛总决赛相关的知识,希望对你有一定的参考价值。
题解是qls的题解我就懒得写了23333
A塞特斯玛斯塔
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
题目描述
quailty是一名狂热的ACM音游选手,沉迷各种音乐游戏,比如Lunatic Rave 2,osu!之类的。
今天,quailty玩的是国内游戏厂商雷亚(并不是赞助商)出品的一款音乐游戏Cytus。
游戏中,玩家需要随着游戏界面中上下移动的扫描线来适时演奏对应音符。
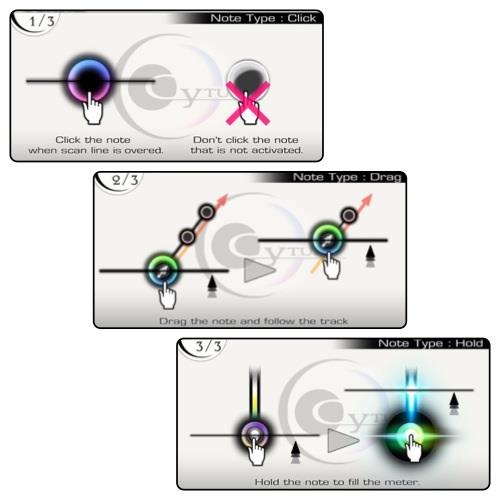
当上下移动的黑色线(扫描线)与圆形的物体(音符)的圆心重合时点击音符。
普通音符(图中第一种)只需点击即可。
锁链音符(图中第二种)将带箭头的音符(滑块)按下后不要松开,并将滑块沿着斜线和圆点组成的路径拖动,直至拖动到最后一个圆点处方可松开。注意拖动过程中应保持滑块圆心始终与扫描线重合。
长按音符(图中第三种)按下后不要松开,原地不动,等扫描线到达其末端并显示判定结果后方可松开。
Cytus共有五种判定,从好到坏依次为:彩PERFECT、黑PERFECT、GOOD、BAD、MISS。
得分中包括了90%的“判定分”和10%的“连击分”,而连击分是累进计算的,断COMBO对其影响很大,往往只要有1个MISS就会损失几万的连击分。
彩PERFECT和黑PERFECT在计算得分时一视同仁,只要全部PERFECT即可获得满分,满分为1000000,被称为MILLION Master。
quailty真的很严格,如果打完一把没有拿到MILLION Master,他就认为自己是NAIVE Noob。
现在给你quailty打出的判定序列,请你输出这次游戏的评价是MILLION Master还是NAIVE Noob。
输入描述:
第一行是一个正整数T ( 1 ≤ T ≤ 5 ),表示测试数据的组数,
每组测试数据,第一行是一个正整数n ( 1 ≤ n ≤ 100000 ),表示该组测试数据包含的判定数。接下来的n行,每行包含"PERFECT"、"GOOD"、"BAD"、"MISS"之中的一个字符串,表示quailty打出的一个判定。
输出描述:
对于每组数据,输出一行,包含一个字符串,表示这次游戏的评价。
输入
2 5 PERFECT PERFECT PERFECT PERFECT PERFECT 10 PERFECT MISS PERFECT BAD BAD GOOD BAD GOOD GOOD MISS
输出
MILLION Master NAIVE Noob
判断是不是全是perfect。

1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 #define mp(x,y) make_pair(x,y) 8 using namespace std; 9 const int N=1e5+10; 10 int n,m,flag,T; 11 char s[N],ans[]="PERFECT"; 12 int main() 13 { 14 scanf("%d",&T); 15 while(T--) 16 { 17 scanf("%d",&n); 18 flag=1; 19 for(int i=1;i<=n;i++) 20 { 21 scanf("%s",s); 22 if(strcmp(s,ans)!=0) 23 flag=0; 24 } 25 if(flag) 26 printf("MILLION Master\\n"); 27 else 28 printf("NAIVE Noob\\n"); 29 } 30 return 0; 31 }
B 外挂使用拒绝
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
题目描述
ATG5是ATG系列最新作,游戏故事发生以美国洛杉矶及其周边地区为原型的城市Sos Lantos,是现实地区中的洛杉矶和南加州。制作单位拍摄了超过25万张相关照片,并且研究了人口调查和汽车销售数据,以建立游戏中的世界。
ATG系列历来都是以黑帮生活为背景的知名动作冒险游戏。主人公自然与黑道脱不了干系,在ATG5中游戏元素将会得到增强,加入了更加开放自由的世界,以故事驱动,以任务为准的游戏玩法和多人模式。故事主题聚焦金钱永不眠的南加利福尼亚。这次作品是有史以来最具活力的和最多元化的开放式世界,作为玩家可以反复进入三个角色的生活,玩交织在一起的所有内容。
ATG5这款游戏质量很高,但是外挂猖獗。。。
最近,三七开发现了一款神奇的外挂,可以让他在多个账号之间转移金钱。
神奇外挂的神奇不止于此,当他把一个账号的金钱转移到另一个账户时,原来账户里的金钱并不会减少!是不是很神奇?
三七开一共有n个账号,每一天他都会通过这个神奇外挂把第1个账号的金钱“转移”到第2个账号,再把第2个账号的金钱“转移”到第3个账号,……,再把第n-1个账号的金钱“转移”到第n个账号。
但是三七开忘了一件事情,游戏中金钱数量是有上限的,每当一个账号的金钱数大于等于1000000007(=109+7)时,这个账号的金钱数就会对109+7取模,即变成金钱数除以109+7的余数。尽管如此,三七开还是很开心地继续使用着他的神奇外挂,并且没有花账号里的一分金钱。
然而,在三七开使用了k天神奇外挂之后,B星公司(ATG5的发行公司)发现了他的开挂行为。B星公司对使用外挂行为非常仁慈,决定不对三七开进行封号处理,而是将三七开的所有账号的金钱数恢复至他开挂以前的数值。但服务器并没有关于那么久远的数据的存档,只有现在的金钱数的数据,以及检测到的开挂天数k。
你能帮助B星公司恢复三七开的账号数据吗?
输入描述:
第一行是一个正整数T(T ≤ 15),表示测试数据的组数,
对于每组测试数据,
第一行包含两个整数n(2 ≤ n ≤ 1000),k(0 ≤ k ≤ 100000000),表示账号个数和开挂天数,
第二行包含n个小于109+7的非负整数,第i个整数表示当前第i个账号的金钱数。
输出描述:
对于每组测试数据,输出一行,包含n个以空格分隔的非负整数(每个数范围小于109
+7,注意不要有行末空格),第i个整数表示开挂前第i个账号的金钱数。
输入
2 3 1 3 2 1 4 2 1 2 1 2
输出
3 1000000006 1000000006 1 0 1000000005 2
连加和连减这一类的都可以从杨辉三角找找规律2333,找找规律就能出通项了。



1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 #define mp(x,y) make_pair(x,y) 8 using namespace std; 9 const int N=1e3+10; 10 LL a[N]; 11 LL fac[N],inv[N]; 12 LL ans[N],k; 13 int T,n,m,tk; 14 LL quickpow(LL x,LL n) 15 { 16 LL ans=1; 17 x%=mod; 18 while(n) 19 { 20 if(n&1) ans=ans*x%mod; 21 n>>=1; 22 x=x*x%mod; 23 } 24 return ans; 25 } 26 void init(int n,LL k) 27 { 28 fac[0]=1; 29 LL p=1; 30 for(int i=1;i<=n && k>=0;i++,k--) 31 fac[i]=fac[i-1]*k%mod; 32 for(int i=1;i<=n;i++) 33 p=p*i%mod; 34 inv[n]=quickpow(p,mod-2); 35 for(int i=n-1;i>=0;i--) 36 inv[i]=inv[i+1]*(i+1)%mod; 37 return ; 38 } 39 LL comb(LL k,int n) 40 { 41 if(1LL*n>k) 42 return 0; 43 else 44 return (fac[n]*inv[n])%mod; 45 } 46 int main() 47 { 48 scanf("%d",&T); 49 while(T--) 50 { 51 scanf("%d%lld",&n,&k); 52 for(int i=1;i<=n;i++) 53 scanf("%lld",a+i); 54 init(n,k); 55 clr(ans); 56 for(int i=1;i<=n;i++) 57 { 58 tk=-1; 59 m=-1; 60 for(int j=i;j>=1;j--) 61 { 62 tk++; 63 m=-m; 64 ans[i]=((ans[i]+comb(k,tk)*m%mod*a[j]%mod)%mod+mod)%mod; 65 } 66 } 67 for(int i=1;i<n;i++) 68 printf("%lld ",ans[i]); 69 printf("%lld\\n",ans[n]); 70 } 71 return 0; 72 }
C 萌萌哒身高差
空间限制:C/C++ 32768K,其他语言65536K
Special Judge, 64bit IO Format: %lld
题目描述
“清明时节雨纷纷,路上行人欲断魂。”
然而wfy同学的心情是愉快的,因为BNU ACM队出去春游啦!并且,嗯。。。
以下是wfy同学的日记:
昨天,何老师告诉我们:明天我们去春游,大家准备好喝的和吃的哦!
大家听了都兴奋起来,有的欢呼,有的鼓掌,开心得不得了。第二天,我们早早地来到学校,迫不及待地上了车,来到了公园。一进门,啊,太美了!公园中有那么多树,有高有矮,有粗有瘦,密密的,在春风吹拂下轻轻摇摆着,像是欢迎我们的到来。公园中有那么多的鲜花,有红有黄,有紫有白,散发着淡淡的清香,闻得我们都醉了。公园的边角上有一条清澈的小河,河水缓缓地流淌着,可以看到水里的鱼儿在快活地游来游去,多自在啊!水草碧绿碧绿的,多新鲜啊!小河的旁边是一片小树林,远远望去一片鲜绿。我们在里面吃东西、做游戏、捉迷藏,玩得疯极了。树林的后面是连绵起伏的小山坡,蜿蜿的真像一条游动的蛇。当然,我觉得公园的天空也很美。它万里无云,一碧如洗,很清澈。小鸟在展翅飞翔,它们形态各异,一会儿上升,一会儿下滑,一会儿吃虫,一会儿在小树林里休息,非常悠闲。快乐时光总是那么短暂,很快,天色就昏暗了。我们依依不舍地上了车,回到了学校,我真希望明年的春天还能再来看看这美丽的公园。
回到学校后,何老师说:请大家排成一排,我们来拍照片啦!
何老师特别喜欢萌的东西,比如**,比如****,等等。
何老师认为,同学们站成一排时,相邻两个同学身高相差越多,这两个同学站在一起越萌。
那么所有相邻两个同学的身高差加起来越大,拍出来的照片就越萌,也就是这张照片的萌力指数。
何老师希望拍出来的照片的萌力指数尽可能大。
然而何老师并不是数学老师,而是语文老师。何老师觉得很GG。
何老师只想知道,如果让同学们随便站成一排(站成所有排列的可能性都相等),萌力指数的数学期望是多少。
聪明的我一下子就算出了答案,然后何老师就奖励了我一个很萌的礼物。
今天真的好开心。
BNU ACM队共有n名同学,身高分别是,聪明的你能计算出何老师想要的数学期望吗?
输入描述:
第一个是一个正整数T(T ≤ 20),表示测试数据的组数,
每组测试数据只有一行,包含一个整数n(2 ≤ n ≤ 100)。
输出描述:
对于每组测试数据,输出一行,包含一个实数,表示萌力指数的数学期望值,要求相对误差不超过,
也就是说,令输出结果为a,标准答案为b,若满足,则输出结果会被认为是正确答案。
输入
2 2 3
输出
1.000000000000 2.666666666667
说明
对于第二组样例,所有可能的排列是[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1],所以答案是
嗯找找规律写个第四第五项就可以发觉是 $ \\frac{n^2-1}{3} $ 。别去推了,我推了半天还推错了orz。赛后推出来了太麻烦,不如猜公式。就是从上一个n-1的排列去推加进去一个n以后增加了多少,那么f[n]=[n-1]+一个计算n加进去后期望增加的贡献。可以通过固定右端的数字然枚举左端的数字来算,然后还有左端没有以及右端没有总共三种情况。概率就相当于出现总数除总排列数。


1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 #define mp(x,y) make_pair(x,y) 8 using namespace std; 9 const int N=1e2+10; 10 int T,n,m,all; 11 LL a[N],pre[N]; 12 double ans[N]; 13 void init(int n) 14 { 15 a[1]=1; 16 ans[1]=0; 17 for(int i=2;i<=n;i++) 18 { 19 a[i]=a[i-1]+2; 20 pre[i]=pre[i-1]+a[i]; 21 ans[i]=1.0*pre[i]/3; 22 } 23 return ; 24 } 25 int main() 26 { 27 init(100); 28 scanf("%d",&T); 29 while(T--) 30 { 31 scanf("%d",&n); 32 printf("%.10f\\n",ans[n]); 33 } 34 return 0; 35 }
D 雷电爆裂之力
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
题目描述
输入描述:
第一行是一个正整数T(≤ 20),表示测试数据的组数,
对于每组测试数据,
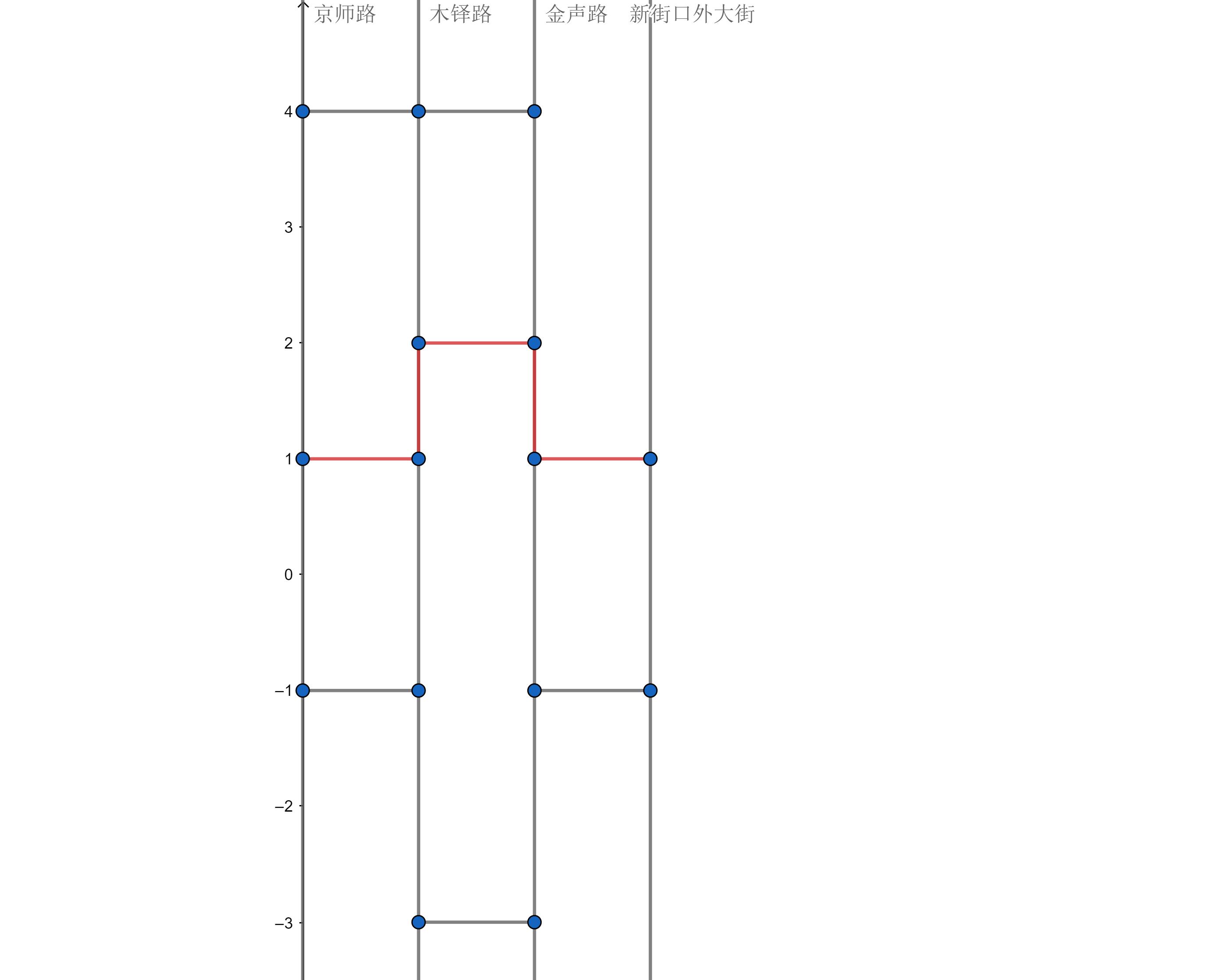
第一行是一个整数n,m,k(1≤ n,m,k ≤ 100000),分别表示连接京师路与木铎路,木铎路与金声路,金声路与新街口外大街的道路个数,
第二行包含n个以空格分隔的整数a1,a2,...,an,表示连接京师路与木铎路的各个小道的南北方向坐标(单位:m),
第三行包含m个以空格分隔的整数b1,b2,...,bm,表示连接木铎路与金声路的各个小道的南北方向坐标(单位:m),
第四行包含k个以空格分隔的整数c1,c2,...,ck,表示连接金声路与新街口外大街的各个小道的南北方向坐标(单位:m),
保证每行坐标按严格递增的顺序给出,并且坐标绝对值不超过109。
输出描述:
对于每组测试数据,输出一行,包含一个整数,表示答案(单位:s)。
输入
1 3 3 2 -1 1 4 -3 2 4 -1 1
输出
5
序都给你排好了,你就枚举中间那条路的所有路位置,然后双指针指向前面和后面两边的路去做,O(n)的。

#include<bits/stdc++.h> #define clr(x) memset(x,0,sizeof(x)) #define clr_1(x) memset(x,-1,sizeof(x)) #define LL long long #define INF 0x3f3f3f3f using namespace std; const int N=1e5+10; int n,m,k; LL a[N],b[N],c[N]; int T,lt,rt; LL ans,pt; int main() { scanf("%d",&T); while(T--) { scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=n;i++) scanf("%lld",a+i); for(int i=1;i<=m;i++) scanf("%lld",b+i); for(int i=1;i<=k;i++) scanf("%lld",c+i); ans=abs(a[1]-b[1])+abs(b[1]-c[1]); lt=rt=1; for(int i=1;i<=m;i++) { while(lt<n && a[lt]<b[i]) lt++; while(rt<k && c[rt]<b[i]) rt++; pt=0; if(lt>1) pt+=min(abs(a[lt]-b[i]),abs(a[lt-1]-b[i])); else pt+=abs(a[lt]-b[i]); if(rt>1) pt+=min(abs(c[rt]-b[i]),abs(c[rt-1]-b[i])); else pt+=abs(c[rt]-b[i]); ans=min(ans,pt); } printf("%lld\\n",ans+3); } return 0; }
E 可以来拯救吗
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
题目描述
quailty is BNU\'s red sun.
quailty非常喜欢给同学讲题,一天,他又拉着SK给他讲题。
quailty:给一个长为n的序列,求给定子序列的和,会吗?
SK:。。
quailty:给一个长为n的序列,求给定子序列的和的平方,会吗?
SK:。。。
quailty:给一个长为n的序列,求所有子序列的和的平方和,会吗?
SK:。。。。。
quailty:给一个长为n的序列,求所有长为k的子序列的和的平方和,会吗?
SK:。。。。。。。。
quailty:给一个长为n的序列,求所有长为k的子序列的和的平方的异或和,会...
SK:我^(^&*((^%^#……
SK拔出了他的40m长刀,场面就快控制不住了,请你赶快来做出这道题,拯救一下quailty。
quailty is BNU\'s red sun.
输入描述:
第一行是一个正整数T(≤ 10),表示测试数据的组数,
对于每组测试数据,
第一行是两个正整数n,k(k ≤ n ≤ 100000),分别表示序列长度和需要考虑的子序列长度,
接下来一行包含n个不超过1000的正整数,表示序列的n个元素,
为了简化问题,保证,也就是说,需要考虑的子序列不超过100000个。
输出描述:
对于每组测试数据,输出一行,包含一个整数,表示所有长为k的子序列的和的平方的异或和。
输入
1 4 2 1 2 3 4
输出
12
说明
对于样例,长度为2的子序列有[1,2],[1,3],[1,4],[2,3],[2,4],[3,4],所以答案是9^16^25^25^36^49=12(这里\'^\'是C++中的异或运算符)。
dfs暴力枚举所有会出现的序列,因为他保证考虑的序列不超过$ 10^6 $个。同时n最长为1000,所以没事的能过。要注意的是一旦 $ k> \\frac{a}{2} $ 那么我们考虑的序列应该是 $ n-k $ 的序列,然后拿总和减掉这个序列和就行了。


1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define LL long long 5 #define INF 0x3f3f3f3f 6 using namespace std; 7 const int N=1e5+10; 8 LL a[N]; 9 int n,k,T; 10 bool rev; 11 LL all,ans; 12 void dfs(int pt,int now,LL sum) 13 { 14 if(now==k) 15 { 16 if(rev) ans^=(all-sum)*(all-sum); 17 else ans^=sum*sum; 18 return ; 19 } 20 if(n-pt+1<k-now) return ; 21 dfs(pt+1,now,sum); 22 dfs(pt+1,now+1,sum+a[pt]); 23 return ; 24 } 25 int main() 26 { 27 scanf("%d",&T); 28 while(T--) 29 { 30 scanf("%d%d",&n,&k); 31 all=0; 32 rev=0; 33 ans=0; 34 for(int i=1;i<=n;i++) 35 { 36 scanf("%lld",a+i); 37 all+=a[i]; 38 } 39 if(k>n/2) 40 { 41 rev=1; 42 k=n-k; 43 } 44 dfs(1,0,0); 45 printf("%lld\\n",ans); 46 } 47 return 0; 48 }
F 汤圆防漏理论
空间限制:C/C++ 32768K,其他语言65536K
64bit IO Format: %lld
题目描述
ghc很喜欢吃汤圆,但是汤圆很容易被粘(zhān)漏。
根据多年吃汤圆经验,ghc总结出了一套汤圆防漏理论:
互相接触的汤圆容易粘(zhān)在一起,并且接触面积不同,粘(zhān)在一起的粘(nián)度也不同。
当ghc要夹起一个汤圆时,这个汤圆和现在碗里与这个汤圆接触的所有汤圆之间的粘(nián)度的和,如果大于汤圆的硬度,这个汤圆就会被粘(zhān)漏。
今天ghc又要煮汤圆啦,今天要煮n个汤圆,并且摆盘的方法已经设计好:
汤圆按照编号,有m对汤圆互相接触,用xi, yi, zi表示编号为xi和yi的两个汤圆互相接触,粘(nián)度为zi。
汤圆当然是越软越好吃,但是ghc的厨艺只允许把所有汤圆煮成同样的硬度。那么,汤圆的硬度最小可以是多少,可以满足吃的过程中,存在一种夹汤圆的顺序,使得没有汤圆会被粘(zhān)漏呢?
注意:
不考虑汤圆的重力作用;
不能同时夹多个汤圆;
吃完汤圆一定要喝点汤。
输入描述:
第一行是一个正整数T(≤ 5),表示测试数据的组数,
对于每组测试数据,
第一行是两个整数n,m(1≤ n,m≤ 100000),
接下来m行,每行包含三个整数xi, yi, zi(1≤ xi, yi ≤ n, xi ≠ yi, 1 ≤ zi ≤ 1000000),
同一对汤圆不会出现两次。
输出描述:
对于每组测试数据,输出一行,包含一个整数,表示汤圆硬度的最小值。
输入
1 4 6 1 2 2 1 3 2 1 4 2 2 3 3 2 4 3 3 4 5
输出
6
嗯代码我又写挫了。就是每次都贪心的找连边的比边权和最小的删掉。为了这个过程我写了一个记录位置的小根堆然后动态的加入删除。但是记录和维护堆的代码写出来很长的。。然后q巨的做法直接用set一堆代码就省了。


1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 #define mp(x,y) make_pair(x,y) 8 using namespace std; 9 const int N=2e5+10; 10 struct edg 11 { 12 int next,to,val; 13 }edge[N]; 14 int head[N],etot; 15 void addedge(int u,int v,int val) 16 { 17 edge[++etot]=(edg){head[u],v,val}; 18 head[u]=etot; 19 return ; 20 } 21 LL heap[N]; 22 int hashed[N],too[N]; 23 LL val[N],len,ans; 24 int htot,u,v,ve,n,m,T; 25 void init() 26 { 27 clr_1(head);
