第七章 递归函数（续）二分查找算法

Posted 2020-11-03 gnaix

1.递归函数                                                    

递归函数：在函数的内部调用自己

递归的最大深度：998

注意：在编写程序的时候最好不要修改递归深度

　　如果程序需要修改递归深度才能运行，说明这个功能不太适合用递归函数完成

递归函数必须要添加return

递 ---- 函数向深度进行，直到函数不成立 ---> 递归需要有一个停止的条件

归 ---- 值的返回，计算过程

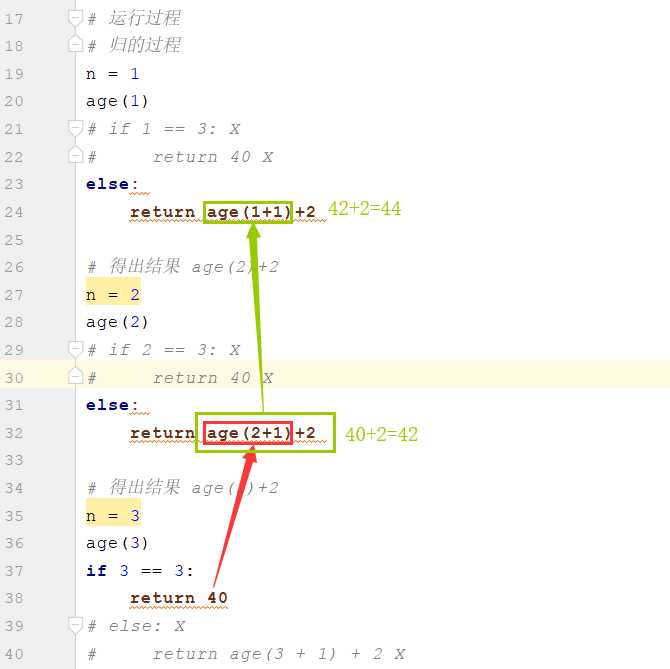
# alex多大了  alex比wusir大两岁  40+2+2
# wusir多大了 wusir比金老板大两岁 40+2
# 金老板多大了 40

def age(n):
    if n == 3:
        return 40
    else:
        return age(n+1)+2

# 运行过程
# 递的过程
n = 1
age(1)
# if 1 == 3: X
#     return 40 X
else:
    return age(1+1)+2

# 得出结果 age(2)+2
n = 2
age(2)
# if 2 == 3: X
#     return 40 X
else:
    return age(2+1)+2

# 得出结果 age(3)+2
n = 3
age(3)
if 3 == 3:
    return 40
# else: X
#     return age(3 + 1) + 2 X

 

2.二分查找算法                                                 

引子：

　　算法：计算一些比较复杂的问题，所采用的 在空间上-（内存里）或者时间上-（执行的时间）更有优势的方法

常见排序算法：快速排序（基础） 堆排序 冒泡（低级）

递归求解二分查找算法：有序的数字集合的查找问题，在l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]中查找66

思路图：

 

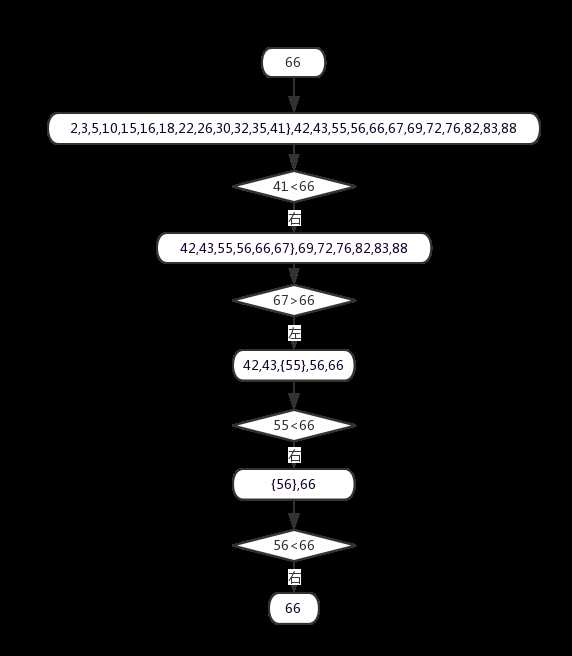
# 算法
def cal(l,num,start=0,end=None):
    # if end is None:end = len(l)-1
    end = len(l)-1 if end is None else end
    if start <= end:
        mid = (end - start)//2 + start
        if l[mid] > num :
            return cal(l, num, start, mid-1)
        elif l[mid] < num:      # 13  24
            return cal(l,num,mid+1,end)
        else:
            return mid
    else:
        return None
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
print(cal(l,66))
# 17