数据结构之二叉树

Posted 2020-11-03 weiziqiang

1.二叉树的基本概念

　　二叉树是一种非常常见并实用的数据结构，它结合了有序数组和链表的优点，在二叉树中查找数据与在数组中查找数据一样快，在二叉树中添加删除数据的速度与在链表中一样高效。

　　二叉树也称为二分树、二元树，对分树等。它是n（n>=0）个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。当集合为空时，该二叉树被称为空二叉树。

　　在二叉树中，一个元素也被称为结点。另外，二叉树的递归定义为：二叉树或者是一个空树，或者是一个由一个根结点和两颗互不相交的分别称作根结点的左子树和右子树所组成的非空树，左子树和右子树又同样是一颗二叉树。

　

　常见基本概念：

　　1）结点的度。结点所拥有子树的个数。

　　2）叶结点

　　3）分枝结点

　　4）左孩子、右孩子、双亲

　　5）路径、路径长度

　　6）祖先、子孙

　　7）结点的层数。  规定树的根结点的层数为1，其余结点的层数 等于 它的双亲结点的层数加1。

　　8）树的深度 。树中所有结点的最大层数称为树的深度。

　　9）树的度。树中各结点度的最大值称为该树的度。叶子结点的度为0。

　　10）满二叉树。在一颗二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的一颗二叉树称作满二叉树。

　　11）完全二叉树。一颗深度为k的有n个结点的二叉树，对树中的结点按从上至下，从左至右的顺序进行编号，如果编号为i（1<=i<=n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，那么这颗二叉树被称为完全二叉树。完全二叉树的特点是：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。

　　　　需要注意的是：满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。

　　二叉树的基本性质：

　　性质1：一颗非空二叉树的第i层上最多有2^i-1个结点。（i>=1）

　　性质2：一颗深度为k的二叉树中，最多具有2^k-1个结点，最少有k个结点。

　　性质3：对于一颗非空的二叉树，度为0的结点（即叶子结点）总是比度为2的结点多一个，即叶子结点数n₀，度数为2的结点数n₂，则有n₀ = n₂+1。

　　性质4：具有n个结点的完全二叉树的深度为    向下取整(log₂ⁿ )+1。

　　性质5：如果对二叉树的根节点从0开始编号，那么相应的i号结点的双亲结点的编号为（i-1）/2，左孩子的编号为（2*i+1），右孩子的编号为（2*i+2）。

　　　　　  如果对二叉树的根节点从1开始编号，那么相应的i号结点的双亲结点的编号为 i/2 取整，左孩子的编号为（2*i），右孩子的编号为（2*i+1）。

2.如何实现二叉排序树

　　二叉排序树又称为二叉查找树，它或是一个颗空树，或者具有下列性质的二叉树：①如果左子树不空，那么左子树上所有结点的值均小于它的根结点的值；②如果右子树不空，那么右子树上所有结点的值均大于它的根结点的值；③左右子树也分别为二叉排序树。

　　比如int[]  data = {2,8,7,4,9,3,1,6,7,5},构成二叉排序树。

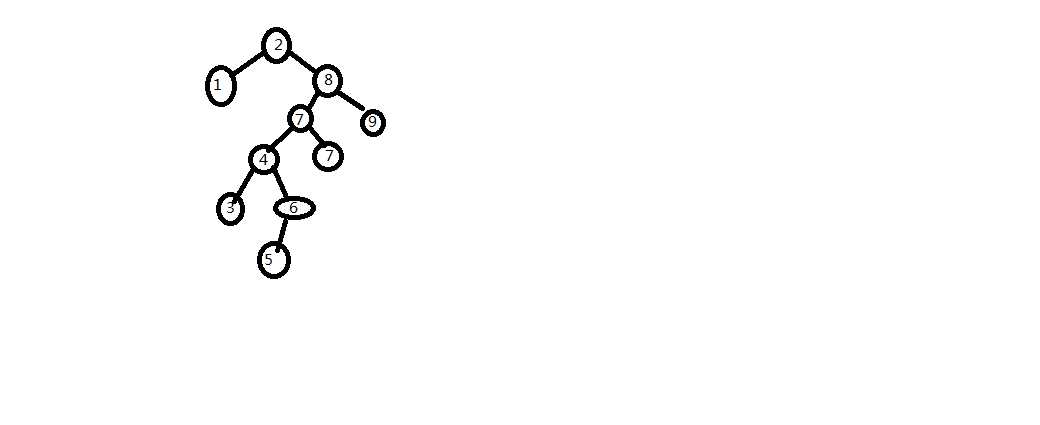
代码实现：

  1   2 
  3 import java.util.LinkedList;
  4 import java.util.Queue;
  5 
  6 /**
  7  * 二叉排序树(二叉查找数)
  8  * @author Administrator
  9  *
 10  */
 11 public class BinaryTreeSort {
 12     
 13     public Node root;
 14     public BinaryTreeSort(){
 15         root = null;
 16     }
 17     //按层遍历 二叉树  利用队列实现
 18     public void print(){
 19         if(this.root==null)
 20             return;
 21         Queue<Node> q = new LinkedList<Node>();
 22         q.add(root);
 23         while(!q.isEmpty()){
 24             Node n = q.poll();
 25             System.out.print(n.data+" ");
 26             if(n.left!=null){
 27                 q.add(n.left);
 28             }
 29             if(n.right!=null){
 30                 q.add(n.right);
 31             }
 32         }
 33     }
 34     
 35     
 36     
 37     //在二叉树中插入节点
 38     public void insert(int data){
 39         Node newNode = new Node(data);
 40         if(root == null){
 41             root = newNode;
 42             return;
 43         }
 44         Node current = root;
 45         Node parent ;
 46         while(true){
 47             parent = current;
 48             //左子树节点值小于父节点的值
 49             if(data < current.data){
 50                 current = current.left;
 51                 if(current==null){
 52                     parent.left = newNode;
 53                     return;
 54                 }
 55             }else{//右子树节点值大于父节点的值
 56                 current = current.right;
 57                 if(current == null){
 58                     parent.right = newNode;
 59                     return;
 60                 }
 61             }
 62         }
 63         
 64     }
 65     //构建二叉树
 66     public void bulidTree(int[] data){
 67         for(int i = 0;i < data.length;i++){
 68             insert(data[i]);
 69         }
 70     }
 71     //中序遍历  左中右
 72     public void inOrder(Node localRoot){
 73         if(localRoot!=null){
 74             inOrder(localRoot.left);
 75             System.out.print(localRoot.data+" ");
 76             inOrder(localRoot.right);
 77         }
 78         
 79     }
 80     public void inOrder(){
 81         this.inOrder(this.root);
 82     }
 83     //先序遍历  中左右
 84     public void preOrder(Node localRoot){
 85         if(localRoot!=null){
 86             System.out.print(localRoot.data+" ");
 87             preOrder(localRoot.left);
 88             preOrder(localRoot.right);
 89         }
 90     }
 91     public void preOrder(){
 92         this.preOrder(this.root);
 93     }
 94     //后序遍历  左右中
 95     public void postOrder(Node localRoot){
 96         if(localRoot!=null){
 97             postOrder(localRoot.left);
 98             postOrder(localRoot.right);
 99             System.out.print(localRoot.data+" ");
100         }
101     }
102     public void postOrder(){
103         this.postOrder(this.root);
104     }
105     
106     
107     public static void main(String[] args) {
108         BinaryTreeSort b = new BinaryTreeSort();
109         int[] data = {2,8,7,4,9,3,1,6,7,5};
110         b.bulidTree(data);
111         System.out.print("二叉树的中序排列:");
112         b.inOrder();
113         System.out.println();
114         System.out.print("二叉树的先序排列:");
115         b.preOrder();
116         System.out.println();
117         System.out.print("二叉树的后序排列:");
118         b.postOrder();
119         System.out.println();
120         System.out.print("二叉树按层遍历：");
121         b.print();
122     }
123 }
124 class Node{
125     public int data;
126     public Node left;
127     public Node right;
128     
129     public int leftMaxDistance;
130     public int rightMaxDistance;
131     
132     public Node(int date){
133         this.data = date;
134         this.left = null;
135         this.right = null;
136     }
137 }

 

3.如何层序遍历二叉树

　　可以使用队列实现二叉树的按层遍历。

　　主要思路：先将根结点放入队列中，然后每次从队列中取出一个结点，同时若此结点有子结点，则将它的子结点放入队列尾，直到队列为空。

 1 //按层遍历 二叉树  利用队列实现
 2     public void print(){
 3         if(this.root==null)
 4             return;
 5         Queue<Node> q = new LinkedList<Node>();
 6         q.add(root);
 7         while(!q.isEmpty()){
 8             Node n = q.poll();
 9             System.out.print(n.data+" ");
10             if(n.left!=null){
11                 q.add(n.left);
12             }
13             if(n.right!=null){
14                 q.add(n.right);
15             }
16         }
17     }

 

4.已知先序遍历和中序遍历，如何求后序遍历

二叉树的结点定义：

 1 class Node{
 2     public int data;
 3     public Node left;
 4     public Node right;
 5     
 6     public int leftMaxDistance;
 7     public int rightMaxDistance;
 8     
 9     public Node(int date){
10         this.data = date;
11         this.left = null;
12         this.right = null;
13     }
14 }

解题步骤：1.确定树的根节点

                   2.求解树的左右子树

　　　　　 3.对二叉树的左右孩子也进行1、2步，直到求出二叉树结构为止

 1 /**
 2  * 已知先序遍历和中序遍历，如何求后序遍历
 3  * @author Administrator
 4  *
 5  */
 6 public class Test1{
 7     public Node root;
 8     Test1(){
 9         this.root=null;
10     }
11     public static void main(String[] args) {
12         //同一个包内可以访问
13         Test1 b = new Test1();
14         int[] preOrder = {1,2,4,8,9,5,10,3,6,7};
15         int[] inOrder = {8,4,9,2,10,5,1,6,3,7};
16         
17         b.initTree(preOrder,inOrder);
18         System.out.print("二叉树后序遍历：");
19         b.postOrder();
20     }
21     public void postOrder(){
22         this.postOrder(this.root);
23     }
24     //后序遍历  左右中
25     public void postOrder(Node localRoot){
26         if(localRoot!=null){
27             postOrder(localRoot.left);
28             postOrder(localRoot.right);
29             System.out.print(localRoot.data+" ");
30         }
31     }
32     public void initTree(int[] preOrder, int[] inOrder){
33         root = this.initTree(preOrder,0,preOrder.length-1, inOrder,0,inOrder.length-1);
34     }
35     public Node initTree(int[] preOrder,int start1,int end1,int[] inOrder,int start2,int end2){
36         if(start1>end1 || start2>end2){
37             return null;
38         }
39         //1、根节点或者父节点
40         int rootData = preOrder[start1];
41         
42         Node head = new Node(rootData);
43         //2、找到rootData在 中序数组中的位置
44         int rootIndex = findIndexInArray(inOrder, rootData, start2, end2);
45         //3、确定 先序遍历数组中  需要的偏移量
46         int offSet = rootIndex - start2 - 1;
47         //4、构造左子树
48         Node left = initTree(preOrder, start1+1, start1+1+offSet, inOrder, start2, rootIndex-1);
49         //5、构建右子树
50         Node rgiht = initTree(preOrder, start1+offSet+2, end1, inOrder, rootIndex+1, end2);
51         
52         head.left = left;
53         head.right = rgiht;
54         //返回头结点
55         return head;
56     }
57     public int findIndexInArray(int[] inOrder,int rootData,int start2,int end2){
58         for(int i=start2 ;i <= end2 ;i++){
59             if(inOrder[i] == rootData)
60                 return i;
61         }
62         return -1;
63     }
64 }

 

5.如何求二叉树中结点的最大距离

问题描述：写一个程序求一棵二叉树中相距最远的两个结点之间的距离。

解题步骤：1.求出左子树距离根结点的最远距离

　　　　　2.求出右子树距离根结点的最远距离

　　　　　3.maxDistance = leftMaxDistance + rightMaxDistance

递归实现结点距离根结点的距离

代码实现：

 1 public class MaxDistanceBinaryTree {
 2 
 3     private static int  maxLen = 0;
 4     
 5     private static int max(int a,int b){
 6         return a>b?a:b;
 7     }
 8     
 9     public static void FindMaxDistance(Node root){
10         //如果是空二叉树，直接return
11         if(root == null)
12             return;
13         //如果左子树为空，左子树距离根节点的距离为0
14         if(root.left == null)
15             root.leftMaxDistance = 0;
16         //如果右子树为空,右子树距离根节点的距离为0
17         if(root.right == null)
18             root.rightMaxDistance = 0;
19         
20         
21         //如果根节点的左子树不为空，递归调用  根节点的左孩子
22         if(root.left != null)
23             FindMaxDistance(root.left);
24         //如果根节点的右子树不为空，递归调用  根节点的左孩子
25         if(root.right != null)
26             FindMaxDistance(root.right);
27         
28         if(root.left!=null)
29             root.leftMaxDistance = max(root.left.leftMaxDistance,root.left.rightMaxDistance)+1;
30         if(root.right!=null)
31             root.rightMaxDistance = max(root.right.leftMaxDistance,root.right.rightMaxDistance)+1;
32         
33         if(root.rightMaxDistance+root.leftMaxDistance>maxLen)
34             maxLen = root.leftMaxDistance+root.rightMaxDistance;
35     }
36     
37     public static void main(String[] args) {
38         BinaryTreeSort b = new BinaryTreeSort();//实例化一个构建二叉排序树的类
39         int[] data = {2,8,7,4,9,3,1,6,7,5};
40         b.bulidTree(data);//构建二叉排序树
41         FindMaxDistance(b.root);
42         //b.print();
43         System.out.println("maxLen :"+maxLen);
44     }
45 }