高阶函数与递归

Posted 2020-11-03 chris3201

什么是高阶函数？

　　变量可以指向函数，函数的参数能接收变量，函数可以接收另一个函数作为参数，我们称为高阶函数。

def calc(x):
    return x*x
f = calc
f = lambda x:x*x  #匿名函数

变量指向函数

x = 10
def calc(x):
    return x*x

函数接收变量

def func(x,y):
    return x + y
def calc(x):
    return x
f = calc(func)
print(f(5,6))

函数接收另一个函数当做参数

只要满足以下任意一个条件就是高阶函数：

　　1，接收一个或多个函数作为输入（参数）。

　　2，return返回另一个函数。

递归

　　递归，就是函数在运行中调用自己。

def recursion(n):
    print(n)
    recursion(n+1) #每执行一次都会调用一次自己，该函数相当于死循环
recursion(1)

递归

 出现的效果就是，这个函数在不断的调用自己，每次调用就n+1,相当于循环了。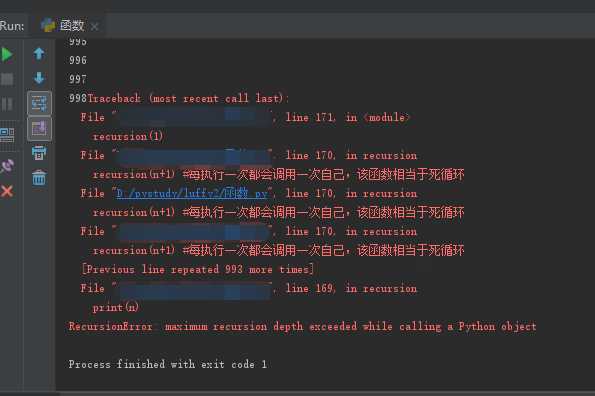

通俗来说，每个函数在调用自己的时候还没有推出，占内存多了或导致崩溃。本质是因为函数调用是通过栈（stack）这种数据结构实现的。每当进入一个函数调用栈就会加一层栈帧，每次函数返回，栈就会建一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出。

函数调用的栈结构：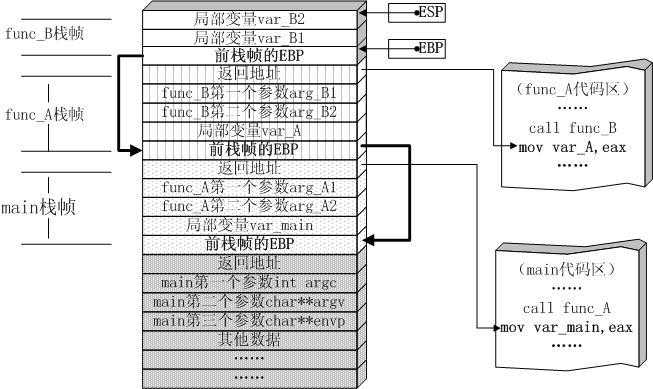

 递归的特点

让10不断除以2，直到0为止。（调用多少次，结束就也要结束多少次）

# def calc(n):
#     val = n//2
#     print(val)
#     if val ==0:
#         return 1
#     calc(val)
#     print(val) #按照反序一次一次返回
# calc(10)

def calc(n):
    print(n)
    if n //2 >0:
        calc(n//2)
    print(n)
calc(10)

10除以2递归

 求阶乘

任何大于1的自然数n阶乘表示方法：
n!=1*2*3*4*5*6*...*n  或者 n!=n*(n-1)!
即举例：4!=4*3*2*1=24

def factorial(n):
    if n ==1:
        return 1
    return n*factorial(n-1)
print(factorial(5))

===> factorial(5)
===> 5 * factorial(4)
===> 5 * (4 * factorial(3))
===> 5 * (4 * (3 * factorial(2)))
===> 5 * (4 * (3 * (2 * factorial(1))))
===> 5 * (4 * (3 * (2 * 1)))
===> 5 * (4 * (3 * 2))
===> 5 * (4 * 6)
===> 5 * 24
===> 120

阶层

递归：a,自己调用自己。b,有结束条件   两个必须满足

尾递归是指，在函数返回的时候，调用自身本身，并且，return语句不能包含表达式。这样，编译器或者解释器就可以把尾递归做优化，使递归本身无论调用多少次，都只占用一个栈帧，不会出现栈溢出的情况。

def fact(n):
    return fact_iter(n, 1)

def fact_iter(num, product):
    if num == 1:
        return product
    return fact_iter(num - 1, num * product)
print(fact(5))
print(fact_iter(5,1))

可以看到，return fact_iter(num - 1, num * product)仅返回递归函数本身，num - 1和num * product在函数调用前就会被计算，不影响函数调用。

fact(5)对应的fact_iter(5, 1)的调用如下：

===> fact_iter(5, 1)
===> fact_iter(4, 5)
===> fact_iter(3, 20)
===> fact_iter(2, 60)
===> fact_iter(1, 120)
===> 120
尾递归调用时，如果做了优化，栈不会增长，因此，无论多少次调用也不会导致栈溢出。

小结

使用递归函数的优点是逻辑简单清晰，缺点是过深的调用会导致栈溢出。

针对尾递归优化的语言可以通过尾递归防止栈溢出。尾递归事实上和循环是等价的，没有循环语句的编程语言只能通过尾递归实现循环。

Python标准的解释器没有针对尾递归做优化，任何递归函数都存在栈溢出的问题。