1.学习总结(2分)
1.1树结构思维导图
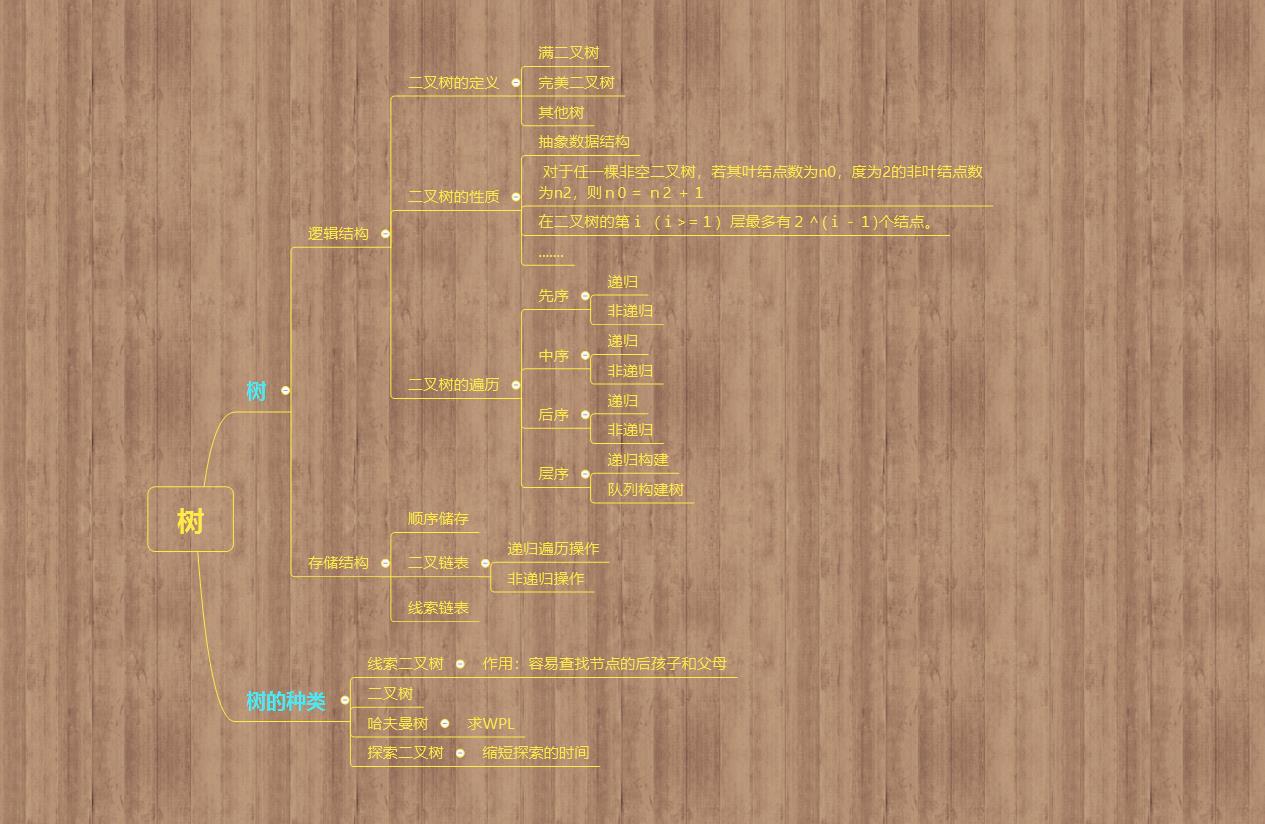
1.2 树结构学习体会
1.递归进行树的操作和递归树的构建不是弄得很清楚,难度大
2.PTA的题目比较难,尤其6-4通过递归求后缀表达式的值真的难理解,很多题目都操作起来比较复杂.
3.通过先序和中序以及通过后序和中序来确立树的递归操作不是很好理解
4.对树的操作不是很清楚,基本全是看课本
2.PTA实验作业
2.1 题目1:6-4 jmu-ds-表达式树
2.2 设计思路
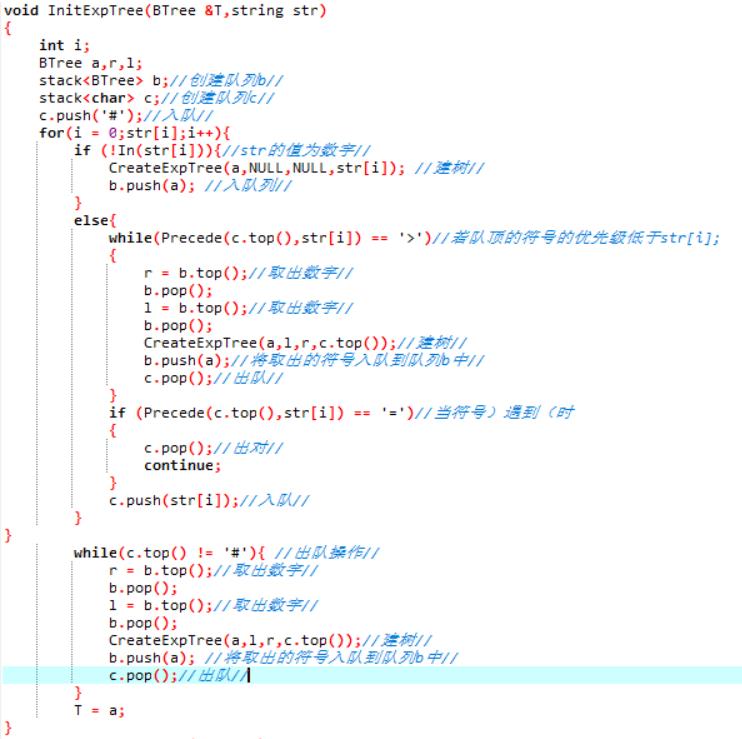
1.BTree a,r.l建树
2.stack<char> c,stack<char> c建队列 c.push(\'#\').
3.for i=0 to str[i] 表达式的建树
4.str[i]为数字,b.push(a);
5.while Precede(c.top(),str[i]) == \'>\',CreateExpTree(a,l,r,c.top());
6.if 当符号)遇到(时 出队
7.c.push(str[i]);
8.while c.top() != \'#\' 建树操作
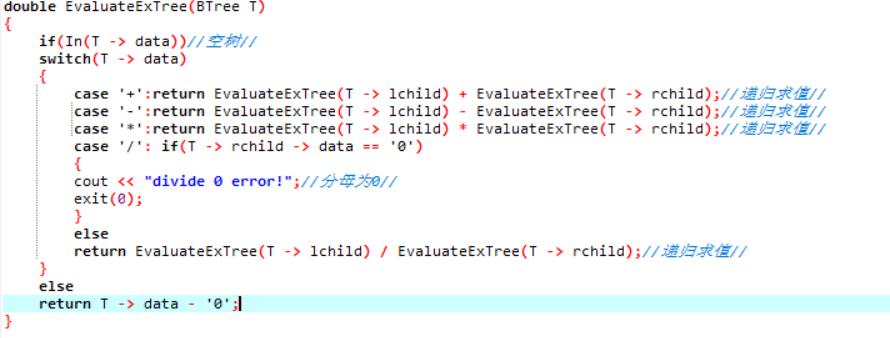
9.EvaluateExTree(T -> lchild) ?EvaluateExTree(T -> rchild);递归求值.
2.3 代码截图
2.4 PTA提交列表说明

建树的错误操作造成段错误
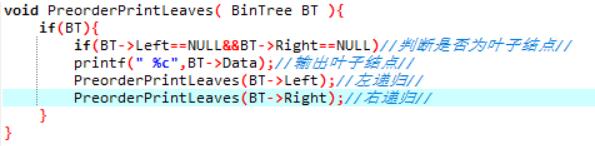
2.1 题目2:6-3 先序输出叶结点
2.2 设计思路
1.判断叶子结点 BT->Left==NULL&&BT->Right==NULL
2.PreorderPrintLeaves(BT->Left);左递归
3.PreorderPrintLeaves(BT->Right);右递归
2.3 代码截图
2.4 PTA提交列表说明

输出叶结点的类型为字符型
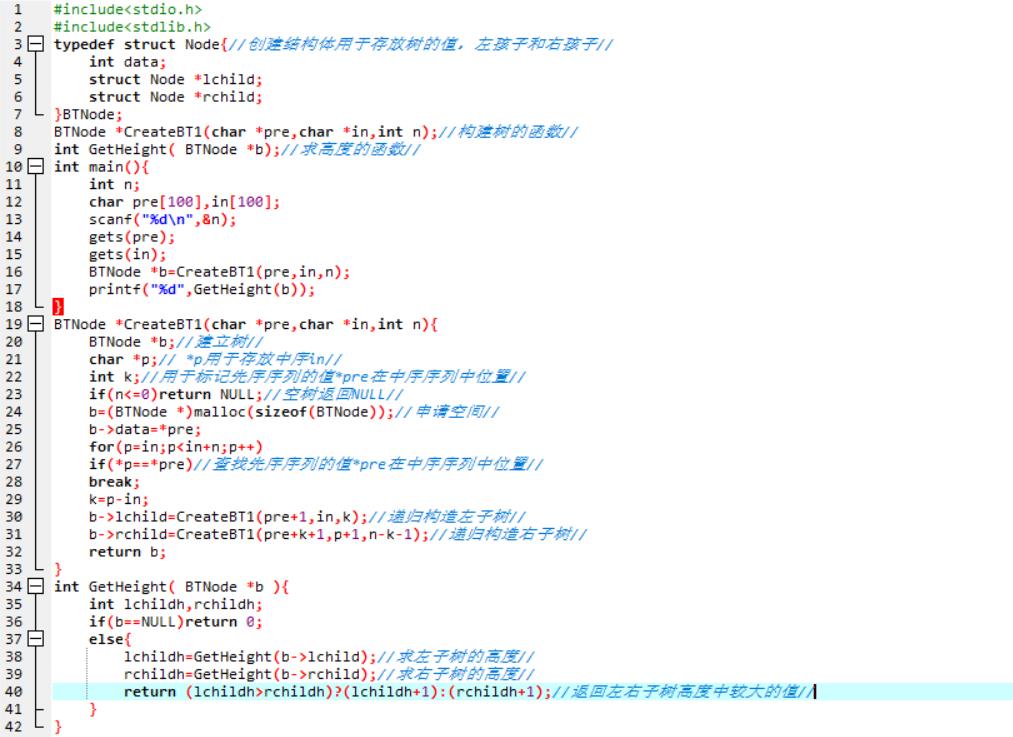
2.1 题目3:7-1 还原二叉树
2.2 设计思路
1.创建树的结构体用于存放树的值,左孩子和右孩子
2.构建树的函数CreateBT1(pre,in,n).
3.建树b,*p存放中序in,k用于标记先序序列的值*pre在中序序列中位置
4.n<=0 return NULL;
5.b申请空间,b->data=*pre;。
6.for p=in to in+n 在中序中查找*pre所在的位置k.
7.递归构造左右子树.
8.递归求左右子树的高度,return Max.
2.3 代码截图
2.4 PTA提交列表说明

3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的得分:
我的得分:180分
4. 阅读代码
愿天下有情人都是失散多年的兄妹
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int fa[10005]={0},mo[10005]={0},sex[10005],visit[10005]={0},flag;
void dfs(int a,int n){
if(n==0) return;
if(visit[a]==1){
flag=1;
return;
}
visit[a]=1;
// cout<<a<<" ";
if(fa[a]!=-1 && fa[a]!=0) dfs(fa[a],n-1);
if(mo[a]!=-1 && mo[a]!=0) dfs(mo[a],n-1);
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
int num;
cin>>num;
char c;
cin>>c;
if(c==\'M\') sex[num]=0;
else sex[num]=1;
int f,m;
cin>>f>>m;
fa[num]=f,mo[num]=m;
sex[f]=0; sex[m]=1;
}
int k;
cin>>k;
for(int i=0;i<k;i++){
int a,b;
cin>>a>>b;
memset(visit,0,sizeof(visit));
if(sex[a]==sex[b]){
cout<<"Never Mind"<<endl;
continue;
}
flag=0;
dfs(a,5);
dfs(b,4);
if(flag==0) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}