1.学习总结
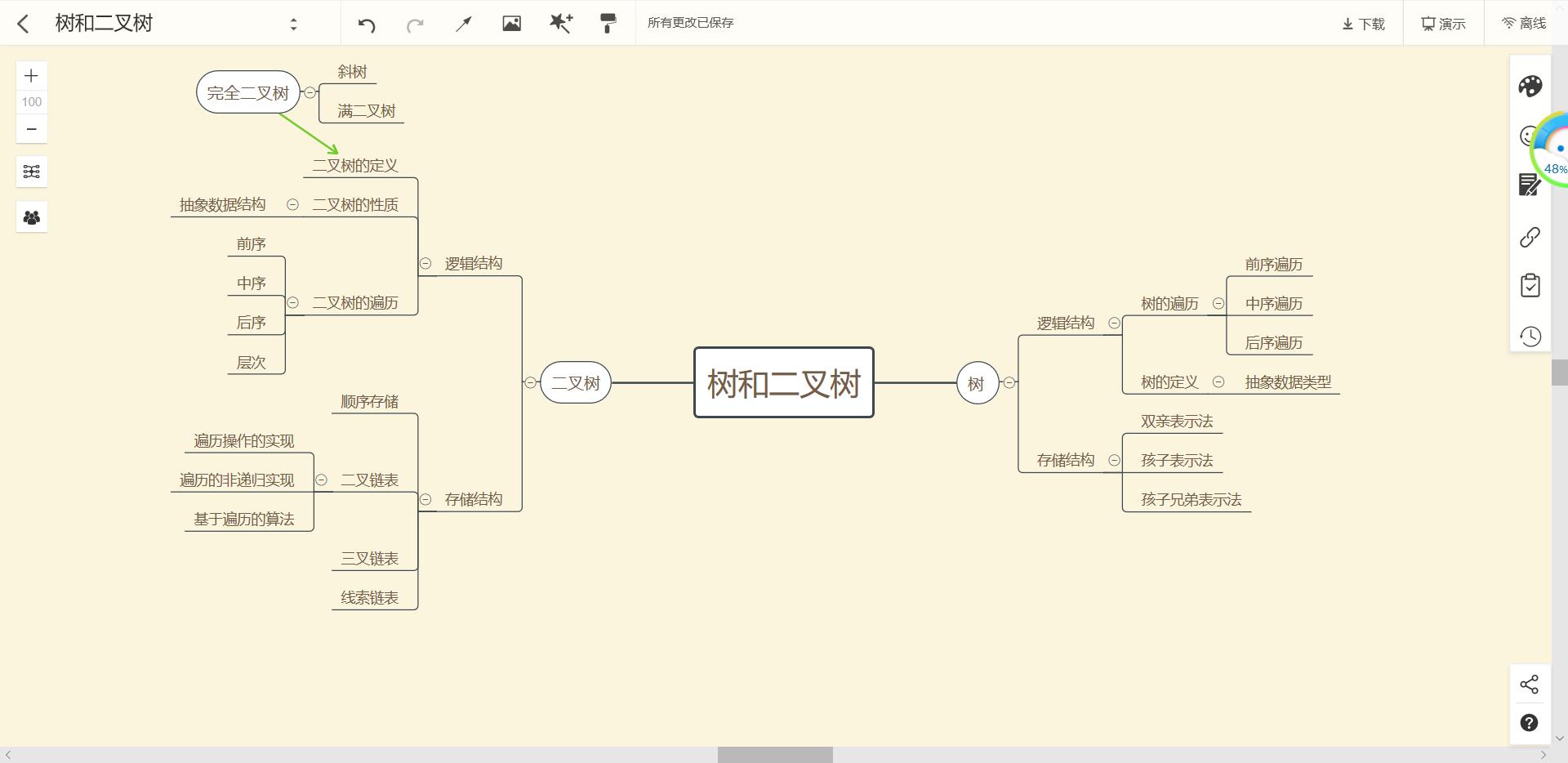
1.1树结构思维导图
1.2 树结构学习体会
认识:
树(tree)是包含n(n>0)个结点的有穷集,其中:
(1)每个元素称为结点(node);
(2)有一个特定的结点被称为根结点或树根(root)。
(3)除根结点之外的其余数据元素被分为m(m≥0)个互不相交的集合T1,T2,……Tm-1,其中每一个集合Ti(1<=i<=m)本身也是一棵树,被称作原树的子树(subtree)。
困难:
学习树的过程中,二叉树方面我理解的相对比较多,对于线索树那方面的知识点还是模糊的,前序,中序,后序遍历也基本掌握了,其他知识希望在以后的学习中慢慢巩固。
2.PTA实验作业
题目1:6-2 求二叉树高度
设计思路
int GetHeight( BinTree BT )
{
定义整型变量m,n,a分储存左子树与右子树的高度
若树为空 则返回0
递归调用本函数
m=GetHeight(BT->Left);
n=GetHeight(BT->Right);
取两者中较大者为a
返回a+1
}
代码截图
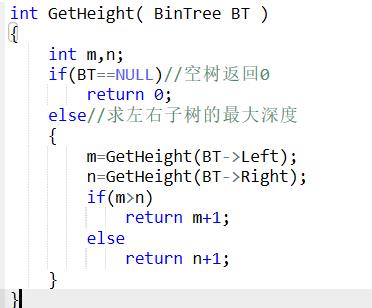
PTA提交列表说明

第一次提交是由于if语句判定条件没考虑全面而导致的只有空树时正确,将m,n中较大者赋值给a后再返回a+1则不会出现此类问题后两次编译错误是在修改的的时候没加函数头导致的。
题目2:7-2 根据后序和中序遍历输出先序遍历
设计思路
void houzhong(int h[],int z[],int size)
{
如果树为空则返回0;
定义temp并使,定义一个数组xian[ ]来储存先序遍历 定义整型变量k=0用来遍历xian[]数组
temp=后序最后一个节点 为先序的根节点
xian[k++] = temp
while{
找到根节点在中序中的位置
}
运用递归调用
houzhong(h,z,index);
houzhong(h+index,z+index+1,size-index-1);
直至每次递归调用的后序,中序遍历数组为空;
}
代码截图
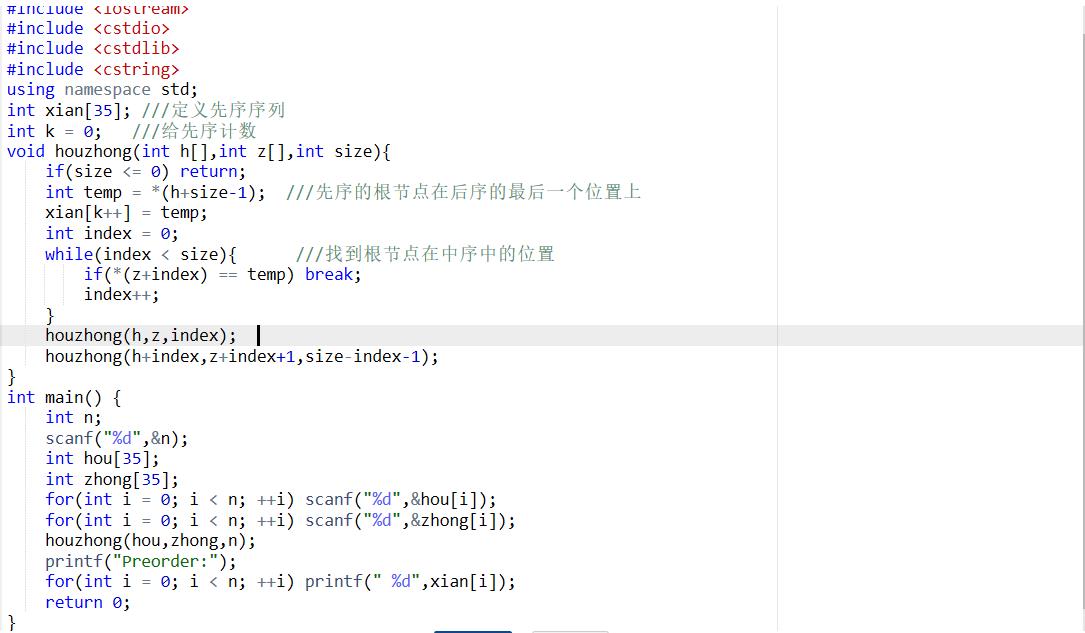
PTA提交列表说明

这一题由于我对递归调用运用不太好也可以说是比较笨想不出怎么用递归 是通过网上找代码跟问同学做出来的,所以没经过多少修改,贴出来练习是因为想熟悉递归操作。
题目3:6-4 jmu-ds-表达式树
设计思路
void InitExpTree(BTree &T,string str){
建树形栈用来储存数字
符号型栈来储存符号
‘#’入符号栈
while 字符串不为空
if 字符不是运算符 建新节点T
赋值并将左右孩子为空
T入栈s
else
若栈op顶部的字符大于字符串第i个字符
建立新的节点T且栈顶元素赋值给T
T入栈s 指向op栈顶
若等于
访问栈顶 i++
若小于
进栈 i++
while op栈顶元素不为‘#’
建立新节点并将op栈顶元素辅助
右孩子为s栈顶元素
if s栈顶不为空
左孩子为栈顶元素并再次访问栈顶
T入栈s
访问op栈顶
}
代码截图
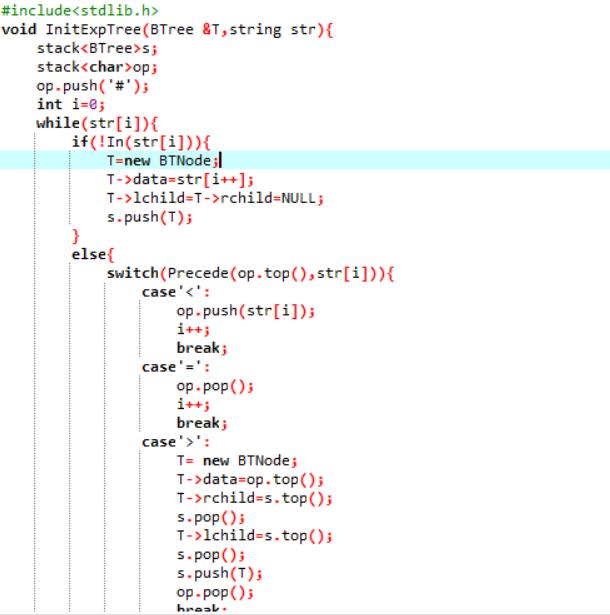
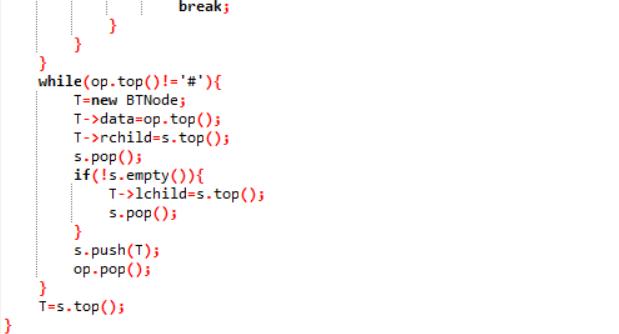
PTA提交列表说明

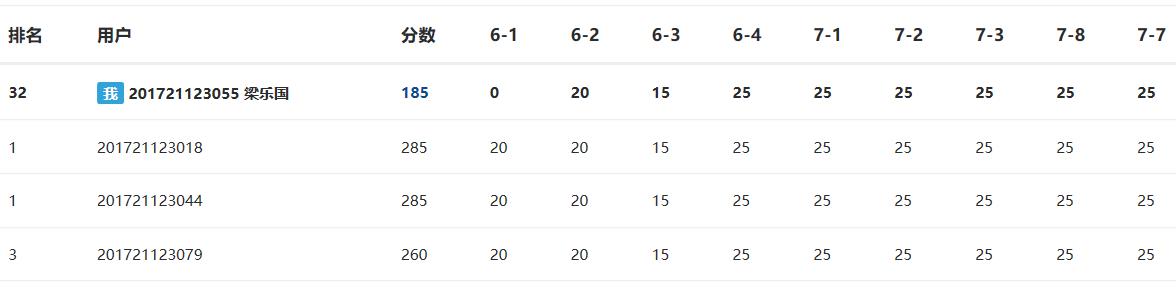
3.截图本周题目集的PTA最后排名
4. 阅读代码
代码1:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct BiTNode{
char e;
struct BiTNode *lchild,*rchild;
}BiTNode;
void preOrderTravse(BiTNode *T1){
if(T1){
printf("%c",T1->e);
preOrderTravse(T1->lchild);
preOrderTravse(T1->rchild);
}
}
void inOrderTravse(BiTNode *T1){
if(T1){
inOrderTravse(T1->lchild);
printf("%c",T1->e);
inOrderTravse(T1->rchild);
}
}
void postOrderTravse(BiTNode *T1){
if(T1){
postOrderTravse(T1->lchild);
postOrderTravse(T1->rchild);
printf("%c",T1->e);
}
}
int CreateBiTree(BiTNode **T1,char *preString,char *inString,int start,int end){
if(start==end){
*T1=NULL;
}
else{
*T1=(BiTNode*)malloc(sizeof(BiTNode));
int middle=start;
while(inString[middle]!=*preString) middle++;
(*T1)->e=*preString;
preString++;
CreateBiTree(&((*T1)->lchild),preString,inString,start,middle);
preString+=middle-start; //特别注意这一点:不是加middle,而是加middle-start!
CreateBiTree(&((*T1)->rchild),preString,inString,middle+1,end);
}
return 1;
}
int main(){
/*
char preString[]="ABECDFGHIJ",inString[]="EBCDAFHIGJ";
*/
//更通用的方法:
char *preString,*inString;
char pre[50],in[50];
preString=pre;
inString=in;
printf("请输入前序序列:");
gets(preString);
printf("请输入中序序列:");
gets(inString);
//
int start=0,end=0;
end=strlen(preString); //start、end是指当前inString串的起始与结束
BiTNode *T1;
CreateBiTree(&T1,preString,inString,start,end);
preOrderTravse(T1);
printf("\\n");
inOrderTravse(T1);
printf("\\n");
postOrderTravse(T1);
return 0;
}
代码2:
ypedef char ElemType;
typedef struct btnode //二叉树的结点定义
{
ElemType data;
btnode *leftchild;
btnode *rightchild;
}BtNode,*BtTree;
//在中序序列中查找元素函数
int find (char *is,char ch)
{
if (is == NULL)
{
exit (1);
}
int i = 0;
while (is[i] != 0)
{
if (is[i] == ch)
{
return i;
}
else
{
i ++;
}
}
return -1;
}
BtNode *NiceCreatTreePI (char *ps,char *is)
{
if (NULL == ps && NULL == is)
{
return NULL;
}
int isindex[MAXSIZE] = {0}; //用数组模拟一个顺序栈 (从数组最后入栈和出栈)
for (int j = 0;j < MAXSIZE;j ++) //初始化全用-1表示,以便出栈处理
{
isindex[j] = -1;
}
int i = 0;
SeqStack s;
Init_stack (&s);
BtNode * p = BuyNode ();
p -> data = *ps;
Push (&s,p);
BtNode *child = NULL;
BtNode *tree = p;
int index1 = find (is,*ps);
isindex[i ++] = index1; //相当于进栈
int index2 = index1;
while (*(ps + 1) != 0)
{
index1 = index2;
index2 = find (is,*(ps + 1));
if (index1 == -1 || index2 == -1)
{
exit (1);
}
if (index1 > index2) //左子树
{
child = BuyNode ();
ps ++;
child -> data = *ps;
p -> leftchild = child;
p = p -> leftchild;
Push (&s,child);
isindex[i ++] = index2;
}
else //右子树
{
i --;
while (i >= 0 && index2 > isindex[i])
{
p = top (&s);
pop (&s);
isindex[i] = -1;
i --;
}
child = BuyNode ();
ps ++;
child -> data = *ps;
p -> rightchild = child;
p = p -> rightchild;
Push (&s,child);
i ++;
isindex[i ++] = index2;
}
}
return tree;
}
功能:代码1和2分别是给出二叉树先序与中序序列分别以递归和非递归的算法来构建二叉树,因为本次上机考对于构建二叉树的代码不是太熟练,所以贴出来希望能掌握。