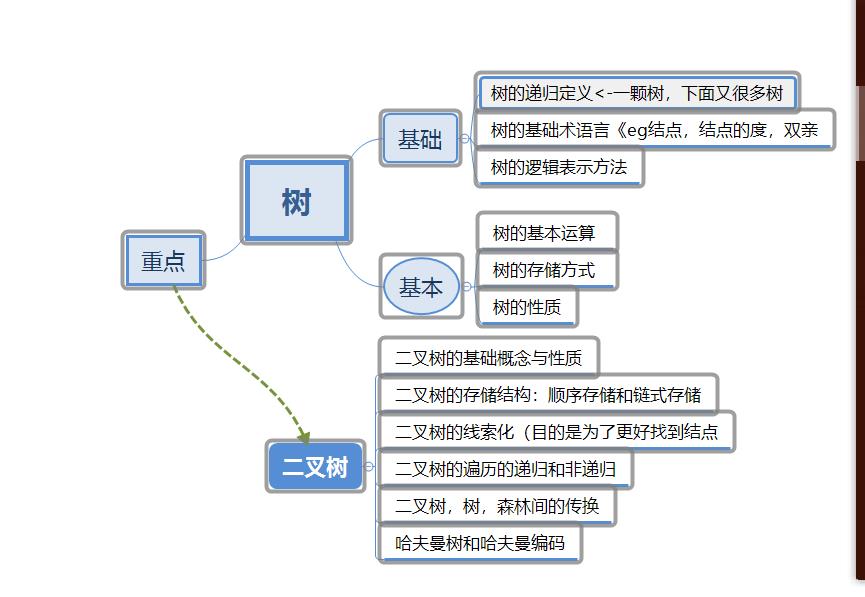
第四次作业 树

Posted 2020-11-02 .sugar

 

 

 

 

1.2 树结构学习体会

难，不是我等凡夫俗子可以学会的。

困难点：对递归的理解不够透彻，一直转不过来。

解决办法：多看点代码。

2.PTA实验作业

题目一:6-4 jmu-ds-表达式树（25 分）

题目：

• 输入一行中缀表达式，转换一颗二叉表达式树，并求解.
• 表达式只包含+，-，*，/，（，）运算符，操作数只有一位，且为整数(有兴趣同学可以考虑负数小数，两位数做法)。按照先括号，再乘除，后加减的规则构造二叉树。
• 如图所示是"1+(2+3)*2-4/5"代数表达式对应二叉树，用对应的二叉树计算表达式的值。 转换二叉树如下：

思路：

建立表达式二叉树

定义栈 s 用来存储用运算的数字

定义字符栈 o p 用来存储数字运算符号

首先 将’#‘ 如栈op

当str不为空的时候 进行while

if 是数字

 就建立一个树节点，将它赋值为str{i}的值，还要就左右孩子弄成NULL,  还要入栈

else 调动Precede

对它出现的运算符一一进行运作，

用swich

while  op的top不是#

创建新的树节点

赋予为op.top的值

在将栈里的后面两个值分别给左右孩子

/*计算表达式树*/

利用递归把所有字符转换成数字

while 若有树节点

就计算

 

 

 

 

 

 

 4.PTA提交列表说明

题目二:6-1 jmu-ds-二叉树操作集（20 分）

本题要求用层次法创建二叉树，层次法输入序列是按树的从上到下从左到右的顺序形成，各层的空节点用字符 #表示

2.设计思路：

根据层次字符序列创建二叉树

定义一个队列q；

一个树 temp

if str是#

就直接ruturn

else 建立一个树节点

左右孩子为NULL；

将str【i】赋值给它

就节点入队列

while ！队列

出队列

分别判断字符串后两个是否为空

不是空：建立新节点，赋值

 

 

 

 

 

 

 

 

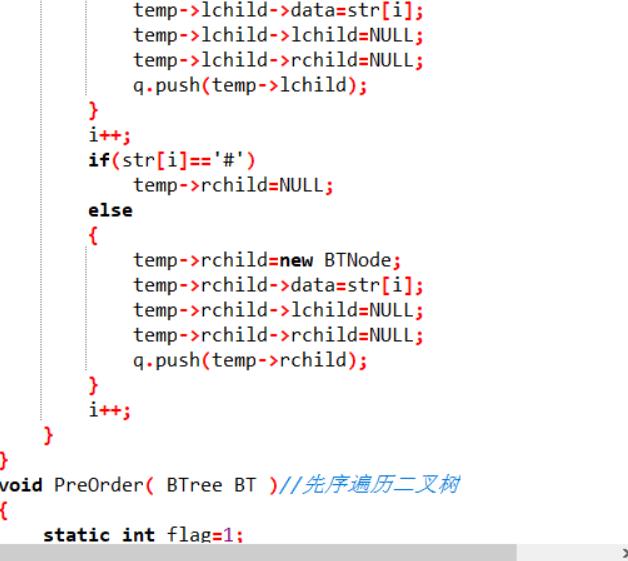
6-3 先序输出叶结点（15 分）

本题要求按照先序遍历的顺序输出给定二叉树的叶结点。

2.设计思路：

if ！BT 结束

当左右孩子多NULL时

就输出节点

 

 

总分

 185

也就是2分

4.阅读代码

1. //huffmanCoding.c  
2. #include <stdio.h>  
3. #include <limits.h>  
4. #include <string.h>  
5. #include <stdlib.h>  
6. #define N 6  
7.   
8. typedef struct huffNode  
9. {  
10.     unsigned int weight;   //权重  
11.     unsigned int lchild,rchild,parent;  //左右子节点和父节点  
12. }HTNode,*HuffTree;  
13. typedef char **HuffCode;  
14.   
15. //找出数组中无父节点且权值最小的两个节点下标,分别用s1和s2保存  
16. void select(const HuffTree &HT,int n,int &s1,int &s2);  
17. //HT:哈夫曼树，HC:哈夫曼编码，w:构造哈夫曼树节点的权值，n:构造哈夫曼树节点的个数  
18. void HuffmanCode(HuffTree &HT,HuffCode &HC,int *w,int n);  
19.   
20.   
21. int main()  
22. {  
23.     int i;  
24.     char key[N] = {\'0\',\'A\',\'B\',\'C\',\'D\',\'E\'};//第0个元素保留不用  
25.     int w[N] = {0,1,2,4,5,6}; //第0个元素保留不用  
26.     HuffTree HT;  
27.     HuffCode HC;  
28.     HuffmanCode(HT,HC,w,N - 1);  
29.     for ( i = 1; i < N; i++ )  
30.     printf("%c:%s\\n",key[i],HC[i]);    
31.     
32.     printf("\\n");      
33.     return 0;  
34. }  
35.   
36.   
37.   
38.   
39. //找出数组中权值最小的两个节点下标,分别用s1和s2保存  
40. void select(const HuffTree &HT,int n,int &s1,int &s2)  
41. {  
42.     int i;  
43.     s1 = s2 = 0;   
44.     int min1 = INT_MAX;//最小值，INT_MAX在<limits.h>中定义的  
45.     int min2 = INT_MAX;//次小值  
46.   
47.     for ( i = 1; i <= n; ++i )  
48.     {  
49.     if ( HT[i].parent == 0 )  
50.     {//筛选没有父节点的最小和次小权值下标  
51.         if ( HT[i].weight < min1 )  
52.         {//如果比最小值小  
53.         min2 = min1;  
54.         s2 = s1;  
55.         min1 = HT[i].weight;  
56.         s1 = i;  
57.         }  
58.         else if ( (HT[i].weight >= min1) && (HT[i].weight < min2) )  
59.         {//如果大于等于最小值，且小于次小值  
60.         min2 = HT[i].weight;  
61.         s2 = i;  
62.         }  
63.         else  
64.         {//如果大于次小值，则什么都不做  
65.         ;  
66.         }  
67.     }  
68.     }  
69. }  
70.   
71. //HT:哈夫曼树，HC:哈夫曼编码，w:构造哈夫曼树节点的权值，n:构造哈夫曼树节点的个数  
72. void HuffmanCode(HuffTree &HT,HuffCode &HC,int *w,int n)  
73. {  
74.     int s1;  
75.     int s2;  
76.     int m = 2 * n - 1;       //容易知道n个节点构造的哈夫曼树是2n-1个节点  
77.     int i,c,f,j;  
78.     char *code;  //暂存编码的  
79.     HT = (HuffTree)malloc((m+1)*sizeof(HTNode));  //0单元未使用  
80.       
81.   
82.     for ( i = 1; i <= n; i++ )  
83.         HT[i] = {w[i],0,0,0};//初始化前n个节点(构造哈夫曼树的原始节点)  
84.       
85.     for ( i = n + 1; i <= m; i++ )  
86.     HT[i] = {0,0,0,0};  //初始化后n-1个节点  
87.   
88.     //构建哈夫曼树  
89.     for ( i = n + 1; i <= m; i++)  
90.     {  
91.     select(HT,i-1,s1,s2);//找出前i-1个节点中权值最小的节点下标  
92.     HT[s1].parent = i;  
93.     HT[s2].parent = i;  
94.     HT[i].lchild = s1;  
95.     HT[i].rchild = s2;  
96.     HT[i].weight = HT[s1].weight + HT[s2].weight;  
97.     }  
98.     //哈夫曼编码  
99.     HC = (char **)malloc((n)*sizeof(char *));  
100.     //暂存编码  
101.     code = (char *)malloc(n*sizeof(char));//使用了第0单元  
102.     for ( i = 1; i <= n; i++ )  
103.     {  
104.     for ( c = i, f = HT[c].parent, j = 0; f != 0; c = HT[c].parent, f = HT[c].parent,  j++ )  
105.     {//从叶子扫描到根  
106.         if ( HT[f].lchild == c )   
107.         {  
108.         code[j] = \'0\';  
109.         }  
110.         else if(HT[f].rchild == c)  
111.         {  
112.         code[j] = \'1\';  
113.         }  
114.         else  
115.         {//否则什么也不做  
116.         ;  
117.         }  
118.     }  
119.     code[j] = \'\\0\';  
120.     HC[i] = (char *)malloc(strlen(code)*sizeof(char));  
121.     strcpy(HC[i],code);  
122.     }  
123.       
124. }