第04次作业-树

Posted 2020-11-02 阙广壬辰

1.学习总结

1.1树结构思维导图

1.2 树结构学习体会

树的结构：非线性结构，也是递归型的结构，属于集合之间的关系。

困难：如果对递归的算法不是很领悟的时候，对树的一些操作的问题还是不容易理解。

树结构可以解决的问题：

并查集问题

家谱处理问题

 哈夫曼编码的问题

表达式转换的问题

2.PTA实验作业

2.1 题目1

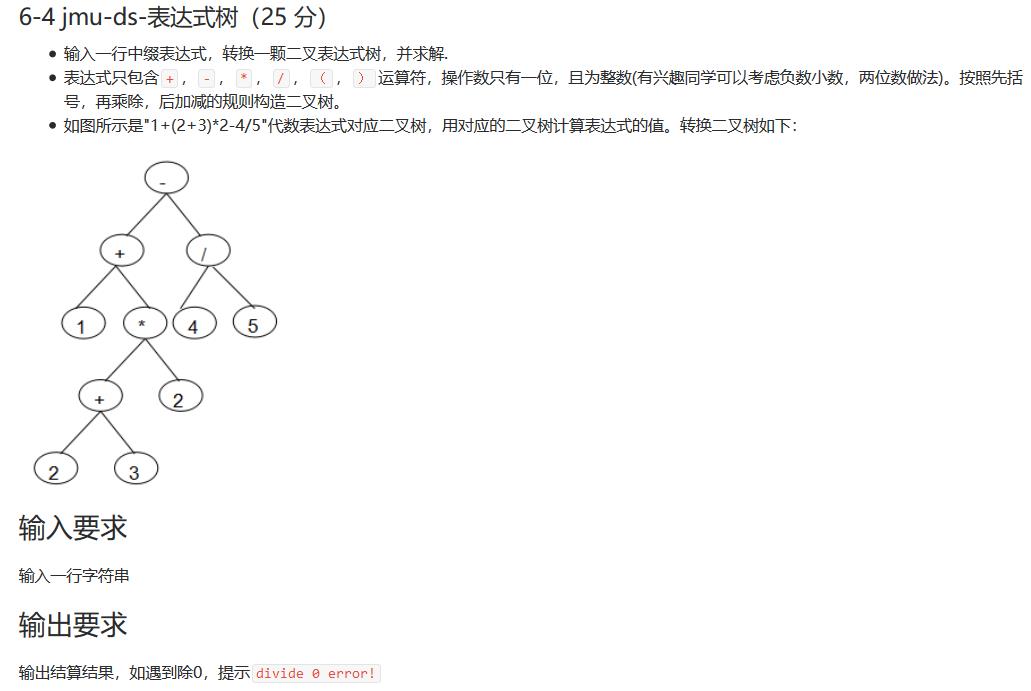
2.2设计思路

void InitExpTree(BTree &T,string str)  //建表达式的二叉树
{
	stack<BTree>s;
  	stack<char>op;
  	将#进op栈
	while 表达式未结束 
	{	if str 不为运算符
			将后续的数字存到s栈中
		else
			switch(Precede(op栈顶运算符，str)) 
			{	case \'<\' 栈顶运算符优先级低 
					op.push(str)
					从str中读取下一个字符
					break;
				case \'=\'
					只有两个括号满足这个情况
					从str读取下一个字符
					break;
				case \'>\' 栈s运算符执行
				 	建立结点  
					s.push( );
					break; 
			} 
	} 
	while op顶不为 \'#\'
		从s中取两个结点
　　　　　　　　　 s.push( );
		break; 
}

 2.3代码截图

 

2.4 PTA提交列表说明。

这题在老师没讲之前，我是想利用栈将中缀表达式转换成后缀表达式在建树，但是后面发现这是道函数题，不能再自己写一个函数了

然后在老师的讲解之下发现可以直接利用中缀表达式建树，那所有问题迎刃而解了。只有清楚< = >三种情况下时候的操作建树就没问题了。

2.1 题目2

 

2.2设计思路

集合大概存储方式：

 存储方式就是如此

void match
{
	int child,parent;
	输入表达关系的一句话
	让child为第一个人物的下标
	让parent为第二个人物的下标
	switch(关系)
	{
		case parent ：判断父母 
		case child ：判断父母反过来
		case sibling ：判断兄弟 
		case ancestor ：判断祖先 
		case descendant ：判断祖先反过来 
	}
	if 正确 输出true
	else false 
}
int Trace(int child)
{
//	从该名字往前找到第一个空格比他少的名字就是他的parent；
	for i=child-1 to 0
		if 空格少 return i;
	return -1;
}
bool CheckParent(int child,int parent)
{
	if Trace(child)==parent  true
	else false
}
bool CheckAncestor(int child,int ancetor)
{
	while c!=-1
		if CheckParent(c,an) true;
		else c = Trace(c);
	false;
}
bool CheckSibling(int child1,int child2)
{
	if Trace(child1)==Trace(child2) true;
	else false;
}

 2.3代码截图

2.4 PTA提交列表说明。

这题的注意事项：

1.只有同一个parent的才能叫sibling；
2.从该名字往前找到第一个空格比他少的名字就是他的parent；
3.Ancestor必须是parent的parent的……parent，而不仅仅是空格比他少就行。

4.此题输入较多，在输入方面会造成缓存区未清空的现象（空格没被吃掉），导致输入未匹配上，这要注意

 

2.1 题目3

选择这题的原因：这题是用到了哈夫曼树的思想，但是并没有去建树，而是用到了优先队列，我想粗略了解下优先队列

 优先队列：priority_queue

头文件：#include<queue>

定义：priority_queue<类型名>队列名

priority_queue<int> q;   　　　　　　　　　　　　  //定义元素从大到小的出队的队列q

priority_queue<int,vector<int>, greater<int> > q;  　　//定义元素从小到大的出队的队列q

 

和普通queue操作不同的是，他没有back和front，反而只有top

 
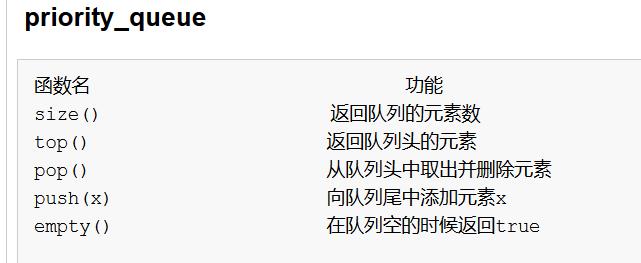
欲了解更多优先队列知识可参考

点我获取更多知识

 

2.2设计思路

priority_queue<int,vector<int>,greater<int> >Q;
初始化小先出队列的优先队列
cin -> n
for i=0 to n-1
	cin -> m
	Q.push(m)
while (Q is not empty){
	Q.pop()->x
	if(Q is not empty)
	{
		Q.pop()->y
		sum=sum+x+y
		产生新的结点Q.push()->(x+y) 
	}
}
cout -> sum

2.3代码截图

 

2.4 PTA提交列表说明。

额。。。注意切换编译器吧。

3.1 PTA排名截图

3.2 我的总分：3分

4. 阅读代码

二叉树及其遍历 树的同构

　　戳我观看

这道题目的精髓之处在于十分考验对建树，遍历，递归的理解。

建树的时候是用到了顺序存储

在判断是否同构的函数里面，凭借分析各种情况去return,有利于加深新手对树的递归模型的理解。

5. 代码Git提交记录截图