[从头学数学] 第217节 带着计算机去高考

Posted 2020-07-10 mwsister

剧情提要：
[机器小伟]在[工程师阿伟]的陪同下进入了[九转金丹]之第八转的修炼。设想一个场景：
如果允许你带一台不连网的计算机去参加高考，你会放弃选择一个手拿计算器和草稿本吗
？阿伟决定和小伟来尝试一下用计算机算高考题会是怎样的感觉。

正剧开始：

星历2016年05月23日 12:04:40, 银河系厄尔斯星球中华帝国江南行省。
[工程师阿伟]正在和[机器小伟]一起做着2008年的江苏省数学高考题]。

从2005年开始，[人叫板老师]发布了新的修炼功法，就是[机器小伟]

一直以来参照修炼的那部。

然后三年过去了，这一年，所有的修士们都将在全新的模式下进行试炼。

这是新型试炼的第一年。

所以说这个试炼的总分应该是720分，对吧。

所以，根据上面的信息来看，选理科的修士，从此将面对一张总分是200分的数学卷子了。

这张卷子是这样的：

选择题从此说再见了，剩下了14个填空题，主观题重新回到了六个，另外再加四个附加题。

这次的难度不高也不低，考虑到没有选择题可以蒙分，再加上附加题要占用时间，

所以阿伟给评为5环难度。

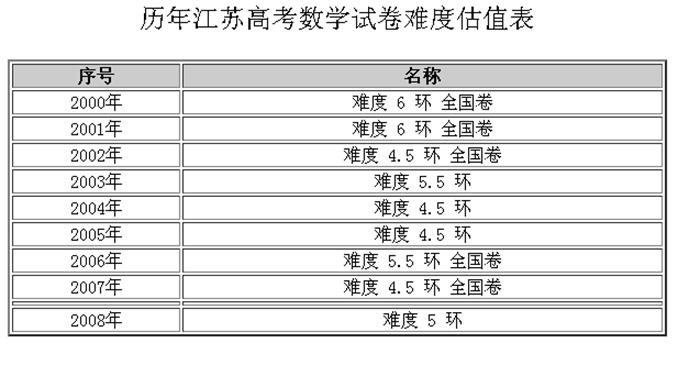
这张卷子里关于不等式这一块的知识考察那是满天飞啊，足足占据了半壁江山。

<span style="font-size:18px;">#题3
>>> (1+1j)/(1-1j);
1j
</span>

<span style="font-size:18px;">#题4
###
# @usage   多项式运算相关
# @author  mw
# @date    2016年05月23日  星期一  09:36:12 
# @param
# @return
#
###
class Polynomial():
    #格式化打印
    def printPoly(self, array, variable = 'x'):
        len_ = len(array);
        poly = [];
        
        for i in range(len_):
            if (i < len_ -1):
                s = '('+str(array[i])+')*'+variable+'^['+str(len_-1-i)+']';
            else:
                s = '('+str(array[i])+')';
            poly.append(s);

        s = '';
        for i in range(len_):
            s += poly[i];
            if (i < len_ - 1):
                s += '+';
        
        print(s); #格式：(1)*x^[3]+(2)*x^[2]+(-3)*x^[1]+(4)
        return poly;
            
    #解不等式
    def inequality(self, array, symbol = '<'):
        #方程的根
        roots = np.roots(array);
        roots = sorted(roots);
        #print(roots);
        len_ = len(roots);

        p = np.poly1d(array);
        #符合要求的区间
        section = [];

        if (symbol == '<'):
            if (p(roots[0]-1) < 0):
                section.append(['-inf', roots[0]]);
            if (p(roots[len_-1]+1))< 0:
                section.append([roots[len_-1], 'inf']);
        elif (symbol == '>'):
            if (p(roots[0]-1)) > 0:
                section.append(['-inf', roots[0]]);
            if (p(roots[len_-1]+1)) > 0:
                section.append([roots[len_-1], 'inf']);
            
        for i in range(len_-1):
            mid = (roots[i]+roots[i+1])/2;
            if (symbol == '<'):
                if p(mid) < 0:
                    section.append([roots[i], roots[i+1]]);
            elif (symbol == '>'):
                if p(mid) > 0:
                    section.append([roots[i], roots[i+1]]);  
        return section;
    

def tmp4():
    poly = Polynomial();

    #根据两个根求得多项式
    a = np.poly1d([1, 1], True);
    a = np.array(a);
    poly.printPoly(a, 'x');

    #根据多项式系数得多项式
    b = [-3, -7];
    b = np.array(b);

    #两个多项式相加
    c = np.polyadd(a, b);
    poly.printPoly(c, 'x');

    #求根
    d = poly.inequality(c, '<');
    print(d);</span>

<span style="font-size:18px;">   #计算代数式的值
    #代数式具有[(coef)*expr^[exp], ...]这种形式
    #要加载自制的alg模块
    def algValue(self, stralg, valueTable):
        #多项式的项数
        len_s = len(stralg);
        #参数对照表的项数
        #参数对照表具有[['x', '1'], ['y', '3']]这样的形式
        len_v = len(valueTable);

        for i in range(len_s):
            s = stralg[i];

            for j in range(len_v):
                s = s.replace(valueTable[j][0], str(valueTable[j][1]));

            s = s.replace('^[', '**(');
            s = s.replace(']', ')');

            stralg[i] = eval(s);

        return stralg;     

def tmp5():
    poly = Polynomial();

    a = alg.strformat(['5a', '-b']);
    a = alg.strpow_n(a, 2);
    a = alg.strcombine(a); #['(25)*a^[2]', '(-10)*a^[1]*b^[1]', '(1)*b^[2]']
    #print(a);

    #代数式中各代号的值
    value = [['a', 1], ['b', 3]];

    b = poly.algValue(a, value); #['(25)*1**(2)', '(-10)*1**(1)*3**(1)', '(1)*3**(2)'] [25, -30, 9]
    #print(b);

    c = np.dot(b, [1, -0.5, 1]); #49.0
    print(c);
    print(c**0.5);</span>

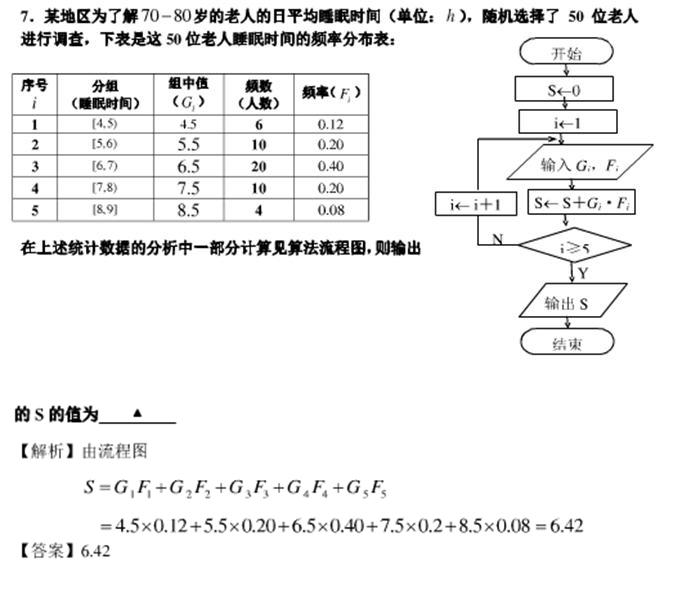
这就是新出的算法题，引入了程序的框架图，虽然不难，却很好玩。

<span style="font-size:18px;">#题7
def tmp7():
    G = [4.5, 5.5, 6.5, 7.5, 8.5];
    F = [0.12, 0.20, 0.40, 0.20, 0.08];

    s = 0;
    
    for i in range(1, 6):
        s += G[i-1]*F[i-1];

    print(s);
	
>>> 
6.42</span>

上面是填空题部分，基本都是三、四环的难度，运算量一般。

<span style="font-size:18px;">#题15
def tmp15():
    A = np.arccos(2**0.5/10);
    B = np.arccos(2*5**0.5/5);

    print(np.tan(A+B));
    print((A+2*B)*180/np.pi);
	
>>> 
-3.0
135.0
</span>

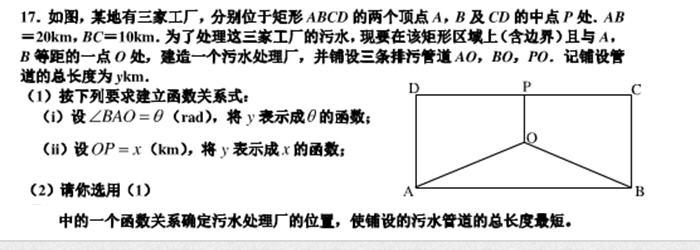
下面就是第一次亮相登场的附加题了，本来以为会很难，但仔细一看，

都是3环到4环的难度。但这些题难度虽然不大，但总归要占时间的。

这也就是为什么这张普遍难度在4环的卷子可以评到5环难度。

因为要做14个填空再加10个解答。

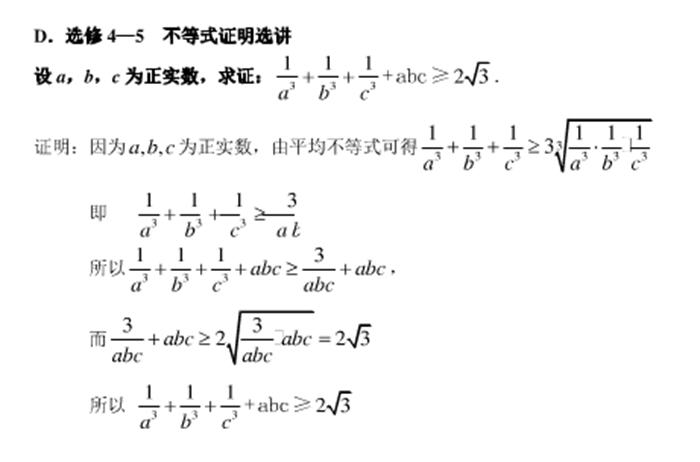
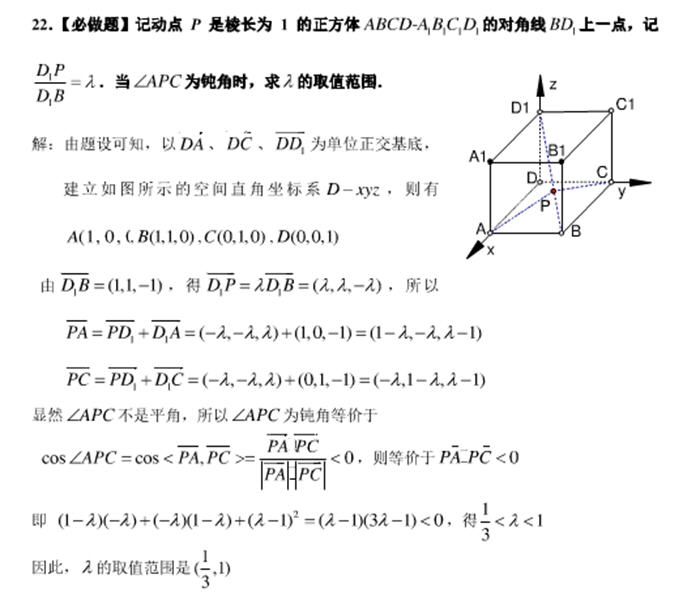
整理一下工具：

<span style="font-size:18px;">###
# @usage   多项式运算相关
# @author  mw
# @date    2016年05月23日  星期一  09:36:12 
# @param
# @return
#
###
class Polynomial():
    #格式化打印
    def printPoly(self, array, variable = 'x'):
        len_ = len(array);
        poly = [];
        
        for i in range(len_):
            if (i < len_ -1):
                s = '('+str(array[i])+')*'+variable+'^['+str(len_-1-i)+']';
            else:
                s = '('+str(array[i])+')';
            poly.append(s);

        s = '';
        for i in range(len_):
            s += poly[i];
            if (i < len_ - 1):
                s += '+';
        
        print(s); #格式：(1)*x^[3]+(2)*x^[2]+(-3)*x^[1]+(4)
        return poly;
            
    #解不等式
    def inequality(self, array, symbol = '<'):
        #方程的根
        roots = np.roots(array);
        roots = sorted(roots);
        #print(roots);
        len_ = len(roots);

        p = np.poly1d(array);
        #符合要求的区间
        section = [];

        if (symbol == '<'):
            if (p(roots[0]-1) < 0):
                section.append(['-inf', roots[0]]);
            if (p(roots[len_-1]+1))< 0:
                section.append([roots[len_-1], 'inf']);
        elif (symbol == '>'):
            if (p(roots[0]-1)) > 0:
                section.append(['-inf', roots[0]]);
            if (p(roots[len_-1]+1)) > 0:
                section.append([roots[len_-1], 'inf']);
            
        for i in range(len_-1):
            mid = (roots[i]+roots[i+1])/2;
            if (symbol == '<'):
                if p(mid) < 0:
                    section.append([roots[i], roots[i+1]]);
            elif (symbol == '>'):
                if p(mid) > 0:
                    section.append([roots[i], roots[i+1]]);  
        return section;

    #计算代数式的值
    #代数式具有[(coef)*expr^[exp], ...]这种形式
    #要加载自制的alg模块
    def algValue(self, stralg, valueTable):
        #多项式的项数
        len_s = len(stralg);
        #参数对照表的项数
        #参数对照表具有[['x', '1'], ['y', '3']]这样的形式
        len_v = len(valueTable);

        for i in range(len_s):
            s = stralg[i];

            for j in range(len_v):
                s = s.replace(valueTable[j][0], str(valueTable[j][1]));

            s = s.replace('^[', '**(');
            s = s.replace(']', ')');

            stralg[i] = eval(s);

        return stralg;</span>

本节到此结束，欲知后事如何，请看下回分解。