拓扑排序

Posted 2020-11-02 Akmpfen

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了拓扑排序相关的知识，希望对你有一定的参考价值。

拓扑排序

有向无环图（DAG）

例1：https://hihocoder.com/problemset/problem/1174

#1174 : 拓扑排序·一

描述

由于今天上课的老师讲的特别无聊，小Hi和小Ho偷偷地聊了起来。

小Ho：小Hi，你这学期有选什么课么？

小Hi：挺多的，比如XXX1,XXX2还有XXX3。本来想选YYY2的，但是好像没有先选过YYY1，不能选YYY2。

小Ho：先修课程真是个麻烦的东西呢。

小Hi：没错呢。好多课程都有先修课程，每次选课之前都得先查查有没有先修。教务公布的先修课程记录都是好多年前的，不但有重复的信息，好像很多都不正确了。

小Ho：课程太多了，教务也没法整理吧。他们也没法一个一个确认有没有写错。

小Hi：这不正是轮到小Ho你出马的时候了么！

小Ho：哎？？

我们都知道大学的课程是可以自己选择的，每一个学期可以自由选择打算学习的课程。唯一限制我们选课是一些课程之间的顺序关系：有的难度很大的课程可能会有一些前置课程的要求。比如课程A是课程B的前置课程，则要求先学习完A课程，才可以选择B课程。大学的教务收集了所有课程的顺序关系，但由于系统故障，可能有一些信息出现了错误。现在小Ho把信息都告诉你，请你帮小Ho判断一下这些信息是否有误。错误的信息主要是指出现了"课程A是课程B的前置课程，同时课程B也是课程A的前置课程"这样的情况。当然"课程A是课程B的前置课程，课程B是课程C的前置课程，课程C是课程A的前置课程"这类也是错误的。

提示：拓扑排序

输入

第1行：1个整数T，表示数据的组数T(1 <= T <= 5)
接下来T组数据按照以下格式：
第1行：2个整数，N,M。N表示课程总数量，课程编号为1..N。M表示顺序关系的数量。1 <= N <= 100,000. 1 <= M <= 500,000
第2..M+1行：每行2个整数，A,B。表示课程A是课程B的前置课程。

输出

第1..T行：每行1个字符串，若该组信息无误，输出"Correct"，若该组信息有误，输出"Wrong"。

样例输入

样例输出　　Wrong

　　　　　　Correct

思路：拓扑模板题；

#include <iostream>
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=1000005;
int n,m;
vector <int> G[maxn];
int inedge[maxn];   //记录每个点的入度；
bool topsort()
{
    queue<int> que;
    int cnt=0;
    for(int i=1;i<=n;i++)if(!inedge[i])que.push(i);     //选出入度为0的点;
    while(!que.empty())
    {
        int now=que.front();
        que.pop();
        cnt++;              //记录入度为0的点的总数;
        for(int i=0;i<G[now].size();i++){
            if(--inedge[G[now][i]]==0)que.push(G[now][i]);//遍历相邻结点，删边;
        }
    }
    if(cnt==n)return true;  //所有点均入度为0过;
    return false;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int a,b;
        memset(inedge,0,sizeof(inedge));
        for(int i=0;i<=n;i++)   //这里不清空WA了一回0.0
            G[i].clear();
        scanf("%d%d",&n,&m);
        for(int i=0;i<m;i++)
        {
            scanf("%d%d",&a,&b);
            G[a].push_back(b);  //记录每个点相邻的出度的点；
            inedge[b]++;
        }
        if(topsort())
            cout << "Correct" << endl;
        else
            cout << "Wrong" <<endl;
    }
    return 0;
}

例2：https://hihocoder.com/problemset/problem/1175

#1175 : 拓扑排序·二

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Hi和小Ho所在学校的校园网被黑客入侵并投放了病毒。这事在校内BBS上立刻引起了大家的讨论，当然小Hi和小Ho也参与到了其中。从大家各自了解的情况中，小Hi和小Ho整理得到了以下的信息：

校园网主干是由N个节点(编号1..N)组成，这些节点之间有一些单向的网路连接。若存在一条网路连接(u,v)链接了节点u和节点v，则节点u可以向节点v发送信息，但是节点v不能通过该链接向节点u发送信息。
在刚感染病毒时，校园网立刻切断了一些网络链接，恰好使得剩下网络连接不存在环，避免了节点被反复感染。也就是说从节点i扩散出的病毒，一定不会再回到节点i。
当1个病毒感染了节点后，它并不会检查这个节点是否被感染，而是直接将自身的拷贝向所有邻居节点发送，它自身则会留在当前节点。所以一个节点有可能存在多个病毒。
现在已经知道黑客在一开始在K个节点上分别投放了一个病毒。

举个例子，假设切断部分网络连接后学校网络如下图所示，由4个节点和4条链接构成。最开始只有节点1上有病毒。

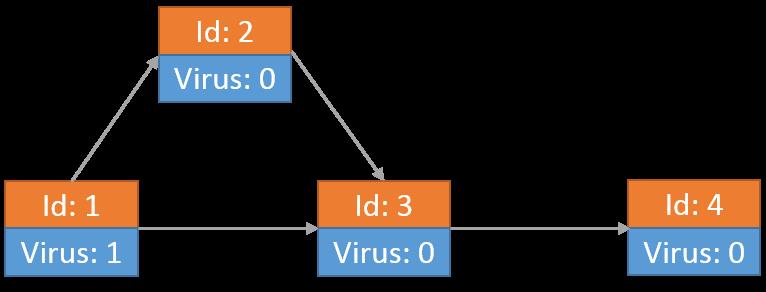
最开始节点1向节点2和节点3传送了病毒，自身留有1个病毒：

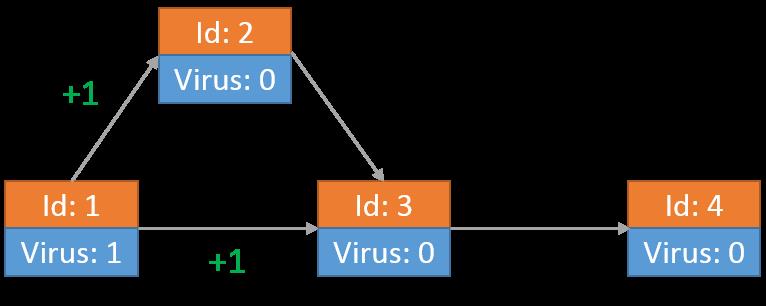
其中一个病毒到达节点2后，向节点3传送了一个病毒。另一个到达节点3的病毒向节点4发送自己的拷贝：

当从节点2传送到节点3的病毒到达之后，该病毒又发送了一份自己的拷贝向节点4。此时节点3上留有2个病毒：

最后每个节点上的病毒为：

小Hi和小Ho根据目前的情况发现一段时间之后，所有的节点病毒数量一定不会再发生变化。那么对于整个网络来说，最后会有多少个病毒呢？

提示：拓扑排序的应用

输入

第1行：3个整数N,M,K，1≤K≤N≤100,000，1≤M≤500,000

第2行：K个整数A[i]，A[i]表示黑客在节点A[i]上放了1个病毒。1≤A[i]≤N

第3..M+2行：每行2个整数 u,v，表示存在一条从节点u到节点v的网络链接。数据保证为无环图。1≤u,v≤N

输出

第1行：1个整数，表示最后整个网络的病毒数量 MOD 142857

样例输入

样例输出　　6

思路：简单拓扑走一遍，注意中间运算值别爆就行；

#include <iostream>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>

using namespace std;
const int maxn=1000005;
const int mod=142857;
int n,m,k,N[maxn],ans=0,inedge[maxn];
vector<int> G[maxn];
void topsort()
{
    ans=0;
    queue<int> que;
    for(int i=1;i<=n;i++)   //寻找初始入度为0的点;
        if(!inedge[i])que.push(i);
    while(!que.empty())
    {
        int now=que.front();
        que.pop();
        ans=(ans+N[now])%mod;
        for(int i=0;i<G[now].size();i++)
        {
            if(--inedge[G[now][i]]==0)que.push(G[now][i]);
            N[G[now][i]]=(N[G[now][i]]+N[now])%mod; //这里没取模WA了一次0.0;
        }
    }
}
int main()
{
    while(~scanf("%d%d%d",&n,&m,&k))
    {
        int a,b;
        memset(N,0,sizeof(N));
        memset(inedge,0,sizeof(inedge));
        for(int i=0;i<=n;i++)
            G[i].clear();
        for(int i=0;i<k;i++)
        {
            scanf("%d",&a);
            N[a]=1;
        }
        for(int i=0;i<m;i++)
        {
            scanf("%d%d",&a,&b);
            G[a].push_back(b);
            inedge[b]++;
        }
        topsort();
        printf("%d\\n",ans);
    }
    return 0;
}

例3：https://nanti.jisuanke.com/t/16957

In this winter holiday, Bob has a plan for skiing at the mountain resort.

This ski resort has

The $S_iSi-th flag to the T_iTi-th flag has length L_iLi.$

Each path must follow the principal of reduction of heights and the start point must be higher than the end point strictly.

An available ski trail would start from a flag, passing through several flags along the paths, and end at another flag.

Now, you should help Bob find the longest available ski trail in the ski resort.

Input Format

The first line contains an integer

In each test case, the first line contains two integers $\\leq 100000<N≤10000 and 0 < M \\leq 1000000<M≤100000as described above.$

Each of the following $S_iSi, T_iTi, and L_i~(0 < L_i < 1000)Li (0<Li<1000) describing a path in the ski resort.$

Output Format

For each test case, ouput one integer representing the length of the longest ski trail.

样例输入

样例输出

题目来源

2017 ACM-ICPC 亚洲区（乌鲁木齐赛区）网络赛

思路：从上往下滑雪就是有向无环图，用数组记录滑到每个点的长度，最后遍历取最长就行；

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>

using namespace std;
const int maxn=10005;
typedef long long ll;
typedef pair<int,int> p;
int n,m,inedge[maxn],dp[maxn];
vector<p> G[maxn];
void topsort()
{
    queue<int> que;
    for(int i=1;i<=n;i++)
        if(!inedge[i])que.push(i);
    while(!que.empty())
    {
        int now=que.front();
        que.pop();
        for(int i=0;i<G[now].size();i++)
        {
            if(--inedge[G[now][i].first]==0)que.push(G[now][i].first);
            dp[G[now][i].first]=max(dp[G[now][i].first],dp[now]+G[now][i].second);
        }
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int a,b,c,ans=-1;
        memset(inedge,0,sizeof(inedge));
        memset(dp,0,sizeof(dp));
        for(int i=0;i<n;i++)
            G[i].clear();
        scanf("%d%d",&n,&m);
        for(int i=0;i<m;i++)
        {
            scanf("%d%d%d",&a,&b,&c);
            G[a].push_back(p(b,c));
            inedge[b]++;
        }
        topsort();
        for(int i=1;i<=n;i++)
            ans=max(ans,dp[i]);
        printf("%d\\n",ans);
    }
    return 0;
}

例4：http://codeforces.com/contest/915/problem/D

You are given a directed graph consisting of n vertices and m edges (each edge is directed, so it can be traversed in only one direction). You are allowed to remove at most one edge from it.

Can you make this graph acyclic by removing at most one edge from it? A directed graph is called acyclic iff it doesn\'t contain any cycle (a non-empty path that starts and ends in the same vertex).

Input

The first line contains two integers n and m (2 ≤ n ≤ 500, 1 ≤ m ≤ min(n(n - 1), 100000)) — the number of vertices and the number of edges, respectively.

Then m lines follow. Each line contains two integers u and v denoting a directed edge going from vertex u to vertex v (1 ≤ u, v ≤ n, u ≠ v). Each ordered pair (u, v) is listed at most once (there is at most one directed edge from u to v).

Output

If it is possible to make this graph acyclic by removing at most one edge, print YES. Otherwise, print NO.

Examples

input

Copy

output

Copy

YES

input

Copy

output

Copy

NO

Note

In the first example you can remove edge $\text{[math]}$ , and the graph becomes acyclic.

In the second example you have to remove at least two edges (for example, $\text{[math]}$ and $\text{[math]}$ ) in order to make the graph acyclic.

思路：暴力对每一个入度大于等于1的点，进行拓扑排序；

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
const int maxn=504;
int n,m,inedge[maxn],ruedge[maxn];
vector<int> G[maxn];

bool topsort()
{
    int cnt=0;
    queue<int> que;
    for(int i=1;i<=n;i++)
        if(!inedge[i])que.push(i);
    while(!que.empty())
    {
        int now=que.front();
        que.pop();
        cnt++;
        for(int i=0;i<G[now].size();i++)
            if(--inedge[G[now][i]]==0)que.push(G[now][i]);
    }
    if(cnt==n)return true;
    else return false;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        G[u].push_back(v);
        inedge[v]++;
        ruedge[v]++;
    }
    if(topsort())
        cout << "YES" << endl;
    else
    {
        for(int i=1;i<=n;i++)
        {
            memcpy(inedge,ruedge,sizeof(ruedge));
            if(inedge[i]>=1);
            inedge[i]--;
            if(topsort()){
                cout << "YES" << endl;
                return 0;
            }
        }
        cout << "NO" << endl;
    }
    return 0;
}

以上是关于拓扑排序的主要内容，如果未能解决你的问题，请参考以下文章

拓扑排序代码：

使用 C# 代码实现拓扑排序

UVA10305 拓扑排序

【数据结构】请写出以下AOV网的拓扑排序序列

数据结构问题~啥图可以进行拓扑排序~啥图不能进行拓扑排序？

拓扑排序之变量序列代码