二叉查找树

Posted 2020-11-02 凄夜

　　二叉树的定义是一棵树的每个节点最多只有两个儿子，使二叉树成为二叉查找树的性质是，对于树中的每个节点X，它的左子树中的关键字比X中的小，而它的右子树则比X中的关键字大。

　　二叉树节点可以定义成如下形式：

1 struct BSTreeNode {
2     BSTreeNode* pLeft;
3     BSTreeNode* pRight;
4     int nData;
5 };

　　二叉树非常简单，下面再介绍几个基本的操作。

　　一、插入

　　　　插入一个关键字Key从根节点开始，如果Key比此节点关键字大，则往右边继续往下，直到节点为空，以下代码为非递归写法，要写成递归写法也是非常容易的

 1 //返回树的根节点
 2 BSTreeNode* BSTreeInsert(BSTreeNode* pRoot, int nData) {
 3     if (pRoot == nullptr) {
 4         pRoot = new BSTreeNode;
 5         pRoot->pLeft = pRoot->pRight = nullptr;
 6         pRoot->nData = nData;
 7     }
 8     else {
 9         BSTreeNode* pParent = pRoot;
10         BSTreeNode* pCursor = pParent;
11         while (pCursor) {
12             pParent = pCursor;
13             if (nData > pCursor->nData)
14                 pCursor = pCursor->pRight;
15             else if (nData < pCursor->nData)
16                 pCursor = pCursor->pLeft;
17             else
18                 return pRoot;
19         }
20         pCursor = new BSTreeNode;
21         pCursor->nData = nData;
22         pCursor->pLeft = pCursor->pRight = nullptr;
23         if (nData > pParent->nData)
24             pParent->pRight = pCursor;
25         else if (nData < pParent->nData)
26             pParent->pLeft = pCursor;
27     }
28     return pRoot;
29 }

　　二、获取最小值

　　　　一直往左边遍历，直到节点为空。

 1 BSTreeNode* BSTreeMinimumNode(BSTreeNode* pRoot) {
 2     if (pRoot == nullptr)
 3         return nullptr;
 4 
 5     BSTreeNode* pCursor = pRoot;
 6     while (pCursor->pLeft) {
 7         pCursor = pCursor->pLeft;
 8     }
 9     return pCursor;
10 }

　　三、获取最大值

　　　　一直往右边遍历，直到节点为空。

 1 BSTreeNode* BSTreeMaximumNode(BSTreeNode* pRoot) {
 2     if (pRoot == nullptr)
 3         return nullptr;
 4 
 5     BSTreeNode* pCursor = pRoot;
 6     while (pCursor->pRight) {
 7         pCursor = pCursor->pRight;
 8     }
 9     return pCursor;
10 }

　　四、删除

　　　　二叉查找树的删除稍复杂一些，先查找此树待删除节点，当找到此节点（设为X）时，先判断左子节点和右子节点是否为空，如果有任一子节点为空，则删除非常容易，只需要将空节点的兄弟节点代替要删除的节点   　　即可。而如果左子节点和右子节点都不为空，则在待删除节点的右子树中找一个值最小的节点（设为Y），然后将此最小节点的值赋值给待删除结点X，然后在右子树中删除此最小节点Y，而且Y必定左子节点为空的，删除会非常简单。代码如下：

 1 BSTreeNode* BSTreeDelete(BSTreeNode* pRoot, int nData) {
 2     if (pRoot == nullptr)
 3         return nullptr;
 4     else if (nData > pRoot->nData) {
 5         pRoot->pRight = BSTreeDelete(pRoot->pRight, nData);
 6         return pRoot;
 7     }
 8     else if (nData < pRoot->nData) {
 9         pRoot->pLeft = BSTreeDelete(pRoot->pLeft, nData);
10         return pRoot;
11     }
12     else {
13         if (pRoot->pLeft == nullptr || pRoot->pRight == nullptr) {
14             BSTreeNode* pNode = (pRoot->pRight == nullptr) ? pRoot->pLeft : pRoot->pRight;
15             delete pRoot;
16             return pNode;
17         }
18         else {
19             BSTreeNode* pNode = BSTreeMinimumNode(pRoot->pRight);
20             pRoot->nData = pNode->nData;
21             pRoot->pRight = BSTreeDelete(pRoot->pRight, pNode->nData);
22             return pRoot;
23         }
24     }
25 }

　　返回值是传入的树被删除nData后树的根节点。删除后，通过递归回溯，将返回值赋值给原节点对应的左子树或右子树。

　　在《算法导论》里面，采用的是非递归删除，所以在那里讨论如果X的左右子节点不为空，则查找右子树中的后继节点Y（也就是最小节点）时，还讨论了如果后继Y是X的右子节点的情况，如果是右子节点则直接拿Y替换X，否则拿Y的右子节点先替换X中的值，再拿Y的右子节点替换Y。个人感觉不如递归删除的代码简洁明了。而且非递归删除里面，节点必须保持对父节点的引用，也就是说节点的定义里面要加一个父节点指针。

　　五、二叉树的遍历

　　　　二叉树的遍历有三种遍历方式，先序遍历，中序遍历，后序遍历

　　　　先序遍历：本身，左子节点，右子节点。

　　　　中序遍历：左子节点，本身，右子节点。

　　　　后序遍历：左子节点，右子节点，本身。

　　以以下二叉树为例：

　　　　　　

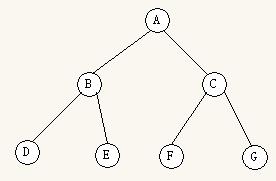
　　先序遍历输出：ABDECFG

　　中序遍历输出：DBEAFCG

　　后序遍历输出：DEBFGCA

　　由以上可知，中序遍历输出的是排序好的结果。

　　六、查找

　　　　查找就不用说了，二叉查找树，在平均情况下，时间为O(logN),也就是树的高度