[2018大华软件创新挑战赛]模拟赛第四题
Posted NULL
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[2018大华软件创新挑战赛]模拟赛第四题相关的知识,希望对你有一定的参考价值。
| 题目 | 输入 | 输出 | 限制 | 示例 |
|
node_buffer定义了一个用于存储int型数据的缓冲器,请实现其声明的所有成员方法,并满足如下要求: |
输入的第一行指定用例数量T; |
node_buffer中剩余的节点数据值,使用空格隔开; | K > 0 |
class node_buffer { public: Input: Output: |
|
网络上有一台流媒体服务器S和一台客户端C,S向C发送流媒体数据。 1、S的发送速率为M; 请设计一个函数handle_data_func,用来处理缓冲区B,并计算C第一次向S发送重启发送数据命令的时间T0及每次发送重启命令的的时间间隔T1。 |
输入的第一行指定用例数量T; |
客户端C第一次向服务端S发送重启发送数据命令的时间及时间间隔。 | 不考虑网络上的延时。 |
int handle_data_func(int M,int N,int X,int &T1) |
| 有一种特殊的正整数(int类型),将数分为两侧,每侧至少有一位数,两侧的每个数字相加相等,请写出判断的方法用来检测是否这种数。
比如:1236,可以拆分为123和6。 |
输入的第一行指定用例数量T; |
输出是否为特殊的正整数 | bool is_magicnum(int number)
intput: output: |
|
|
某股票操盘手账户里有N支股票,股价互不等,分别为v1,v2...vn;每支股票的持有股数为m1,m2...mn。现在操盘手要回笼资金需要卖出股票,假设卖出价格即为当前股价,请问能回笼多少种不同的资金量。比如:两支股票,股价分别为10、11,数量为1、2,则能回笼0、10、11、22、21、32,总共6种资金量 |
输入的第一行指定用例数量T; |
输出不同资金量的个数 |
1<=n<=10 |
Input: Output: |
第一题:

1 #include "iostream"
2 #include "algorithm"
3 #include "vector"
4
5 using namespace std;
6
7 class node_buffer
8 {
9 public:
10 // 构造函数
11 // 参数: max_size 指定缓冲的最大节点数
12 node_buffer(int max_size)
13 {
14 m_queue = (int*)malloc(sizeof(int)*max_size);
15 m_max_size = max_size;
16 m_front = 0;
17 m_size = 0;
18 m_back = -1;
19 }
20
21 // 析构函数
22 ~node_buffer()
23 {
24 m_front = 0;
25 m_size = 0;
26 m_back = -1;
27 free(m_queue);
28 }
29
30 // 从队尾插入一个数据节点
31 // 参数:i 待插入节点
32 // 返回值:true 插入成功
33 // false 插入失败,表示数据节点个数达到最大值
34 bool push_back(int i)
35 {
36 if(m_size >= m_max_size) return false;
37 m_queue[++m_back%m_max_size] = i;
38 m_back %= m_max_size;
39 m_size++;
40 return true;
41 }
42
43 // 从队首移除一个数据节点
44 // 返回值:true 移除成功
45 // false 移除失败,表示数据节点个数为0
46 bool pop_front()
47 {
48 if(m_size<=0) return false;
49 m_front = (m_front+1) % m_max_size;
50 m_size--;
51 return true;
52 }
53
54 // 获取队首节点值,不移除数据
55 int front()
56 {
57 return m_queue[m_front];
58 }
59
60 // 获取队尾节点值,不移除数据
61 int back()
62 {
63 return m_queue[m_back];
64 }
65
66 // 获取数据节点数量
67 // 返回值:数据节点数量
68 int size()
69 {
70 return m_size;
71 }
72
73 // 显示所有存在数据
74 bool show()
75 {
76 for(int i = m_front; i <= m_back; i++) cout << m_queue[i] << " ";
77 cout << endl;
78 }
79
80 private:
81 int* m_queue;
82 int m_max_size;
83 int m_front;
84 int m_back;
85 int m_size;
86 };
87
88 int main()
89 {
90 int t;
91 cin >> t;
92
93 while(t--)
94 {
95 int max_size;
96 cin >> max_size;//输入指定队列的最大节点数K
97
98 int push_num;
99 cin >> push_num;//输入指定插入的节点数量M
100
101 node_buffer queue(max_size);
102 vector<int> data(push_num,0);
103 for(int i=0; i<push_num; i++) cin >> data[i];//输入指定插入的节点数值,使用空格隔开
104
105 if (push_num > max_size) push_num = max_size;
106 for(int i=0; i<push_num; i++) queue.push_back(data[i]);
107
108 int pop_num;
109 cin >> pop_num;//输入指定移除的节点数量N
110
111 if(pop_num > queue.size()) pop_num = queue.size();
112 for(int i=0; i<pop_num; i++) queue.pop_front();
113
114 queue.show();
115 }
116 return 0;
117 }
第二题:

1 #include <cstdio>
2
3 double handle_data_func(double M,double N,double X,double &T1)
4 {
5 double v = M - N;
6 double T0;
7 T0 = (0.8 * X)/v + (0.2 * X)/N;
8 T1 = (0.2 * X)/v + (0.2 * X)/N;
9 return T0;
10 }
11
12 int main()
13 {
14 int t;
15 scanf("%d",&t);
16 double m, n, x;
17 double T0,T1;
18 while(t--)
19 {
20 scanf("%lf %lf",&m,&n);
21 scanf("%lf",&x);
22 T0 = handle_data_func(m, n, x, T1);
23 printf("%.2f \\n",T0);
24 printf("%.2f \\n",T1);
25 }
26 return 0;
27 }
第三题:

1 #include <stdio.h>
2 #include <stdbool.h>
3
4 bool is_magicnum(int number)
5 {
6 char arr[10] = {};
7 int j = 0;
8 int sumi = 0;
9 int sumj = 0;
10
11 while(number)
12 {
13 arr[j++] = number%10;
14 number /= 10;
15 }
16 j--;
17
18 for(int i=0; i<=j; )
19 {
20 if(sumi >= sumj)
21 {
22 sumj += arr[j--];
23 }
24 else if(sumi < sumj)
25 {
26 sumi += arr[i++];
27 }
28 }
29 if(sumi == sumj)
30 {
31 return true;
32 }
33 else
34 {
35 return false;
36 }
37 }
38
39 int main()
40 {
41 int t;
42 scanf("%d",&t);
43
44 int num[t];
45 for(int i=0; i < t; i++)
46 {
47 scanf("%d",&num[i]);
48 }
49 for(int i=0; i < t; i++)
50 {
51 printf("%d\\n",is_magicnum(num[i]));
52 }
53 return 0;
54 }
第四题:

1 #include <stdio.h>
2
3 int result[100000];
4 int count;
5
6 void combination(int* arr,int i,int cnt)
7 {
8 if(i >= cnt)
9 {
10 int sum = 0;
11 for(int j=0; j<cnt; j++)
12 {
13 sum += arr[j];
14 }
15 for(int j=0; j<count; j++)
16 {
17 if(sum == result[j]) return;
18 }
19 result[count++] = sum;
20 return;
21 }
22
23 int temp = arr[i];
24 arr[i] = 0;
25 combination(arr,i+1,cnt);
26 arr[i] = temp;
27 combination(arr,i+1,cnt);
28 }
29
30 int main()
31 {
32 int t = 0;
33 scanf("%d",&t);
34 while(t--)
35 {
36 int n = 0;
37 scanf("%d",&n);
38
39 int val[n];
40 for(int i=0; i<n; i++)
41 {
42 scanf("%d",&val[i]);
43 }
44
45 int num[n];
46 int cnt = 0;
47 for(int i=0; i<n; i++)
48 {
49 scanf("%d",&num[i]);
50 cnt += num[i];
51 }
52
53 int arr[n*cnt];
54 cnt = 0;
55 for(int i=0; i<n; i++)
56 {
57 for(int j=0; j<num[i]; j++)
58 {
59 arr[cnt++] = val[i];
60 }
61 }
62 printf("\\n");
63 combination(arr,0,cnt);
64 printf("%d \\n",count);
65 }
66 }
实现效果:
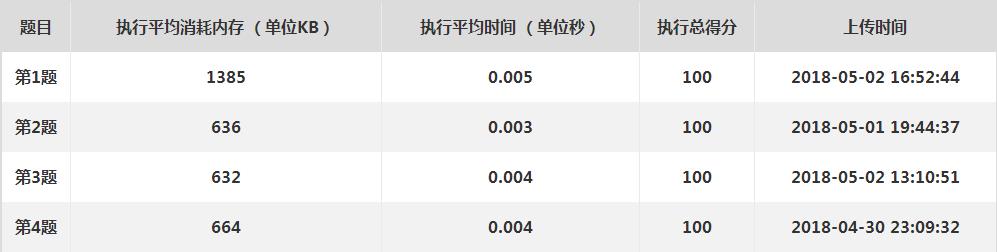
以上是关于[2018大华软件创新挑战赛]模拟赛第四题的主要内容,如果未能解决你的问题,请参考以下文章
2018大华软件大赛模拟赛第4题 (某股票操盘手账户里有N支股票,股价互不等)
2018大华软件大赛模拟赛第1题 (node_buffer定义了一个用于存储int型数据的缓冲器,请实现其声明的所有成员方法)
