深度学习——超参数调试

Posted 2020-11-02 记性不好，多记记吧

目录

• 超参数调整
• 几个超参数范围选择的方法
• 超参数的实践：pandas VS canviar
• 正则化激活函数
• softmax回归

一、超参数调整

• 重要性

从高到低：学习率$\\alpha$——>$\\beta$(0.9)、hidden units、minibatch size——>layers、学习率衰减——>$\\beta_{1}$(0.9)、$\\beta_{2}$(0.99)、$\\epsilon$($10^{-8}$)

• 如何调整参数

不要用grid来设置选择，因为不同参数的重要性不同

	Hyperparameter2
Hyperparameter1	x	x	x	x
	x	x	x	x
	x	x	x	x
	x	x	x	x

参数的选择范围可以先确定一个大的，再缩小

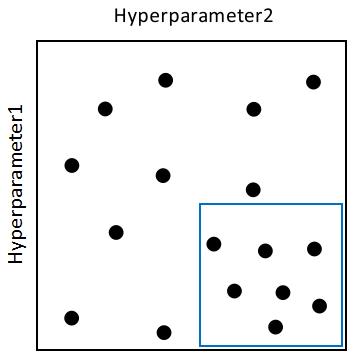
二、为超参数选择合适的范围

• uniform选择（均匀）

如每层的节点数或网络层数。但并不是适用于所有超参数

• scale的方法：比如选择学习率

如果在[0.0001,1]之间均匀选择，那么其实90%的数据是来自于[0.1,1]，10%是来自[0.0001,0.1]。为什么这个不合理？（没有找到合理的解释，是不是经验呢？）

更合理的方法应该是把[0.0001,1]转换成[-4,0] (10^-4 = 0.0001），然后在[-4,0]间取样，这样在[0.0001,0.001]和[0.1,1]间取到的数的概率更平均

更一般地，取对数，把区间写成[a,b]

• approximate scale：如指数权重均值超参数的调整

为什么直接取[0.9,0.999]是均匀分布不好：当$\\beta$越接近1时，它很小的变化会对$\\frac{1}{1-\\beta}$结果造成更大的影响

$\\beta$	0.9	0.999	0.9000	0.9005	0.999	0.9995
	10	1000
$1-\\beta$	0.1	0.001
$\\frac{1}{1-\\beta}$			10	10.05	1000	2000

调整方法：把对$\\beta$的选择，变成对$1-\\beta$的考虑，然后再进行approximate scale，转换成对次方的取值[-3, -1]

三、超参数的实践：pandas VS canviar

• pandas( babysitting one model)

一次就关注一个model，然后频繁地进行修改；系统比较复杂时选这个

• canviar(training many models in parrel)

一次可以并行调试多个model；有比较多的计算资源时选这个

四、正则化激活函数

• 正则化激活函数：对隐藏层的输入进行正则化（而不止是第一个输入层）

实现方式：batch归一化算法（这里默认对z值而不是对a）。计算出z_norm后，再求一个式子（有两个参数$\\eta$、$\\beta$），最后是用$\\tilde{z}$来计算，而$\\tilde{z}$的均值和方差可以通过两个参数来控制

给定一层的中间结果$z^{(1)}, z^{(2)}..., z^{(m)}$
$\\mu = \\frac{1}{m}\\sum_{i}z^{(i)}$ $\\sigma = \\frac{1}{m}\\sum_{i}(z_{i}-\\mu)^2$ $z^{(i)}_{norm}=\\frac{z^{(i)}-\\mu}{\\sqrt{\\sigma^2+\\epsilon}}$ $\\tilde{z}^{(i)}=\\eta z^{(i)}_{norm}+\\beta$	if $\\eta = \\sqrt{\\sigma^2+\\epsilon}$    and $\\beta = \\mu$ then $\\tilde{z}^{(i)}=z^{(i)}$

• 在nn中使用batch-norm 一般框架中会把这个实现好，如tf，只要一个函数即可

• 在mini-batch中使用bn，不考虑$b^{[l]}$

因为后面会对$z$值求平均再减去均值，这样$b^{[l]}$不论是什么值，最后都不会对结果有影响，因此这里可以不再考虑$b^{[l]}$这个参数，也就是$z^{[l]}=w^{[l]}a^{[l-1}]$。在反向求导中也不需要考虑$db^{[l]}$

• 为什么bn会有用
  • 归一化：与输入归一化的作用一致，可以加速学习
  • 就某一层来说，它的上一层对它的输入会发生变化，但是通过归一化，可以使得这个变化被限制在一定的范围（均值、方差）内，使得层与层之间可以稍微独立一点

例：对黑猫进行训练得到一个映射关系。如果把这个函数运用到对有色猫的识别，也就是输入值的分布发生了改变。那其实应该重新进行训练(covariance shift问题)

对于一个深层网络，如果考虑第$l$层，当前面的参数发生变化时，$l$层的输入也就相应变化。通过batch normalize可以让$l$层看到/处理的数据分布变得更稳定，减少了前面参数对后面层的影响。

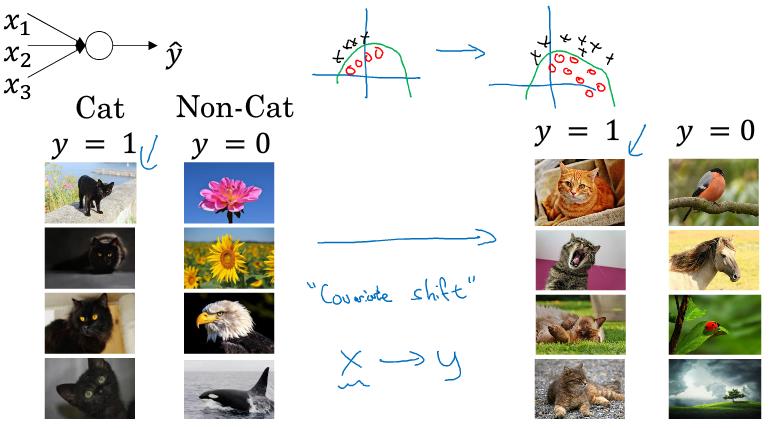
• • 副作用：正则化。每一个mini-batch是通过相应batch的均值/方差进行缩放，由此对该batch的$z$产生一些噪声，与dropout类似，从而对激活函数产生噪声，而有了正则化的效果（避免过拟合，因为后面不会过分依赖前面的参数）
• 在测试集上使用bn

训练时，bn是需要在整个mini-batch上执行，但测试时可能不能一次同时执行整个mini-batch（样本数量比较大），因此需要另外的方法进行估算

方法：指数权重平均值

五、softmax回归

相对于逻辑回归，softmax把输入分成$k$类，一般$k>2$

如下，把输入图片分成4类

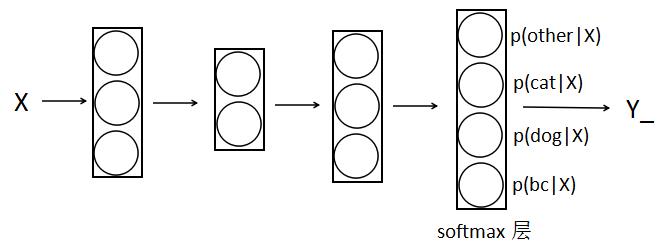
• softmax激活函数：和前面不同的是，它的输入和输出都是向量，前面只是实数；对输出结果归一化，输出的概率之和为1

$a=softmax(z)=\\begin{bmatrix}\\frac{e^{z_1}}{\\sum_{j=1}^ke^{z_j}}\\\\\\vdots  \\\\ \\frac{e^{z_k}}{\\sum_{j=1}^ke^{z_j}}\\end{bmatrix}$

例：

$z=\\begin{bmatrix}5\\\\ 2\\\\ -1\\\\3 \\end{bmatrix}$    $t=e^{z_i}=\\begin{bmatrix}e^5\\\\ e^2\\\\ e^{-1}\\\\e^3 \\end{bmatrix}=\\begin{bmatrix}148.4\\\\ 7.4\\\\ 0.4\\\\20.1 \\end{bmatrix}$    $\\sum_{j=1}^4t_j=176.3$    $a=\\frac{t}{176.3}=\\begin{bmatrix}0.842\\\\ 0.042\\\\ 0.002\\\\0.114 \\end{bmatrix}$

• hardmax

相对于hard max，它是把最可能的结果标记为1，其它为0。而softmax是通过概率大小来体现

• softmax的前向传播和反向求导过程

相关参数

$w=\\begin{bmatrix}w_{11} & ... & w_{1m}\\\\  \\vdots &  &\\vdots  \\\\  w_{k1}& ... &w_{km} \\end{bmatrix}$   $x=\\begin{bmatrix}x_1\\\\\\vdots  \\\\ x_m\\end{bmatrix}$   $b=\\begin{bmatrix}b_1\\\\\\vdots  \\\\ b_k\\end{bmatrix}$

前向传播

$z=wx+b=\\begin{bmatrix}\\sum_{i=1}^m w_{1i}x_i + b_1\\\\\\vdots  \\\\ \\sum_{i=1}^m w_{ki}x_i + b_k\\end{bmatrix}=\\begin{bmatrix}z_1\\\\\\vdots  \\\\ z_k\\end{bmatrix}$

$a=softmax(z)=\\begin{bmatrix}\\frac{e^{z_1}}{\\sum_{j=1}^ke^{z_j}}\\\\\\vdots  \\\\ \\frac{e^{z_k}}{\\sum_{j=1}^ke^{z_j}}\\end{bmatrix}=\\begin{bmatrix}a_1\\\\\\vdots  \\\\ a_k\\end{bmatrix}$

定义loss函数

$L(y, \\widehat{y})=-\\sum_{j=1}^ky_ilog\\widehat{y_i}$，其中$\\widehat{y}=a$

反向传播求导

$da_j=\\frac{dL}{a_j}=-\\frac{y_j}{a_j}$

接下来要计算：$dz_i=\\frac{dL}{z_i}$

开始时总是用$dz_i=\\frac{dL}{z_i}=\\frac{dL}{a_i}\\cdot \\frac{a_i}{z_i}$

这个其实是不对的，因为不仅$a_i$计算中用到$z_i$，在$a_j$($j\\neq i$)计算中也用到了，所以求导时要把所有$a$考虑进来，可以分成两种情况

$i = i$, $\\frac{da_i}{dz_i}=\\frac{e^{z_i}\\sum_{j=1}^ke^{z_j}-(e^{z_i})^2}{(\\sum_{j=1}^ke^{z_j})^2}=a_i-a_i^2$

$i \\neq j$, $\\frac{da_j}{dz_i}=-\\frac{e^{z_i}e^{z_j}}{(\\sum_{j=1}^ke^{z_j})^2}=-a_ia_j$

由上面两种情况合并可得：

$dz_i=\\frac{dL}{da_i}\\cdot\\frac{da_i}{dz_i}+\\sum_{j\\neq i}\\frac{dL}{da_j}\\cdot \\frac{da_j}{dz_i}\\\\=\\frac{-y_i}{a_i}(a_i-a_i^2)+\\sum_{j\\neq i}\\frac{y_j}{a_j} a_ia_j\\\\=-y_i+a_iy_i+a_i\\sum_{j\\neq i}y_j\\\\=-y_i+ai\\sum_{j=1}^ky_j\\\\=a_i-y_i$

最后一步计算中，$y_j$求和为1，是因为一个输入只属于一种分类，也就是只有一个$y_i$取值为1，其它则为0