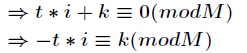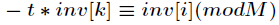逆元的认知与应用——处理除数很大的时候
Posted shuaihui
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了逆元的认知与应用——处理除数很大的时候相关的知识,希望对你有一定的参考价值。
1.什么是逆元
当求解公式:(a/b)%m 时,因b可能会过大,会出现爆精度的情况,所以需变除法为乘法:
设c是b的逆元,则有b*c≡1(mod m);///b*c%m=1%m;
则(a/b)%m = (a/b)*1%m = (a/b)*b*c%m = a*c(mod m);
即a/b的模等于a*b的逆元的模;
逆元就是这样应用的.
2.求逆元的方法。
(1).费马小定理
在是素数的情况下,对任意整数都有。
如果无法被整除,则有。
可以在为素数的情况下求出一个数的逆元,,即为逆元。
题目中的数据范围1<=x<=10^9,p=1000000007,p是素数;
所以x肯定就无法被p整除啊,所以最后就得出x^(p-2)为x的逆元啦。
但是似乎还有个问题?如何判断a是否有逆元呢?
检验逆元的性质,看求出的幂值x与a相乘是否为1即可
当p比较大的时候需要用快速幂求解
复杂度O(logn);

const int mod = 1000000009; long long qpow(long long a,long long b) { if(b<0) return 0; long long res=1; a%=mod; while(b) { if(b & 1) res=(res*a)%mod; b >>= 1; a=(a*a)%mod; } return res; } long long inv(long long a) { return qpow(a,mod-2); }
(2) 扩展欧几里得
给定模数m,求a的逆相当于求解ax=1(mod m)
这个方程可以转化为ax-my=1
然后套用求二元一次方程的方法,用扩展欧几里得算法求得一组x0,y0和gcd
检查gcd是否为1
gcd不为1则说明逆元不存在
若为1,则调整x0到0~m-1的范围中即可
PS:这种算法效率较高,常数较小,时间复杂度为O(ln n)
可扩展欧几里得求逆元ax≡1(mod n)其中a,n互质;

ll ecgcd(ll a,ll b,ll &x,ll &y) { if(b==0) { x=1; y=0; return a; } else { ll r=ecgcd(b,a%b,x,y); ll temp=x; x=y; y=y-a/b*temp; return r; } } ll inv(ll a,ll n) { ll x,y; exgcd(a,n,x,y); x = (x%n+n)%n; return x; }
(3)逆元打表法
有时会遇到这样一种问题,在模质数p下,求1~n逆元 n< p(这里
它的推导过程如下,设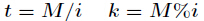
对上式两边同时除
再把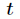
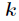
初始化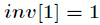

另外有个结论


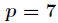
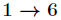
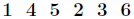

const int n=le5+5; int inv[n]; void inverse(int n,int p) { inv[1]=1; for(int i=2 ; i<=n ;i++) { inv[i]=(ll)(p-p/i)*inv[p%i]%p; } }
补充习题练手处:https://blog.csdn.net/acdreamers/article/details/8220787
以上是关于逆元的认知与应用——处理除数很大的时候的主要内容,如果未能解决你的问题,请参考以下文章