FFT求卷积(多项式乘法)
卷积
如果有两个无限序列a和b,那么它们卷积的结果是:\\(y_n=\\sum_{i=-\\infty}^\\infty a_ib_{n-i}\\)。如果a和b是有限序列,a最低的项为a0,最高的项为an,b同理,我们可以把a和b超出范围的项都设置成0。那么可以得出:y0=a0b0,y1=a1b0+a0b1,y2=a0b2+a1b1+a2b0……,y(n+m)=a(n)b(m)。
构造两个多项式A(x)和B(x):
\\(A=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}+a_nx^n\\),
\\(B=b_0+b_1x+b_2x^2+...+b_{m-1}x^{m-1}+b_mx^m\\)。
那么\\(A(x)*B(x)=C(x)=a_0b_0+(a_0b_1+a_1b_0)x+...+a_nb_mx^{n+m}\\),把系数提取出来,可以发现两序列卷积可以转换为用序列作系数进行多项式乘法。
多项式
一个多项式既可以用系数表示,也可以用点值表示。n个点可以表示一个n-1次多项式。
如果用系数表示法来多项式乘法,时间复杂度是\\(O(n^2)\\)的,而用点值表示法只需要\\(O(n)\\)的时间。然而我们需要的是系数表示法。所以我们需要找到一个优秀的算法将它们两者转换,这就是(我们眼中的)FFT。
复数
设\\(i^2=-1\\),a,b为实数,形如\\(a+bi\\)的数叫做复数。
用x轴表示a的大小,y轴表示b的大小,构造出的平面直角坐标系叫做复平面。复数的模长是原点到\\((a, b)\\)的距离,即\\(\\sqrt{a^2+b^2}\\)。复数的辐角即为以逆时针为正方向,从x轴正半轴到已知向量的转角。
复数的加减法则是显然的,可以看作向量的加减。
复数可以写成\\(N(cos\\alpha+isin\\alpha )\\),\\(\\alpha\\)表示复数的辐角。设\\(z_1=A(cos\\alpha + isin\\alpha)\\),\\(z_2=B(cos\\beta + isin\\beta)\\),那么\\(z_1z_2=AB[(cos\\alpha cos\\beta-sin\\alpha sin\\beta)+i(sin\\alpha cos\\beta+cos\\alpha sin\\beta)]=AB[cos(\\alpha+\\beta)+isin(\\alpha+\\beta)]\\)。也就是说,两复数相乘,模长相乘,辐角相加。如果写成普通形式的话,就是\\((a+bi)(c+di)=(ac-bd)+(bc+ad)i\\)。
单位根
在复平面上,以原点为圆心,1为半径作圆,所得得圆为单位圆。从x轴正半轴开始将圆n等分,联向第一个等分点所代表的复数\\(\\omega_n\\)叫做n次单位根,意思是说\\(w_n\\)的n次方为1(根据复数的乘法运算法则)。可以推得,其他等分点代表的向量为\\(\\omega_n^1\\),\\(\\omega_n^2\\)……,一直到\\(\\omega_n^n = \\omega_n^0=1\\)。显然\\(\\omega_n^k=cosk*\\frac{2\\pi}{n}+isink*\\frac{2\\pi}{n}\\)。
单位根有几个性质:
- 消去引理:\\(\\omega_{2n}^{k+n}=-\\omega_{2n}^k\\)。这是最重要的性质,使得分叉个数为2。
- 折半引理:\\({(\\omega_n^k)^2}={\\omega_{n/2}^k}\\)。这保证了FFT中子问题和原问题的规模都是n。
- 求和引理:\\(\\sum_{i=0}^{n-1}(\\omega_n^k)^i=\\left\\{ \\begin{aligned} 0, n\\nmid k \\\\ n, n\\mid k \\end{aligned} \\right.\\)这是用来证明逆变换的。
DFT
前面说过,DFT是要把多项式的系数表达转成点值表达。设多项式A(x)的系数为\\((a_o,a_1,a_2,\\ldots,a_{n-1})\\),那么
\\(A(x)=a_0+a_1*x+a_2*{x^2}+a_3*{x^3}+a_4*{x^4}+a_5*{x^5}+ \\dots+a_{n-2}*x^{n-2}+a_{n-1}*x^{n-1}\\)
将下标按照奇偶性分类,那么:\\(A(x)=(a_0+a_2*{x^2}+a_4*{x^4}+\\dots+a_{n-2}*x^{n-2})+(a_1*x+a_3*{x^3}+a_5*{x^5}+ \\dots+a_{n-1}*x^{n-1})\\)
设:
\\(A_1(x)=a_0+a_2*{x}+a_4*{x^2}+\\dots+a_{n-2}*x^{\\frac{n}{2}-1}\\)
\\(A_2(x)=a_1+a_3*{x}+a_5*{x^2}+ \\dots+a_{n-1}*x^{\\frac{n}{2}-1}\\)
那么:\\(A(x)=A_1(x^2)+xA_2(x^2)\\)
根据单位根的性质,将前面一半的值带入可得:
\\(A(\\omega_n^k)=A_1(\\omega_n^{2k})+\\omega_n^kA_2(\\omega_n^{2k})=A_1(\\omega_{\\frac{n}{2}}^{k})+\\omega_n^kA_2(\\omega_{\\frac{n}{2}}^{k})\\)(折半引理的作用:将问题分解成条件完全相同的子问题)
同理带入后面的值:
\\(A(\\omega_n^{k+\\frac{n}{2}})=A_1(\\omega_n^{2k+n})+\\omega_n^{k+\\frac{n}{2}}(\\omega_n^{2k+n})=A_1(\\omega_n^{2k})-\\omega_n^kA_2(\\omega_n^{2k})\\)(消去引理:使得分叉个数为2。如果没有这个引理的话,就必须再去算一遍\\(A(\\omega_n^{k+\\frac{n}{2}})\\)的值,分叉个数变成4了。)
由于这两个式子只有加号减号不同,我们只需计算前面一半的点值即可。这样就将问题规模缩小了一半。当n=1时,点值是一个常数,直接返回即可。不难看出这是一个分治算法,时间复杂度为\\(O(nlogn)\\)。
为IDFT作准备
我们发现,FFT其实是在求下图的\\(y_i\\):(实在打不出来qwq)

那么现在的问题是,已知\\(y_i\\),如何推回\\(a_i\\)?
由于我太弱了,继续上图吧。。

(补充一下,只要求出那个范德蒙德行列式的逆矩阵,乘在等式两边,那么就可以通过\\(y_i\\)推出\\(a_i\\))
怎么构造\\(V^{-1}\\),使得\\(v_i^Tv_j^{-1}=\\left\\{ \\begin{aligned} 1, i=j \\\\ 0, i\\ne j\\end{aligned} \\right.\\)呢?
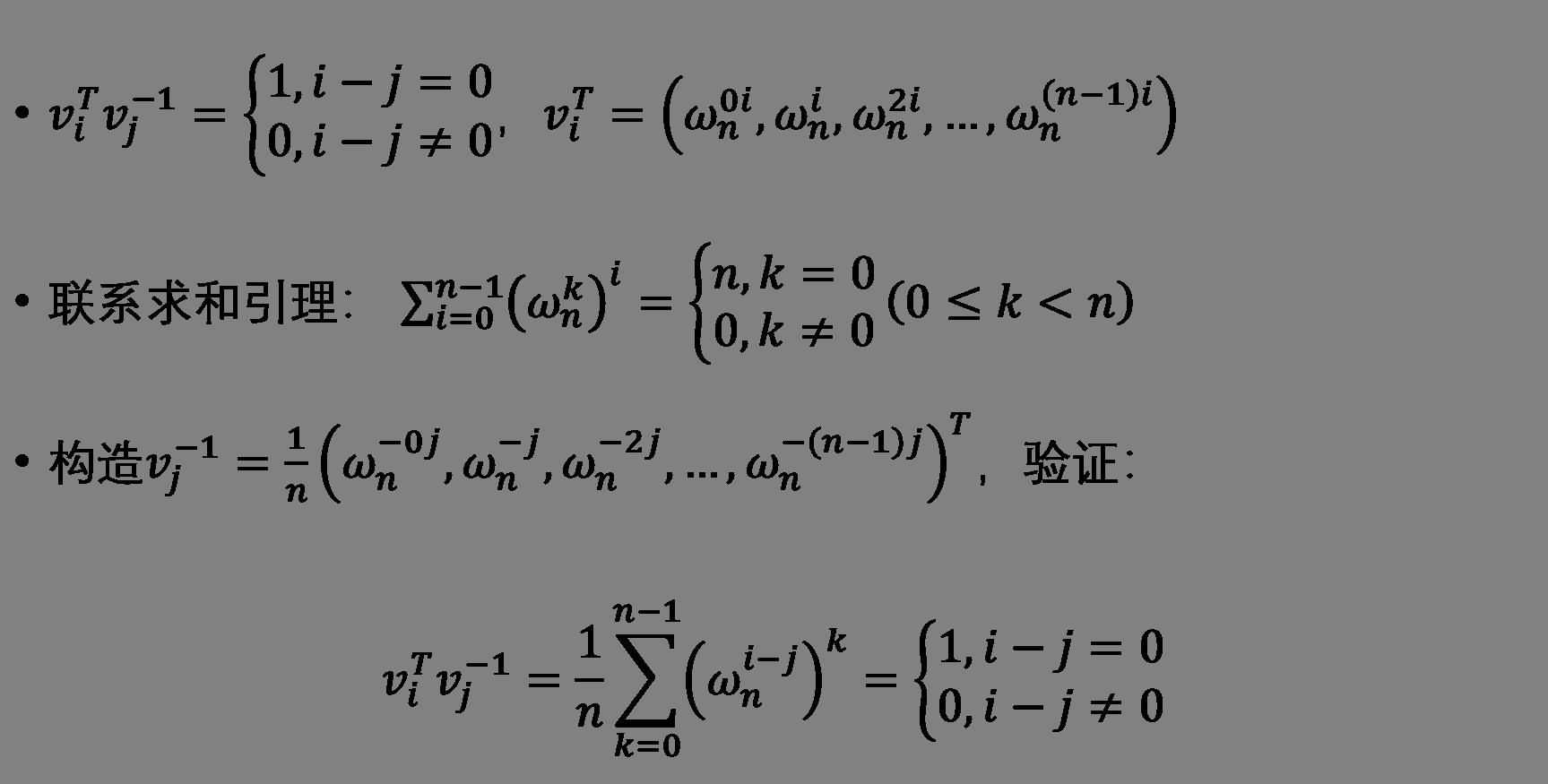
是不是很神?这样我们就构造出了\\(V^{-1}\\):

现在,问题就变成了用\\(\\omega_n^{-1}\\)为本原单位根,对y向量作FFT以后除以n。PPT里说的吼啊,稍微修改一下代码就行了。
递归实现FFT
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=2e6+5;
const double Pi=3.1415926535898;
int t, n, m, len=1;
struct Cpx{ //复数
double x, y;
Cpx (double t1=0, double t2=0){ x=t1, y=t2; }
}A[maxn*2], B[maxn*2], C[maxn*2];
Cpx operator +(Cpx a, Cpx b){ return Cpx(a.x+b.x, a.y+b.y); }
Cpx operator -(Cpx a, Cpx b){ return Cpx(a.x-b.x, a.y-b.y); }
Cpx operator *(Cpx a, Cpx b){ return Cpx(a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x); }
void fdft(Cpx *a, int n, int flag){ //快速将当前多项式从系数表达转换为点值表达
if (n==1) return; //如果只有1项系数为k,唯一的点值就是(w[1,1],k*w[1,1])=(1, k)
Cpx a1[(n>>1)+1], a2[(n>>1)+1];
for (int i=0; i<(n>>1); ++i) a1[i]=a[i<<1], a2[i]=a[i<<1|1];
fdft(a1, n>>1, flag); fdft(a2, n>>1, flag);
Cpx w1(cos(2*Pi/n), flag*sin(2*Pi/n)), w(1, 0); //idft用的负根
for (int i=0; i<(n>>1); ++i, w=w*w1){
a[i]=a1[i]+w*a2[i];
a[i+(n>>1)]=a1[i]-w*a2[i];
}
}
int main(){
scanf("%d%d", &n, &m); int x;
for (int i=0; i<=n; ++i) scanf("%lf", &A[i].x);
for (int i=0; i<=m; ++i) scanf("%lf", &B[i].x);
while (len<n+m) len<<=1; //idft需要至少l1+l2个点值
fdft(A, len, 1); fdft(B, len, 1);
for (int i=0; i<len; ++i) C[i]=A[i]*B[i];
fdft(C, len, -1); //idft
for (int i=0; i<=n+m; ++i){
x=C[i].x/len+0.5;
printf("%d ", x);
}
return 0;
}
题目是luogu的模板。注意给出的n和m都是多项式的最高次数,也就是说乘起来后的多项式最高次数为n+m,至少需要n+m个点。
迭代版FFT
递归版的太慢了,暗中观察我们是如何处理序列的,可以发现:

把每个元素的编号二进制反转一下,就是我们要求的序列编号!原因是原序列的最后1位决定了当前元素被分到前半区还是后半区,也就是转换后元素编号的第1位。依次类推。
有一个O(n)推出n个数各自编号镜像反转的方法,大体思想是通过i<<1的反转推出i的反转。
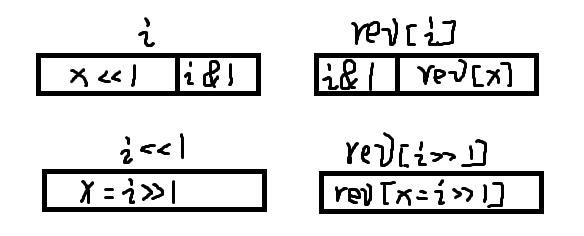
由于各种原因,迭代版要比递归版快四倍左右~
#include <cmath>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=2e6+5;
const double pi=3.1415926535898;
int t, n, m, len=1, l, r[maxn*2];
struct Cpx{ //复数
double x, y;
Cpx (double t1=0, double t2=0){ x=t1, y=t2; }
}A[maxn*2], B[maxn*2], C[maxn*2];
Cpx operator +(Cpx a, Cpx b){ return Cpx(a.x+b.x, a.y+b.y); }
Cpx operator -(Cpx a, Cpx b){ return Cpx(a.x-b.x, a.y-b.y); }
Cpx operator *(Cpx a, Cpx b){ return Cpx(a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x); }
void fdft(Cpx *a, int n, int flag){ //快速将当前多项式从系数表达转换为点值表达
for (int i=0; i<n; ++i) if (i<r[i]) swap(a[i], a[r[i]]);
for (int mid=1; mid<n; mid<<=1){ //当前区间长度的一半
Cpx w1(cos(pi/mid), flag*sin(pi/mid)), x, y;
for (int j=0; j<n; j+=(mid<<1)){ //j:区间起始点
Cpx w(1, 0);
for (int k=0; k<mid; ++k, w=w*w1){ //系数转点值
x=a[j+k], y=w*a[j+mid+k];
a[j+k]=x+y; a[j+mid+k]=x-y;
}
}
}
}
inline int getint(int &x){
char c; int flag=0;
for (c=getchar(); !isdigit(c); c=getchar())
if (c==\'-\') flag=1;
for (x=c-48; c=getchar(), isdigit(c);)
x=(x<<3)+(x<<1)+c-48;
return flag?x:-x;
}
int main(){
getint(n); getint(m); int x;
for (int i=0; i<=n; ++i) getint(x), A[i].x=x;
for (int i=0; i<=m; ++i) getint(x), B[i].x=x;
while (len<=n+m) len<<=1, ++l; //idft需要至少l1+l2个点值
for (int i=0; i<len; ++i) //编号的字节长度为l
r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
fdft(A, len, 1); fdft(B, len, 1);
for (int i=0; i<len; ++i) C[i]=A[i]*B[i];
fdft(C, len, -1); //idft
for (int i=0; i<=n+m; ++i) printf("%d ", int(C[i].x/len+0.5));
return 0;
}
这样可以做到1e6的数据最差也能跑进1s。我太菜了,并不会什么常数优化。
两个月后的PS:注意n个点确定一个n-1次多项式。这是因为,对多项式求点值表达,相当于将一个范德蒙德矩阵乘上系数矩阵(前文有图)。而范德蒙德矩阵是可逆的,所以在已知y的情况下,a也是唯一确定的。因此n个点一定唯一确定一个n-1次多项式。
五个月后的PS:qwq 借用了不少大佬的东西,侵删。