决策树

Posted 2020-11-01 haofeng5

 

 

决策树的主流算法有很多种，接触一种记录一种。

一、CART：二叉树，一个节点一般分出左右两个孩子。通过Gini index决定最优分割。如果我们想对某一Node进行分割，先测量分割前node 的基尼系数，再测量按照某一准则（如I{X<=c}）分割后左右两字数的基尼系数之和，两者相减则为不纯程度（Imputiry）下降的分数。具体计算基尼系数的分数是：

 

 二、香农熵（Shannon entropy），进化版本为ID3->C4.5->C5.0。主要原则是利用一个节点内熵的变化衡量纯度变动。熵的计算公式为

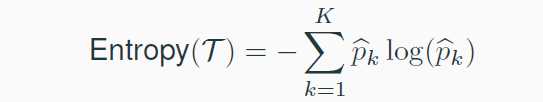
类似的，衡量节点分割前的香农熵，以及节点分割后各个分区的香农熵之和，两者之差被定义为信息增益（information gain）。值得注意的是，C5.0算法可以create multiple child nodes from one node。

三、Misclassification error。没有详细了解，应该是通过计算分割前后的误差之差决定最优分割。

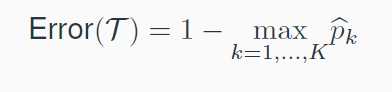
 三者对比。个人认为该图片仅考虑了两个类的数据分割情况。p代表结点中某一类的占比。可以看到纯度随着结点中A类占比的增大呈现先上升后下降的趋势。并且都在五五分割的时候不纯程度（Impurity）最大。

 

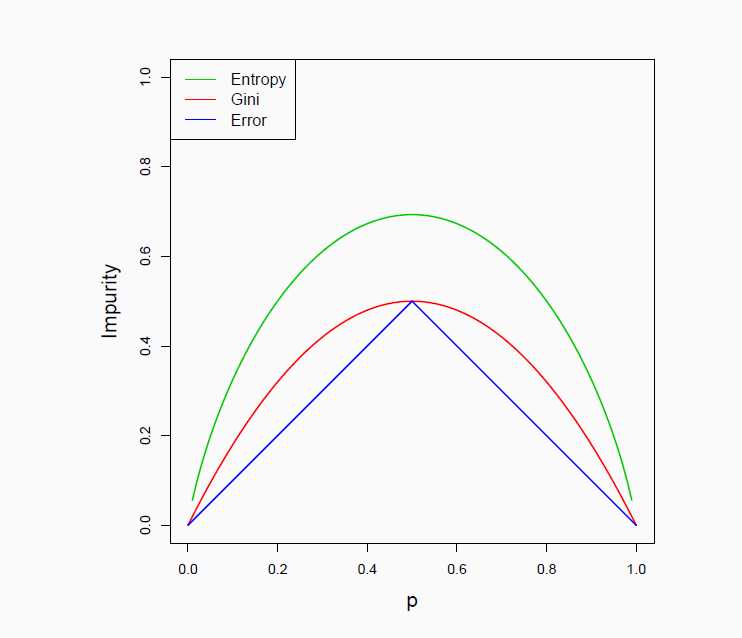
通过三者特性得出以下的对比结论：

1. 基尼系数和香农熵对于node probability的改变更为敏感（表现在图上就是曲线的斜率更大，更为陡峭），因此，这两种度量方法旨在寻找更为"pure“的nodes。

2. Misclassification error可以用来评估一棵树的情况，但是对于构造决策树，略微有些敏感度不足了。

 

对于categorical predictors的分类，原理相同，对于一个取值范围再1,...,Md的名义变量我们寻找它取值范围的子集A。这时候我们的splitting rule为：I{X belongs to A}

可以看到，我们有至多2^(M-1)-1中分类。

（注，分类的组合为Cm1+Cm2+...+Cm(m/2)中，注意把一个set 分为1/4 和分为4/1的结果是一样的，顶多树的左右子节点位置互换而已没有意义，因此不是Cm1+...+Cm(m-1)。但是Cm1+Cm2+...+Cm(m/2)=1/2(Cm1+...Cm(m-1))。所以我们通过求后者来计算前者。这个式子的解法运用到高中排列知识的二次项定理，(1+1)^m 的系数正好是Cm0+Cm1+Cm2+...+Cmm。

 

恩……为啥是横的。随便吧。这个分类数目是非常大的（computationally intense）。因此一种启发式的思想是对某一子节点采用randomly sample的方法选择子集，然后比较这几个随机splitting的分类结果。

当outcome y是连续性的时候，可以理解为我们在做回归。这时候我们同意需要新的Impurity度量方法。通过加权方差减少量来度量。

 

综上，三种情况，输入变量是连续性变量，输入变量是分类变量，输出变量是连续性变量。前两种情况的不同主要是最优分类的分类准则不同，对于分类后的分数计算和比较都是一样的。第三种情况主要是分类后的分数计算要用连续性的方差来衡量。

 

对于决策树的总结；

 

下面探讨一下修剪(pruning)树的问题

1. 提前停止法（early stopping），或者成为预剪枝法(pre-prunning）。这种方法避免了做不必要的工作，但是缺点在于没有办法直到决策树时候都会错细微但重要的模式，因为这种细微模式只有决策树生长到足够大时才能学到。

2. 后剪枝决策树法（post-pruning）。先生成一颗较大的决策树，再进行修剪将决策树减小到合适的大小。该方法通常比预剪枝法更有效，因为如果没有事先生成决策树，那么决定一棵决策树生长的最优程度是相当困难的，而事后修剪决策树可以试算法发现所有重要的数据结构。

C5.0算法的优点之一在于它可以自动修剪。它关注许多决策，能自动使用相当合理的默认值。该算法的总体决策就是事后修剪决策树。它先生成一个过度拟合训练数据的大决策树，然后删除对分类误差影响不大的节点和分枝。在某些情况下， 整个分枝会被进一步向上移动或者被一些简单的决策所取代，这两种移植分枝的过程分别称为子树提升(subtree raising）和子树替换（subtree replacing）。