模板矩阵快速幂

Posted 2020-11-01 ztz11

矩阵加速运算，快速幂

题目背景

矩阵快速幂

题目描述

给定n*n的矩阵A，求A^k

输入输出格式

输入格式：

第一行，n,k

第2至n+1行，每行n个数，第i+1行第j个数表示矩阵第i行第j列的元素

输出格式：

输出A^k

共n行，每行n个数，第i行第j个数表示矩阵第i行第j列的元素，每个元素模10^9+7

说明

n<=100, k<=10^12, |矩阵元素|<=1000 算法：矩阵快速幂

思路：

一道模板矩阵快速幂

首先理解一下什么是矩阵乘法

比如说f[][]矩阵乘j[][]，设答案矩阵为ans[2][2]

则ans[1][1]=f[1][1]*j[1][1]+f[1][2]*j[2][1]+.....+f[1][k]*j[k][1]

ans[1][2]=f[1][1]*j[1][2]+f[1][2]*j[2][2]+.....+f[1][k]*j[k][2]

。

。

。

也就是说ans[a][b]=Σf[a][1~k]的每一个元素乘上j[1~k][b]的每个元素

如图：

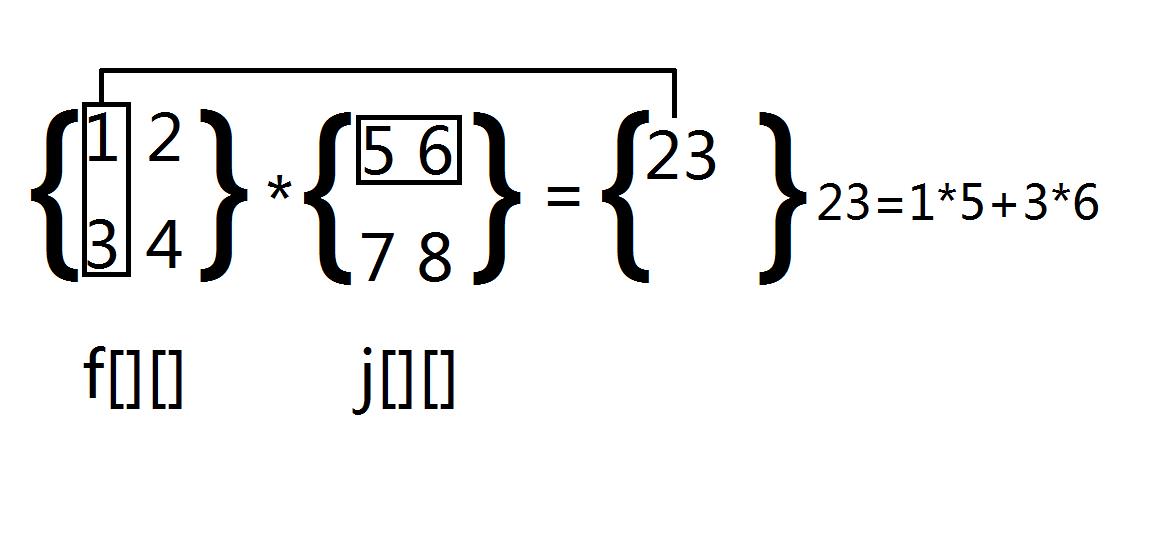
任务的一半结束，但还差快速幂

我相信你不会天真到在k=10^12的情况下还o(k)地扫一遍

怎么办？？
快速幂来救场

 关于快速幂可详见我的另一篇博客

时间降到o(logn);

过了

代码：

#include<iostream>
#include<cstdio>
#define rii register int i
#define rij register int j
#define rik register int k
using namespace std;
long long x[105][105],zcq[105][105],ls[105][105],n,k,mod=1e9+7;
void cf2()
{
    long long ans=0;
    for(rii=1;i<=n;i++)
    {
        for(rij=1;j<=n;j++)
         {
            ls[i][j]=zcq[i][j];
         }
    }
    for(rii=1;i<=n;i++)
    {
        for(rij=1;j<=n;j++)
        {
            for(rik=1;k<=n;k++)
            {
                ans+=(x[i][k]*ls[k][j])%mod;
                ans=ans%mod;
            }
            zcq[i][j]=ans%mod;
            ans=0;
        }
    }
}
void cf1()
{
    long long ans=0;
    for(rii=1;i<=n;i++)
    {
        for(rij=1;j<=n;j++)
        {
            ls[i][j]=x[i][j];
        }
    }
    for(rii=1;i<=n;i++)
    {
        for(rij=1;j<=n;j++)
        {
            for(rik=1;k<=n;k++)
            {
                ans+=(ls[i][k]*ls[k][j])%mod;
                ans=ans%mod;
            }
            x[i][j]=ans%mod;
            ans=0;
        }
    }
}
void ksm(long long k)
{
    if(k==0)
    {
        return;
    }
    if(k%2==0)
    {
        cf1();
        ksm(k/2);
        return; 
    } 
    else
    {
        cf2();
        ksm(k-1);
        return;
    }
}
int main()
{
    scanf("%lld%lld",&n,&k);
    for(rii=1;i<=n;i++)
    {
        for(rij=1;j<=n;j++)
        {
            scanf("%d",&x[i][j]);
            zcq[i][j]=x[i][j];
        }
    }
    ksm(k-1);
    for(rii=1;i<=n;i++)
    {
        for(rij=1;j<=n;j++)
        {
            printf("%ld ",zcq[i][j]);
        }
        printf("\\n");
    }
}