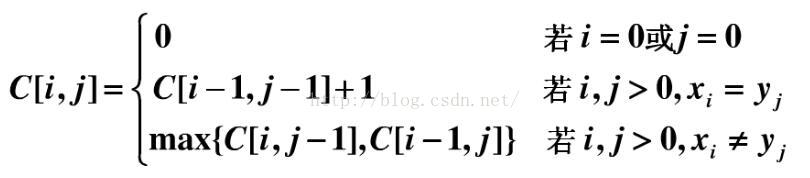最长公共子序列-golang

Posted 2020-11-01 走走停停

题目：

给定两个字符串str1和str2，返回两个字符串的最长公共子序列

举例：

str1 = "1A2C3D4B56"

str2 = "B1D23CA45B6A"

它们的最长公共子序列为："123456" 或 "12C4B6"

解题方法：

经典的动态规划方法：

根据状态方程可以得到由str1和str2生成的状态数组dp，代码如下：

func GetDp(arr1, arr2 []rune)[][]int{
    dp := make([][]int, len(arr1))
    for k, _ := range dp{
        dp[k] = make([]int, len(arr2))
    }
    if arr1[0] == arr2[0]{
        dp[0][0] = 1
    }else{
        dp[0][0] = 0
    }
    for i:=1;i<len(arr1);i++{//计算第一列
        if arr1[i] == arr2[0]{
            dp[i][0] = 1
        }else{
            dp[i][0] = dp[i-1][0]
        }
    }
    for i:=1;i<len(arr2);i++{//计算第一行
        if arr2[i] == arr1[0]{
            dp[0][i] = 1
        }else{
            dp[0][i] = dp[0][i-1]
        }
    }
    for i:=1;i<len(arr1);i++{//其余部分
        for j:=1;j<len(arr2);j++{
            if arr1[i] == arr2[j]{
                dp[i][j] = dp[i-1][j-1]+1
            }else{
                dp[i][j] = getMax(dp[i-1][j], dp[i][j-1])
            }
        }
    }
    return dp
}

　对于举例中的两个字符串，可以得到dp数组如下：

[ [0 0 0 0 0 0 0 1 1 1]

 [1 1 1 1 1 1 1 1 1 1] 

 [1 1 1 1 1 2 2 2 2 2]

 [1 1 2 2 2 2 2 2 2 2]

 [1 1 2 2 3 3 3 3 3 3]

 [1 1 2 3 3 3 3 3 3 3]

 [1 2 2 3 3 3 3 3 3 3]

 [1 2 2 3 3 3 4 4 4 4]

 [1 2 2 3 3 3 4 4 5 5]

 [1 2 2 3 3 3 4 5 5 5]

 [1 2 2 3 3 3 4 5 5 6]

 [1 2 2 3 3 3 4 5 5 6]]

搜索公共子序列的时候，从右下角开始，向上、左上和左三个方向移动，如果当前位置的值跟左边一个或者上边一个值相同，则向左或者向上移动，如果不等，则向左上移动，它们的差为1，搜索代码如下：

func GetRes(dp [][]int, arr1 []rune, arr2 []rune)[]rune{
    m, n := len(arr1)-1, len(arr2)-1
    res := make([]rune, dp[m][n])
    index  := len(res) -1
    for index >= 0 {
        if n>0 && dp[m][n] == dp[m][n-1]{
            n--
        }else if m > 0 && dp[m][n] == dp[m-1][n]{
            m--
        }else{
            res[index] = arr1[m]
            index --
            m--
            n--
        }
    }
    return res
}