连分数的性质

Posted 2020-11-01

大概：连分数应用于数值表示、近似计算、方程求解等方面。文章就此讨论证明连分数的某些性质。
首先让我们一起回温下数学归纳法：
数学归纳法：(证明高斯求和公式)
1， 基础情况:s(1)
2， 归纳假设:s(k)
已知：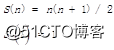
假设n=k：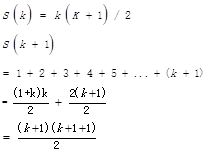
此时将n=k+1带入s(n)中验证可得：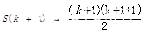
It’s amazing!
下面就进入我们主题，有意思的连分数：
连分数定义：
形如：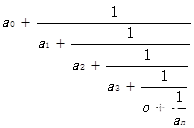

表达式，我们称之为连分数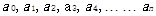称作 部分商，可以是实数或复数。项数可以有限，也可以无限。具体[1]。
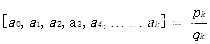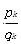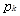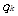一般地 ，我们称为第k位渐近分数，其中 和互质。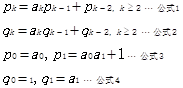

接下来用数学归纳法进行证明：

Base case: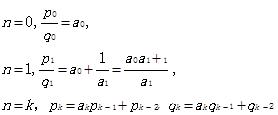


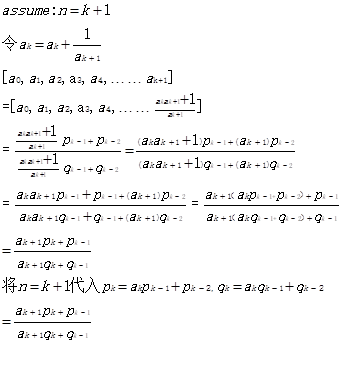
证明结束！

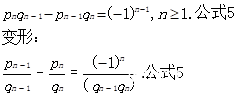
接下来用数学归纳法进行证明：
Base case: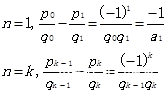


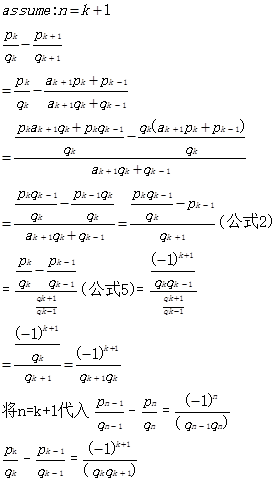
简单有穷连分数性质：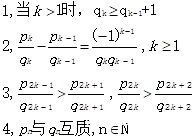

小结：
连分数中，渐近分数分母一直增大，而相邻分数差愈小，另外偶数项部分，呈现单调增，奇数项部分，单调减。

应用：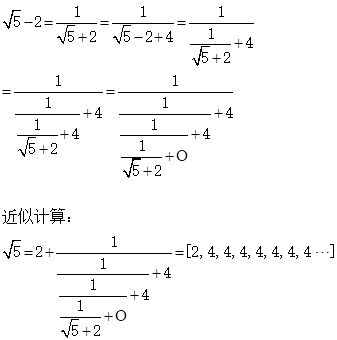

小结：
有理数可表示为有限简单连分数。
无理数可表示为无限简单连分数。
循环简单连分数所表示无理数是二次无理数。

有趣一刻：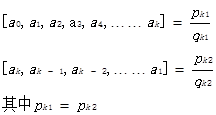

在《Proofs that Really Count》中利用组合学给出的相应的解释，在此就不叙述了。

参考文献：
[1] 连分数及其基本性质 .何雅
[2] 论连分数的应用.于海杰
[3] 连分数的一个性质以及它的组合解释
http://www.matrix67.com/blog/archives/5556
[4] 连分数的一个性质以及它的组合解释