Manacher算法 , 实例 详解 . NYOJ 最长回文

Posted 2020-07-10

51 Nod http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1089

Manacher 算法 

定义数组 p[i]表示以i为中心的(包含i个这个字符)回文串半径长.

将字符串s从前扫到后,来计算p[i] , 则最大的p[i]就是最长回文串长度 ,

由于s是从前扫描到最后的,所以需要计算p[i]时一定计算好了 p[1]~~p[i-1]

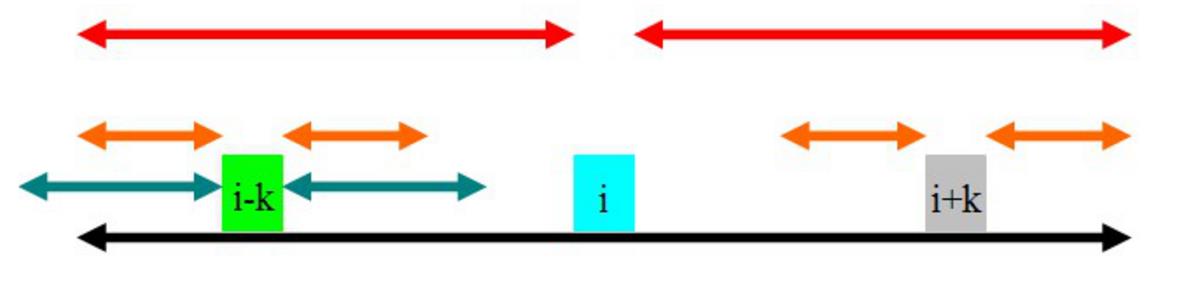
假设现在扫描到了i+k这个位置,现在需要计算p[i+k]

定义maxlen是位置i+k位置前所有回文串中能延伸到的最有右端的位置 ,即maxlen=p[i]+i; // p[i]表示半径长 , i 表示目前最长的位置 , //这有两种情况 .

1 : i+k 这个位置不在前面的任何回文串中 , 即 i+k>maxlen , 则促使换p[i+k]=1 ; //  意思就是本身就是一个回文串 , 此时的长度的为 1 --> p[i+k]=1 ; 然后p[i+k]左右延伸,即while(s[i+k+p[i+k]]==s[i+k]-p[i+k])　　　++p[i+k];  // 这样计算出来 p[i+k]的长度 .

2 : i+k 这个位置被前面以位置i为中心的回文串包含,即maxlen>i+k;这样的话p[i+k]就不是从1开始的 .        

由于回文串的性质 , 可知i+k这个位置与关于 i 的i-k对称,所以p[i+k]分为一下三种情况得出 ,  

// 黑色的是i的回文串范围,蓝色的是i-k的回文串范围.

  然后就是三种情况了  

第一种情况  :  i-k 回文串有一部分在 i 的回文串之外 , 如上图蓝色左端在黑色右端之外 , 这种情况p[i+k]=p[i]-k;  // 这时候就有人会有疑惑了 , p[i-k]那里的长度比你上面上的p[i]-k要长呀 ? 很正确虽然p[i-k]的长度长但是 p[i]的延伸最终在那里终止了 就说明 i+p[i]和i-p[i]是不相同的两个符号 , 所以p[i+k]的长度最多只是 , p[i]-k;

第二种情况  :  i-k的回文串全部在p[i]之内 , 所以p[i+k]=p[i-k]那么这是的p[i+k]会不会更长呢 , 不可能 原因的话自己想想 . 

第三种情况  :  i-k的右端和i的右端重合 , 这时候 p[i+k]最小是p[i]-k ; 并且可能继续增加 . 

  //  NYOJ 的答案

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
#include<set>
#include<stack>
#include<string>
#include<sstream>
#include<map>
#include<cctype>
#include<limits.h>
using namespace std;
char s[220000];         // s  是      模式串
int p[220000];                   //             表示  以 i 为中心 情况下 最长的   长度
int main()
{
    while(scanf("%s",s)!=EOF)
    {
        memset(p,0,sizeof(p));
        int len=strlen(s),id=0,maxlen=0;                        //  字符串长度   ,
        for(int i=len;i>=0;--i)                        // 插入 # 解决 , 长度为奇偶的问题 .
        {                             //插入\'#\'
            s[i+i+2]=s[i];
            s[i+i+1]=\'#\';
        }                                       //插入了len+1个\'#\',最终的s长度是1~len+len+1即2*len+1,首尾s[0]和s[2*len+2]要插入不同的字符
        s[0]=\'*\';                                       //s[0]=\'*\',s[len+len+2]=\'\\0\',防止在while时p[i]越界
        for(int i=2;i<2*len+1;++i)   // 完善好字符串之后 ,
        {
            if(p[id]+id>i)
                p[i]=min(p[2*id-i],p[id]+id-i);  //   如果超过的话 , 右边(p[id]+id-i)的大 如果不超过的话 左边(p[2*id-i])的 大
            else
                p[i]=1;
            while(s[i-p[i]] == s[i+p[i]])    // 第 26 -- 29 , 32 33  都是为了 减小时间复杂度 来设置的 .
                p[i]++;
            if(id+p[id]<i+p[i])    // 这个 id+p[id] 是模式串中已经解决的 最右端 问题 .
                id=i;
            if(maxlen<p[i])
                maxlen=p[i];
        }
        cout<<maxlen-1<<endl;
    }
    return 0;
}