[LuoguP1005]矩阵取数游戏 (DP+高精度)

Posted 2020-11-01 GoldenPotato的OI世界

题面

传送门:https://www.luogu.org/problemnew/show/P1005

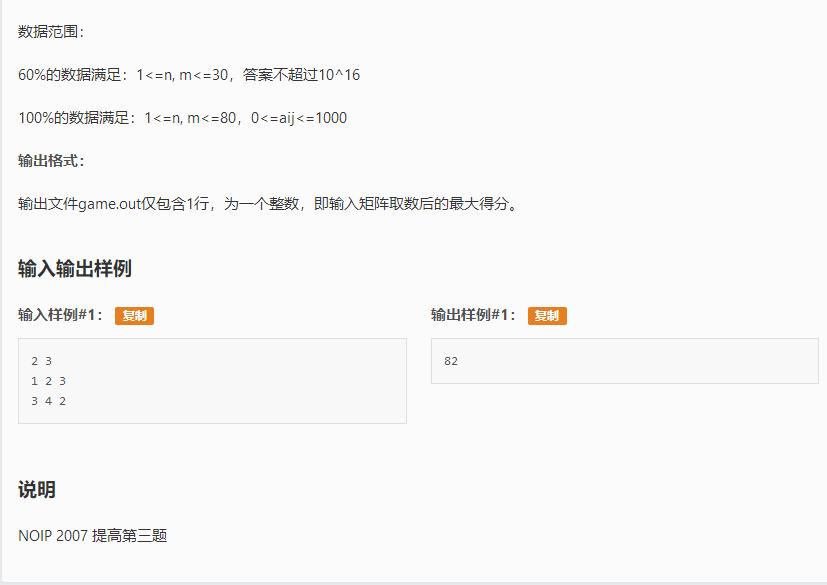
Solution

我们可以先考虑贪心

我们每一次都选左右两边尽可能小的数,方便大的放在后面

听起来挺OK的

实则并不OK

反例:

3 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 

如果贪心的话,我们会优先把右边那一串2先选了,再去选3和1

但是正确答案显然是先把3和1选了,再去选那一串2

 

---

 

既然贪心不成,我们可以考虑一下DP

然后我们考虑这样一个状态:

f[i][j][k] 表示第i时刻,第j行,左边选到了第k列

因为我们知道了当前时刻和左边选到的列数,右边选到的列数也可以推算出来: m-i+k-1

然后就可以写出来一个比较显然的转移方程:

 

f[i][j][k]=max(f[i-1][j][k-1]+2^i*num[j][k-1],f[i-1][j][k]+2^i*num[j][m-i+k]) 

也就是第i时刻是选最左边的还是选右边的

 

---

 

 

这样子我们就可以得到 100分 60分

为什么会变成这样的呢?

原因很简单,我们仔细看一下数据范围:80

也就是说数据大小至少会有2^80

显然longlong (Int64)是放不下的

 

这时候,我们就需要伟大的Int128

你当然可以用stl的int128(虽然考试中不能用)

我们这里选用手写一个高精度类

我们只需要高精乘低精,高精加高精,高精比较大小

再加上若干时间的调试高精

 

然后就OjbK了

Code

//Luogu P1005 矩阵取数游戏
//DP+高精
//Apr,27th,2018
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct Int128
{
    int a[50],len;
    Int128()
    {
        memset(a,0,sizeof a);
        len=0;
    }
    void Insert()
    {
        char c=getchar();
        while(!isdigit(c)) c=getchar();
        while(isdigit(c)){a[++len]=c-\'0\';c=getchar();}
        int tot=len/2;
        for(int i=len;i>tot;i--)swap(a[i],a[len-i+1]);
    }
    void Print()
    {
        for(int i=len;i>=1;i--)
            printf("%d",a[i]);
    }
    friend Int128 operator * (Int128 a,int b)
    {
        Int128 ans=Int128();
        ans.len=a.len;
        for(int i=1;i<=ans.len;i++)
        {
            ans.a[i]+=a.a[i]*b;
            ans.a[i+1]+=ans.a[i]/10;
            ans.a[i]%=10;
            if(i==ans.len and ans.a[i+1]!=0)
                ans.len++;
        }
        return ans;
    }
    friend Int128 operator + (Int128 a,Int128 b)
    {
        Int128 ans=Int128();
        ans.len=max(a.len,b.len);
        for(int i=1;i<=ans.len;i++)
        {
            ans.a[i]+=a.a[i]+b.a[i];
            ans.a[i+1]+=ans.a[i]/10;
            ans.a[i]%=10;
            if(i==ans.len and ans.a[i+1]!=0)
                ans.len++;
        }
        return ans;
    }
    friend bool operator < (Int128 a,Int128 b)
    {
        if(a.len<b.len) return true;
        if(a.len>b.len) return false;
        for(int i=a.len;i>=1;i--)
            if(a.a[i]>b.a[i])
                return false;
            else if(a.a[i]<b.a[i])
                return true;
        return false;
    }
};
const int N=80+10;
Int128 f[2][N][N],POW[N];
int a[N][N];
int n,m;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
            
    POW[1].len=1,POW[1].a[1]=2;
    for(int i=2;i<=m;i++)
        POW[i]=POW[i-1]*2;
    for(int i=1;i<=m;i++)
        for(int j=1;j<=n;j++)
            for(int k=1;k<=i+1;k++)
            {
                if(k>1)
                    f[i%2][j][k]=f[(i-1)%2][j][k-1]+POW[i]*a[j][k-1];
                if(m-i+k-1<m)
                    f[i%2][j][k]=max(f[i%2][j][k],f[(i-1)%2][j][k]+POW[i]*a[j][m-i+k]);
                //f[i%2][j][k].Print();
                //cout<<endl;
            }
    
    Int128 ans=Int128();
    for(int i=1;i<=n;i++)
    {
        Int128 t_ans=Int128();
        for(int j=1;j<=m;j++)
            t_ans=max(t_ans,f[m%2][i][j]);
        ans=ans+t_ans;
    }
    
    ans.Print();
    return 0;
}