分布式计算 标准差,信度
当一组数据无法完全加载到内存计算时,那我们就需要进行分布式计算,每台机器计算部分数据然后合成最后结果。例如典型的词频统计案例,但是当最后的结果不能根据每台机器的结果得出,那么就要拆分算法了。
拆分算法的标准:算法公式的粒度一定要能根据分布式的各个task处理得出
拆分标准差:
针对一组数据 (例如:1、2、3、4、5、6、7),我们把他拆分到两台机器来计算
两组数据
A机器计算 (1、2、3、4)
B机器计算 (5、6、7)
首先单组数据需要计算三个指标
针对(1、2、3、4) 这个小组:
成员个数: 4
成员之和: 1+2+3+4=10
成员的平方和:1²+2²+3²+4²=30
针对(5、6、7) 这个小组:
成员个数: 3
成员之和: 5+6+7=18
成员的平方和:5²+6²+7²=110
拿到这三个指标之后,拿mr来说,我们就可以在每个map中计算这三个指标,最后在reduce中
执行算法
((110+30)/(4+3))-((10+18)/(4+3))²
在开方就就刚好和mysql 的std计算结果一样了
代码实现:
val rdd1 = sc.makeRDD(Array(("A",1),("A",2),("A",3),("A",4),("A",5),("A",6),("A",7)))
rdd1.combineByKey(
(v : Int) => List(v,v*v,1),
(c : List[Int], v : Int) => List(c.apply(0)+v,(c.apply(1)+v*v),c.apply(2)+1),
(c1 : List[Int], c2 : List[Int]) => List(c1.apply(0)+c1.apply(0),c1.apply(1)+c1.apply(1),c1.apply(2)+c1.apply(2))
).mapValues(x => sqrt((x.apply(1)/x.apply(2)) - (x.apply(0)/x.apply(2))*(x.apply(0)/x.apply(2)))).collect().foreach(println)
def sqrtIter(guess: Double, x: Double): Double =
if (isGoodEnough(guess, x))
guess
else
sqrtIter((guess + x / guess)/2, x)
// 判断解是否满足要求
def isGoodEnough(guess: Double, x: Double) =
abs(guess * guess - x)< 0.0001
// 辅助函数,求绝对值
def abs(x: Double) =
if (x < 0) -x else x
// 目标函数
def sqrt(x: Double): Double =
sqrtIter(1, x)
来看看mysql 的结果是否一样
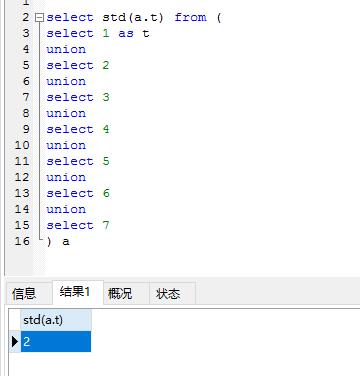
得到了标准差,信度再次基础上加上子集的计算就可以了!