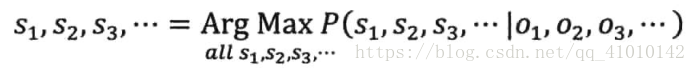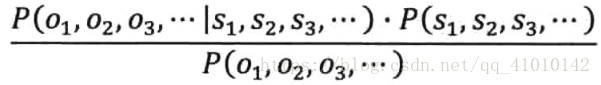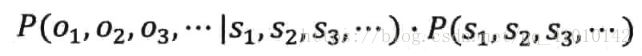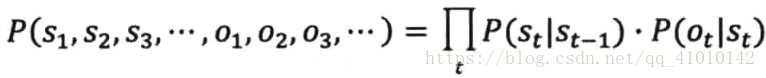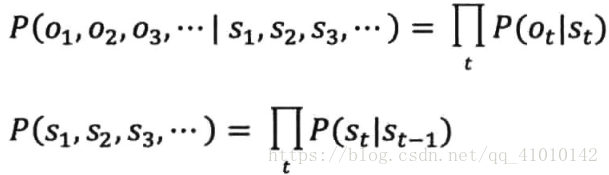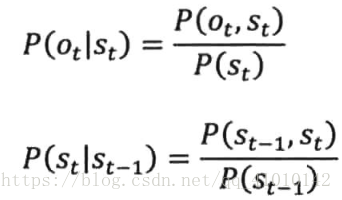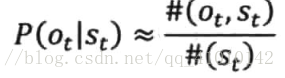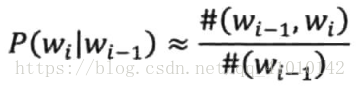《数学之美》——第五章 个人笔记

Posted 2020-11-01 方玲是个小可爱

第五章     隐含马尔可夫模型

1 通信模型

通信的本质是一个编解码和传输的过程。

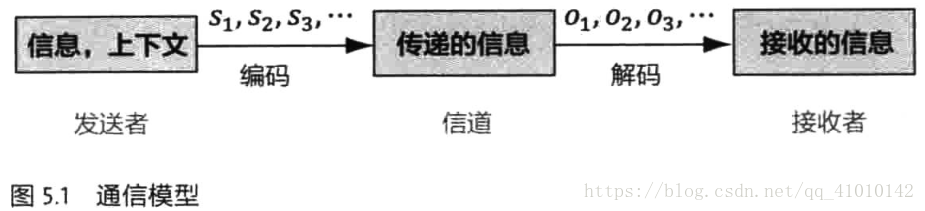
典型的通信系统：

包含雅格布森通信的六个要素：发送者（信息源），信道，接收者，信息，上下文和编码。

其中S1,S2,S3，... 表示信息源发出的信号，比如手机。O1,O2,O3，...是接收器接收到的信号。通信中的解码就是根据接收到的信号O1,O2,O3,...还原出发送的信号S1,S2,S3,...。

在通信中，如何实现上面的解码呢？只需要从所有的源信号中找到最可能产生出观测信号的那一个信息。

用概率论表述：就是在已知O1,O2,O3,...的情况下，求得令条件概率P(S1,S2,S3,...丨O1,O2,O3,...)达到最大值的那个信息串S1,S2,S3,...,即

利用贝叶斯将上式变成：

分子第一个表示信息S1,S2,S3,...在传输后变成接收信号O1,O2,O3,...的可能性；第二个表示S1,S2,S3,...本身是一个在接收端正常的信号的可能性；分母表示发送端产生信息O1,O2,O3,...的可能性。其中，P(O1,O2,O3,...)是可以忽略的常数。等价于求分子：

分子可以用隐含马尔可夫模型来估计

 

 

2 隐含马尔可夫模型

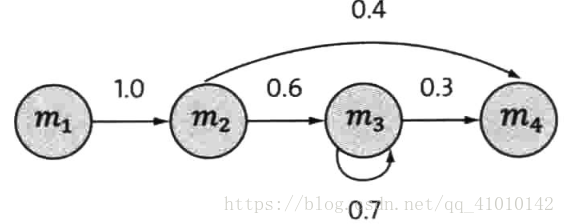
一个离散的马尔可夫过程：

四个圈表示四个状态，每条边表示一个可能的状态转换，边上的权值是转移概率。文中有具体解释

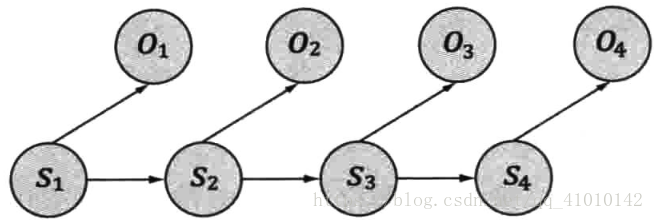
隐含马尔可夫模型是上述马尔可夫链的一个扩展：任一时刻 t 的状态St是不可见的。所以无法通过观察到一个状态序列S1,S2,S3,...,ST来推测转移概率等参数。但是，在每个时刻 t 会输出一个符号Ot ，而且Ot 跟St 相关且仅跟St 相关。这个被称为独立输出假设。

隐含马尔可夫模型的结构如下：

基于上述内容，我们可以计算出某个特定的状态序列S1,S2,S3,...产生出输出符号O1,O2,O3,...的概率。

该式子与上面式子（上面那个分子）相似。把马尔可夫假设和独立输出假设用于通信的解码问题（上面的那个分子）

就是把

 

带入分子，可以等到上式。PS：等号右边第一个概率相当于分子的第二个概率，而第二个概率相当于分子的第一个概率。

 

 

3 延伸阅读：隐含马尔可夫模型的训练

该模型有三个基本问题：

①给定一个模型，如何计算某个特定的输出序列的概率。（Forward-Backward算法）

②给定一个模型和某个特定的输出序列，如何找到最可能产生这个输出的状态序列。（维特比算法）

③给定足够量的观测数据，如何估计隐含马尔可夫模型的参数。（接下里讨论的问题）

实际中，首先要知道P(St丨St-1),也就是转移概率，和P(Ot丨St)，也称为生成概率。这些概率被称为隐含马尔可夫模型的参数，

计算或估计这些参数的过程称为模型的训练。

从条件概率出发：

对于状态输出概率，如果有足够多人工标记的数据，知道经过状态St有多少次#(St),每次经过这个状态时，分别产生的输出Ot是什么，而且分别有多少次#(Ot,St)就可以用两者的比值

直接估算出模型的参数。因为数据是人工标注的，因此这种方法被称为有监督的训练方法。

对于转移概率，和前面提到的训练统计语言模型的条件概率是完全相同的，因此依照

有监督的训练的前提是需要大量人工标注的数据。很多应用无法做到

因此，训练马尔可夫模型更实用的方法是仅仅通过大量观测到的信号O1,O2,O3,...就能推算模型的参数P(St丨St-1)和P(Ot丨St)    的方法，这类方法称为无监督的训练方法。其中主要使用的是鲍姆-韦尔奇算法（Baum-Welch Algorithm）

文中具体对鲍姆-韦尔奇算法做了说明。

鲍姆-韦尔奇算法每一次迭代都是不断地估计新的模型参数，使得输出的概率（目标函数）达到最大化，因此这个过程被称为期望值最大化（Expectation-Maximiztion）,简称EM过程。

EM过程保证一定能收敛到一个局部最优点，但全局却不是。（目标函数是凸函数则可以）