数据结构设计——农夫过河问题

Posted 2020-10-31 醉风晨

本篇文章中所有数据结构都是后期整理的，如有问题欢迎指正，转载请注明出处http://www.cnblogs.com/a1982467767/p/8889683.html

农夫过河问题

 

1、 问题描述：

 

设有一个农夫带一只狼,一只羊和一筐菜来到河边,打算乘一只船从右岸渡到左岸去.该船的负载能力为农夫每次只能带一样东西过河.在无农夫的时候,狼和羊不能在一起,羊和菜不能在一起.设计一个方案,使农夫可以无损失地渡过河.

 

2、 设计思路：

 

设计好图的结构，点以（农夫，狼，羊，菜）表示，设置图的点集，边集，点数，边数；

 

用is_safe函数确定图中各点是否安全，将不安全的点去掉，剩下安全的点，然后判断两点之间是否可变换，再通过层次遍历找到路径，设定好参数，打印出路径；

 

3、 代码实现：

 

  1 #include<stdio.h>
  2 #include<stdlib.h>
  3 #include<windows.h>
  4 #define MaxVertexNum 16
  5 
  6 typedef struct{ 
  7     int farmer;
  8     int wolf;
  9     int sheep;
 10     int vegetable;
 11 }VertexType;//四元组
 12 
 13 typedef struct{
 14     VertexType vertexs[MaxVertexNum];//顶点表表示点集
 15     int edges[MaxVertexNum][MaxVertexNum];//以邻接矩阵表示边集
 16     int vertexNum, edgeNum;//点数，边数
 17 }MGraph;//是以邻接矩阵存储的图类型
 18 
 19 typedef enum{False,Ture} Boolean;
 20 
 21 Boolean visited[MaxVertexNum];//对已经访问的点进行标记
 22 int path[MaxVertexNum];//保存DFS搜索的路径，即某顶点到下一个顶点的路径
 23 
 24 int Locate(MGraph * G, int F, int W, int S, int V)
 25 {
 26     //查找顶点（F,W,S,V）在顶点向量中的位置
 27     int i;
 28     for (i = 0; i < G->vertexNum; i++)
 29         if (G->vertexs[i].farmer == F &&  G->vertexs[i].wolf == W &&
 30             G->vertexs[i].sheep == S && G->vertexs[i].vegetable == V)
 31             return (i);//返回当前位置
 32     return -1;//没有查找到此顶点
 33 }
 34 int Is_safe(int F, int W, int S, int V)
 35 {//当农夫与羊不在一起时，狼和羊 或 羊和白菜在一起是不安全的
 36     if (F != S && (W == S || S == V)) return 0;
 37     else return 1;//否则返回安全
 38 }
 39 
 40 //状态是否可转换，条件是农夫状态不同，物品至多一项不同
 41 int Is_connected(MGraph *G, int i, int j)
 42 {//判断i和j的状态是否可以转换
 43     int k = 0;
 44     if (G->vertexs[i].wolf != G->vertexs[j].wolf) k++;
 45     if (G->vertexs[i].sheep != G->vertexs[j].sheep) k++;
 46     if (G->vertexs[i].vegetable != G->vertexs[j].vegetable) k++;
 47     if (G->vertexs[i].farmer != G->vertexs[j].farmer && k <= 1)
 48         //以上三个条件不同时满足且农夫状态改变时，返回真，即农夫每次只能带一件东西过河
 49         return 1;
 50     else return 0;
 51 }
 52 
 53 void  CreateG(MGraph *G)
 54 {
 55     int i, j, F, W, S, V;
 56     i = 0;
 57     for (F = 0; F <= 1; F++)           //通过安全监测函数，生成所有安全图的顶点
 58         for (W = 0; W <= 1; W++)
 59             for (S = 0; S <= 1;S++)
 60                 for (V = 0; V <= 1;V++)
 61                     if (Is_safe(F, W, S, V))
 62                     {
 63                         G->vertexs[i].farmer = F;
 64                         G->vertexs[i].wolf = W;
 65                         G->vertexs[i].sheep = S;
 66                         G->vertexs[i].vegetable = V;
 67                         i++;
 68                     }
 69     G->vertexNum = i;//安全点数
 70     for (i = 0; i < G->vertexNum; i++)
 71         for (j = 0; j < G->vertexNum; j++)
 72             if (Is_connected(G, i, j))//状态i与状态j之间可转化，初始值为1，否则为0
 73                 G->edges[i][j] = G->edges[j][i] = 1;
 74             else
 75                 G->edges[i][j] = G->edges[j][i] = 0;
 76     return;
 77 }
 78 void Print_Path(MGraph *G, int u, int v)
 79 //输出从u到v的简单路径，即顶点序列中不重复出现的路径
 80 {
 81     int    k;
 82     k = u;
 83     printf("显示右岸已经过河的物体（农夫，狼，羊，菜）\\n");
 84     while (k != v)//可达的情况下，以状态是否相同为依据，打印到达前的所有状态
 85     {
 86         printf("(%d,%d,%d,%d)\\n", G->vertexs[k].farmer, G->vertexs[k].wolf,
 87             G->vertexs[k].sheep, G->vertexs[k].vegetable);
 88         k = path[k];
 89     }
 90     //打印到达的状态
 91     printf("(%d,%d,%d,%d)\\n", G->vertexs[k].farmer, G->vertexs[k].wolf,
 92         G->vertexs[k].sheep, G->vertexs[k].vegetable);
 93 }
 94 
 95 void Print_Graph(MGraph *G, int u, int v)
 96 {//输出从u到v的简单可视
 97     int    k;
 98     k = u;
 99     while (k != v)
100     {    
101         Sleep(1500);
102         system("cls");
103         printf("左岸 ||        || 右岸\\n");
104         printf("-----++--------++-----\\n");
105         if (G->vertexs[k].farmer == 0)    printf("农夫 ||        || \\n");
106         else printf("     ||        || 农夫\\n");
107         if (G->vertexs[k].wolf == 0)    printf(" 狼  ||   河   || \\n");
108         else printf("     ||   河   ||  狼\\n");
109         if (G->vertexs[k].sheep == 0)    printf(" 羊  ||        || \\n");
110         else printf("     ||        ||  羊\\n");
111         if (G->vertexs[k].vegetable == 0)    printf("蔬菜 ||        || \\n");
112         else printf("     ||        || 蔬菜\\n");
113         k = path[k];    
114     }
115     Sleep(1500);
116     system("cls");    
117     printf("左岸 ||        || 右岸\\n");
118     printf("-----++--------++-----\\n");
119     printf("     ||        || 农夫\\n");
120     printf("     ||   河   ||  狼\\n");
121     printf("     ||        ||  羊\\n");
122     printf("     ||        || 蔬菜\\n");
123     printf("农夫的物品已安全过河...\\n");
124 }
125 void DFS_path(MGraph *G, int u, int v)
126 //深度优先搜索从u到v的简单路径
127 {
128     int j;
129     visited[u] = Ture;//标志已访问的顶点，即1
130     for (j = 0; j < G->vertexNum;j++)
131         if (G->edges[u][j] && !visited[j] && !visited[v])
132         {
133             //邻接矩阵中存在u、j两点的路径，且j、v没有被访问
134             path[u] = j;
135             DFS_path(G, j, v);
136         }
137 }
138 int main()
139 {
140     int i, j;
141     MGraph graph;
142     CreateG(&graph);
143     for (i = 0; i < graph.edgeNum; i++)   visited[i] = False;//0表示没有访问，即置初值
144     i = Locate(&graph, 0, 0, 0, 0);//定位i在图存储中的位置
145     j = Locate(&graph, 1, 1, 1, 1);//定位j在图存储中的位置
146     DFS_path(&graph, i, j);
147     if (visited[j])
148     {
149         Print_Path(&graph, i, j);
150         printf("1.5秒后打印路径...\\n");
151         Print_Graph(&graph, i, j);
152 
153     }
154     system("pause");
155     return 0;
156 }

1、 实验结果：

 

........

 

 

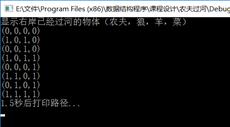
5、  心得体会：

通过两周的课程设计，我学会了如何写一个精简、快速、健壮的程序。一个好的程序应该是一个所占空间小、运行时间短、其他性能也好的程序。而要做出一个好的程序则应该通过对算法与其数据结构的时间复杂度和空间复杂度进行实现与改进。然而，实际上很难做到十全十美，原因是各要求有时相互抵触，要节约算法的执行时间往往要以牺牲更多的存储空间为代价：而为了节省存储空间又可能要以更多的时间为代价。因此，只能根据具体情况有所侧重：如果程序的使用次数较少，则应该力求算法简明易懂，而易于转换为上机程序；如果程序反复多次使用，则应该尽可能选用快速算法；如果解决问题的数据量极大，机器的内存空间较小，则在编写算法时应该考虑如何节省空间。  本次课程设计培养了了我们独立思考的能力，提高了我们的动手操作水平。在具体设计操作中，我们巩固了本学期所学的数据结构与算法的理论知识，进一步提高了自己的编程能力。这也是课程设计的最终目的所在。通过实际操作，开发了自己的逻辑思维能力，培养了分析问题、解决问题的能力。  但在程序设计的过程中我也深刻的感受到自己实力的不足，无法灵活的运用各种工具和函数，对于课程所讲的东西也无法在脱离课本的情况中完成，我意识到自己在今后的学习生活中，一定要勤于思考，扎实掌握理论知识，灵活运用课上所学的东西，做一个优秀的程序员。