LA3487最小割-经典模型 两种方法
Posted Konjak谷弱
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LA3487最小割-经典模型 两种方法相关的知识,希望对你有一定的参考价值。
题意:A、B两个公司要买一些资源(他们自己买的资源不会重复),一个资源只能卖给一个公司。问最大收益。
simple input 部分:
54 1 //买到1就给54元
15 2
33 3
2 4 5//买到4、5就给2元
题解:这道题是很经典的模型题,在这里给出两个方法。
方法一 把每个询问看成一个点,然后A的询问连源点,B的询问连汇点,如果AB间的某个询问有矛盾就在它们中间连一条无限大的边,ans=sum-最小割。

// 方法一 把每个询问看成一个点,然后A的询问连源点,B的询问连汇点,如果AB间的某个 // 询问有矛盾就在它们中间连一条无限大的边,ans=sum-最小割。 #include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<queue> #include<vector> using namespace std; const int N=300100,INF=(int)1e9; int s,t,len,num; int first[2*N],dis[2*N]; int A[N],B[N],p1[N],p2[N]; // bool vis[2*N]; bool vis[3100][3100]; struct node{ int x,y,d,next; }a[6*N]; queue<int> q; int minn(int x,int y){return x<y ? x:y;} int maxx(int x,int y){return x>y ? x:y;} void ins(int x,int y,int d) { a[++len].x=x;a[len].y=y;a[len].d=d; a[len].next=first[x];first[x]=len; a[++len].x=y;a[len].y=x;a[len].d=0; a[len].next=first[y];first[y]=len; } bool bfs(int st,int ed) { while(!q.empty()) q.pop(); memset(dis,-1,sizeof(dis)); dis[st]=0; q.push(st); while(!q.empty()) { int x=q.front();q.pop(); for(int i=first[x];i!=-1;i=a[i].next) { int y=a[i].y; if(dis[y]==-1 && a[i].d>0) { dis[y]=dis[x]+1; q.push(y); } } } return (dis[ed]!=-1); } int dfs(int x,int ed,int flow) { int r=0,p; if(x==ed) return flow; for(int i=first[x];i!=-1;i=a[i].next) { int y=a[i].y; if(dis[y]==dis[x]+1 && a[i].d>0) { p=minn(a[i].d,flow-r); p=dfs(y,ed,p); r+=p; a[i].d-=p; a[i^1].d+=p; } } if(!r) dis[x]=-1; return r; } int dinic(int st,int ed) { int ans=0; while(bfs(st,ed)) { int p; while(p=dfs(st,ed,INF)) ans+=p; } return ans; } int main() { int T,cas=0; scanf("%d",&T); while(T--) { len=-1; memset(first,-1,sizeof(first)); memset(A,0,sizeof(A)); memset(B,0,sizeof(B)); memset(vis,0,sizeof(vis)); int n,m,sum=0,mx=0,num=300001; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&p1[i]); sum+=p1[i]; int x;num++; while(1) { char c; scanf("%d%c",&x,&c); A[x]=i; mx=maxx(mx,x); if(c==\'\\n\') break; } } scanf("%d",&m); s=0,t=n+m+1; for(int i=1;i<=m;i++) { scanf("%d",&p2[i]); sum+=p2[i];num++; int x; while(1) { char c; scanf("%d%c",&x,&c); B[x]=i; mx=maxx(mx,x); if(c==\'\\n\') break; } } for(int i=1;i<=n;i++) ins(s,i,p1[i]); for(int i=1;i<=m;i++) ins(i+n,t,p2[i]); for(int i=1;i<=mx;i++) { if(!A[i]||!B[i]||vis[A[i]][B[i]]) continue; vis[A[i]][B[i]]=true; ins(A[i],B[i]+n,INF); } printf("Case %d:\\n",++cas); printf("%d\\n",sum-dinic(s,t)); if(T) printf("\\n"); } return 0; }
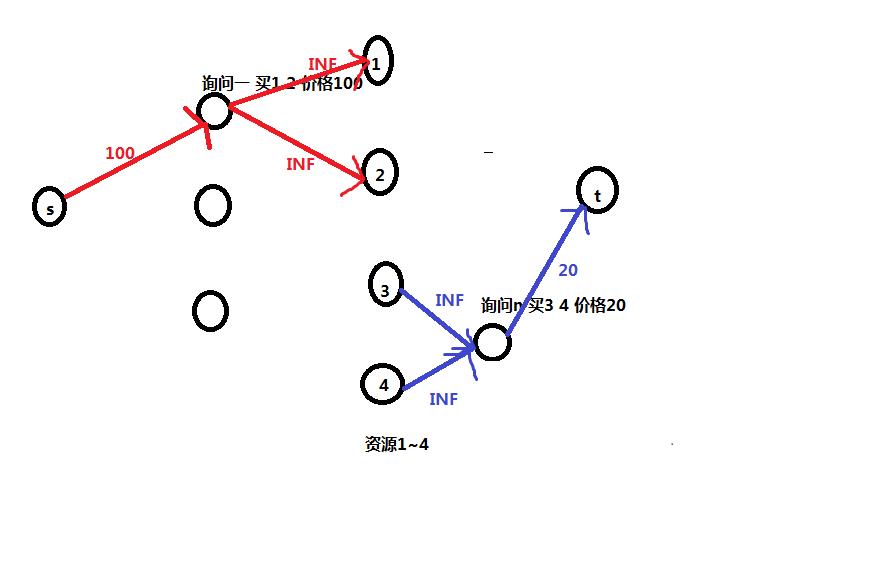
方法二:对于每个询问,新建一个点x,如果是A就源点连向这个点,流量为价钱p,然后x连向这个询问所要求买的资源c[i],流量为INF。
如果是B则反过来,连向汇点。

#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<queue> #include<vector> using namespace std; const int N=300100,INF=(int)1e9; int s,t,len,num; int first[2*N],dis[2*N]; int A[N],B[N]; bool vis[3100][3100]; struct node{ int x,y,d,next; }a[6*N]; queue<int> q; int minn(int x,int y){return x<y ? x:y;} int maxx(int x,int y){return x>y ? x:y;} void ins(int x,int y,int d) { a[++len].x=x;a[len].y=y;a[len].d=d; a[len].next=first[x];first[x]=len; a[++len].x=y;a[len].y=x;a[len].d=0; a[len].next=first[y];first[y]=len; } bool bfs(int st,int ed) { while(!q.empty()) q.pop(); memset(dis,-1,sizeof(dis)); dis[st]=0; q.push(st); while(!q.empty()) { int x=q.front();q.pop(); for(int i=first[x];i!=-1;i=a[i].next) { int y=a[i].y; if(dis[y]==-1 && a[i].d>0) { dis[y]=dis[x]+1; q.push(y); } } } return (dis[ed]!=-1); } int dfs(int x,int ed,int flow) { int r=0,p; if(x==ed) return flow; for(int i=first[x];i!=-1;i=a[i].next) { int y=a[i].y; if(dis[y]==dis[x]+1 && a[i].d>0) { p=minn(a[i].d,flow-r); p=dfs(y,ed,p); r+=p; a[i].d-=p; a[i^1].d+=p; } } if(!r) dis[x]=-1; return r; } int dinic(int st,int ed) { int ans=0; while(bfs(st,ed)) { int p; while(p=dfs(st,ed,INF)) ans+=p; } return ans; } int main() { int T,cas=0; scanf("%d",&T); while(T--) { len=-1; memset(first,-1,sizeof(first)); memset(A,0,sizeof(A)); memset(B,0,sizeof(B)); memset(vis,0,sizeof(vis)); int n,m,p,sum=0,mx=0,num=300001; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&p); sum+=p; int x;num++; ins(0,num,p); while(1) { char c; scanf("%d%c",&x,&c); ins(num,x+1,INF); if(c==\'\\n\') break; } } scanf("%d",&m); s=0,t=1; for(int i=1;i<=m;i++) { scanf("%d",&p); sum+=p;num++; ins(num,t,p); int x; while(1) { char c; scanf("%d%c",&x,&c); ins(x+1,num,INF); if(c==\'\\n\') break; } } for(int i=1;i<=n;i++) ins(s,i,p1[i]); for(int i=1;i<=m;i++) ins(i+n,t,p2[i]); for(int i=1;i<=mx;i++) { if(!A[i]||!B[i]||vis[A[i]][B[i]]) continue; vis[A[i]][B[i]]=true; ins(A[i],B[i]+n,INF); } printf("Case %d:\\n",++cas); printf("%d\\n",sum-dinic(s,t)); if(T) printf("\\n"); } return 0; }
以上是关于LA3487最小割-经典模型 两种方法的主要内容,如果未能解决你的问题,请参考以下文章
UVALive - 3487 Duopoly(网络流-最小割)
