算法均匀的生成圆内的随机点

Posted 2020-10-31 Vincent丶

 

算法 1

设半径为$R$。

$x = r \\ast cos(\\theta)$

$y = r \\ast sin(\\theta)$

其中 $0\\leqslant r \\leqslant R$，$t$为0-1均匀分布产生的随机数，$r = sqrt(t) \\ast R$，$\\theta = 2\\pi \\ast t, t \\sim U(0, 1)$ 证明：url

 1 import numpy as np
 2 import random
 3 import math
 4 import matplotlib.pyplot as plt
 5 import matplotlib as mpl
 6 mpl.rcParams[\'agg.path.chunksize\'] = 10000 # the default is 0
 7 N = int(10000)
 8 x1 = 1.5
 9 x2 = 0.5
10 radius = 2
11 a = 2 * math.pi * np.array([random.random() for _ in range(N)])
12 r = np.array([random.random() for _ in range(N)])
13 x = radius*np.sqrt(r)*np.cos(a) + x1;
14 y = radius*np.sqrt(r)*np.sin(a) + x2;
15 plt.scatter(x, y, s=1)
16 plt.show()

 

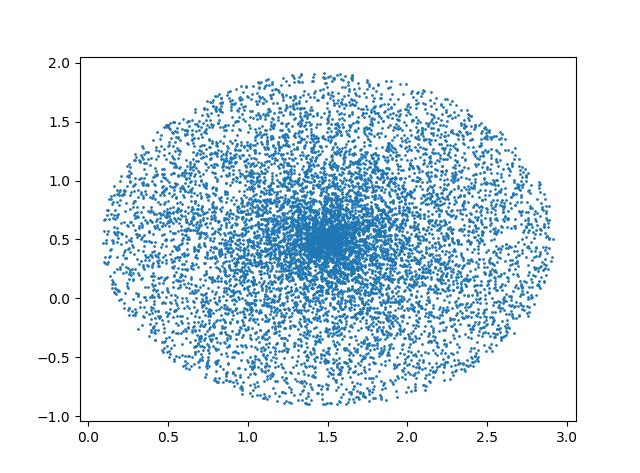
下面的算法是错误的

原因在于对$R$求开方，导致$r = sqrt(R)*t$平方后不在满足均匀分布。

 1 import numpy as np
 2 import random
 3 import math
 4 import matplotlib.pyplot as plt
 5 import matplotlib as mpl
 6 mpl.rcParams[\'agg.path.chunksize\'] = 10000 # the default is 0
 7 N = int(10000)
 8 x1 = 1.5
 9 x2 = 0.5
10 radius = 2
11 a = 2 * math.pi * np.array([random.random() for _ in range(N)])
12 r = np.array([random.random() for _ in range(N)])
13 #x = radius*np.sqrt(r)*np.cos(a) + x1;
14 #y = radius*np.sqrt(r)*np.sin(a) + x2;
15 x = np.sqrt(radius)*r*np.cos(a) + x1;
16 y = np.sqrt(radius)*r*np.sin(a) + x2;
17 plt.scatter(x, y, s=1)
18 plt.show()

 参考链接：JustDoIT