吴恩达机器学习笔记-第四周

Posted 2020-10-31 jiangxinyang

 

八、神经网络：表述

8.1 非线性假设

为什么需要提出神经网络，当我们在用逻辑回归或者线性回归处理分类问题时，当特征的数量较少时我们可以很好的处理，但是当特征的数量很大时，比如特征的数量为n，而很多时候我们的这些特征可能还会组合在一起形成新的特征，例如每个都两两组合就会有n²/2，而如果考虑多个组合在一起的时候，则特征量会非常大，此时若仍然采用逻辑回归的计算量会非常大。

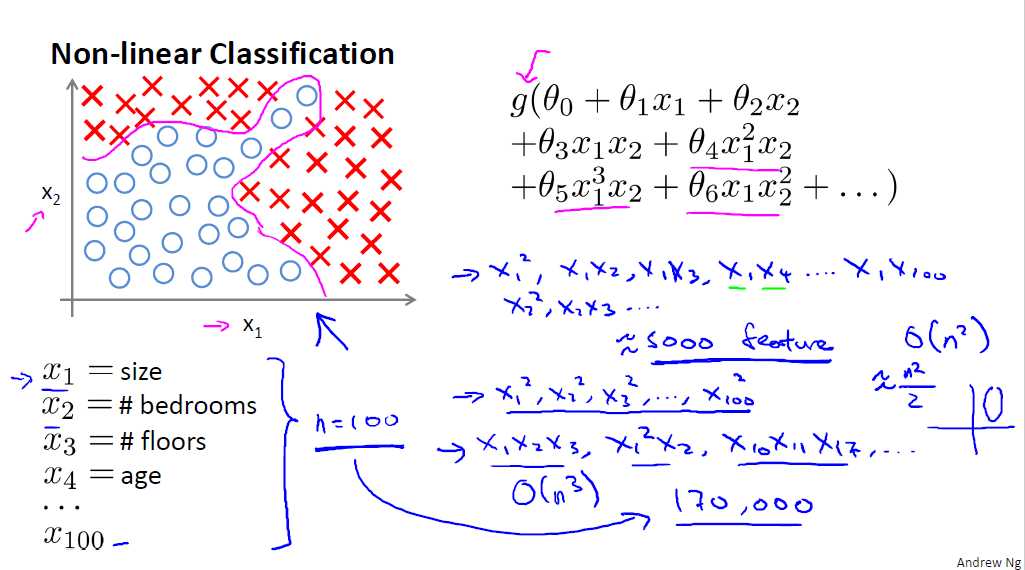
一般来说为了很好的拟合，很多时候都需要采用非线性分类（多次多项式都属于非线性），当特征很少时，可以很好的用逻辑回归处理， 而如上图所示当特征很多的时候，我们就需要借助接下来的神经网络来解决问题了。

8.2 神经元和大脑

略

8.3 模型表示1

 接下来我们看看简单的神经网络模型

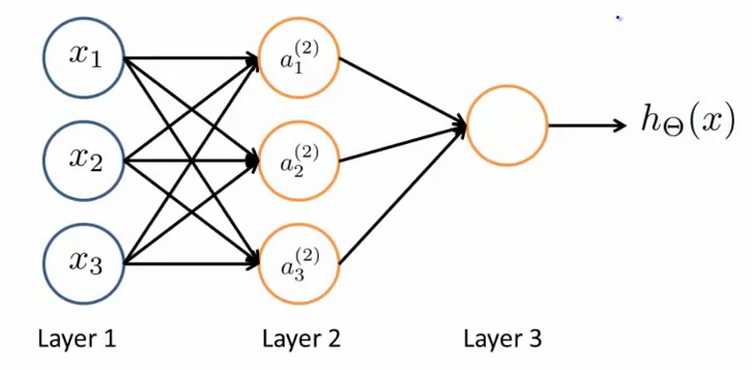
在这里x1，x2，x3是输入单元，我们将原始数据输入到输入单元中，a1，a2，a3表示中间单元(其中括号中的2表示是第二层，我们通常将输入单元看作第一层，输出单元看作最后一层)，他们负责将输入的数据进行处理并将处理的结果返回到下一层，最后一层是输出单元，他负责计算hΘ(x)的结果。

神经网络模型的本质就是许多逻辑单元按照不同你层级组织起来的网络，每一层的输出变量都是下一层的输入变量，一般将第一层成为输入层，最后一层成为输出层，而中间的层都成为隐藏层。我们为每一层添加一个偏差单元（其实就是常数项中的x0，在之前的逻辑回归中就是θ0×x0这一项），则可以表示为如下图

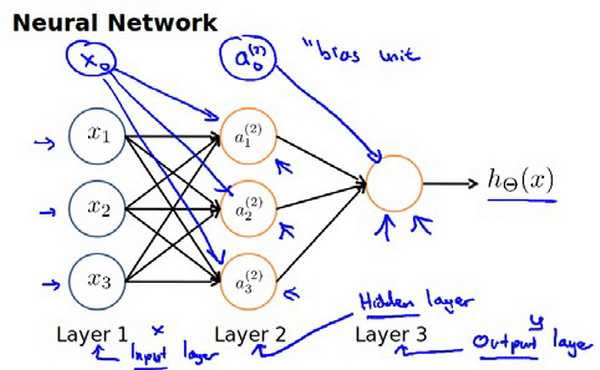
从上图中的连接线可以看出，一个θTX只会输出一个激活单元（激活单元即上面的a1之类的），而在一个层中会有多个激活单元（如a2，a3），那么从上一层往下一层的转化也就需要多个θ，在这里我们可以将这些θ组合成一个矩阵。以θ^(j)为例，在这里θ^(j)表示从第j层到第j+1层的映射权重矩阵，则该矩阵的行数为j+1层的激活单元个数，而列数则为第j层的激活单元个数（在这里结合之前的逻辑回归，第j层的激活单元个数可以看做是特征的个数），a_i^(j)就代表第j层的第i各激活单元。

对于上图中的模型，第二层的激活单元和输出层的表达式可以写成：

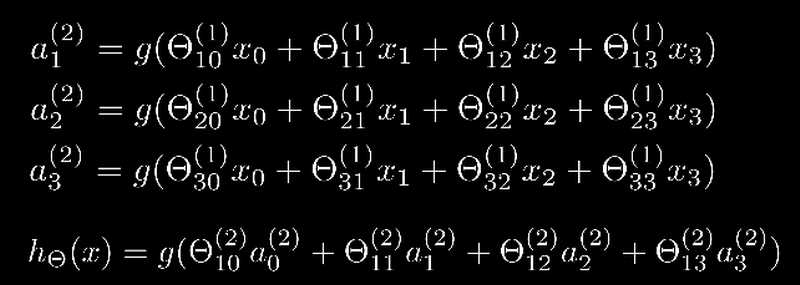
在上图中的Θ₁₀⁽¹⁾的数字含义是(1)表示这是第一层的权重参数Θ，而10表示的是行数和列数，1表示第一行(第一行权重参数对应的输出值是第一份激活单元)，0表示第0列(为什么会有第0列，这是我们引入的偏差单元对应的Θ0，也会对应着x向量中的第0各元素)。

在上面我们都只是讨论了一个数据点X，得到的a1，a2...都只是一个数值，而往往我们都是将一个数据集D入到到模型中，因此我们输入的X不再是一个向量，而是一个矩阵(矩阵的行为数据点的个数，列为特征的数量)，因此输出的a1，a2...不再是一个数值，而是一个向量，组合在一起也就是一个矩阵。矩阵中的每一个a都是由上一层对应行的所有x的值和x对应的权重θ所决定的。我们把这种从左到右的算法称为前向传播算法。

把x，θ和a分别用矩阵表示：我们可以得到a=θ.x，因此神经网络的传播过程中可以看做矩阵和矩阵相乘。

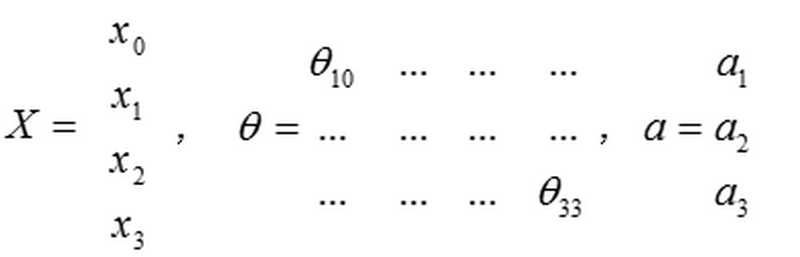
8.4 模型表示2

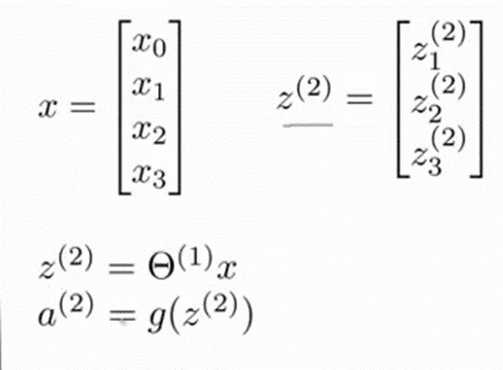
起始神经网络之间的传递和逻辑回归很相似，都是引入一个函数g(x)来处理θ^Tx，然后输出值

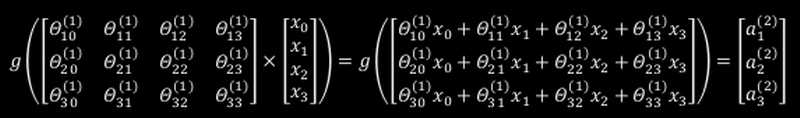
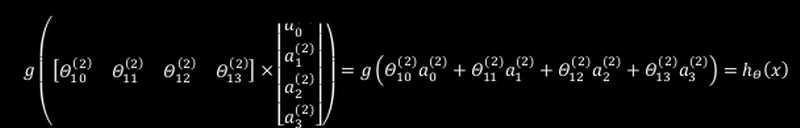
如上所示a_i⁽²⁾=g(z⁽²⁾)，z⁽²⁾ = θ_i⁽¹⁾x，这种运算方式和逻辑回归非常相似，只是逻辑回归中的g(x)确定是sigmod函数(其实在这里我们的g(x)也可以用sigmod函数，而且每次输出的值都在[0, 1]范围内，这样在作为下个输入值时还不需要做归一化处理)。

而在最后一层的输入输出时，就可以看做成逻辑回归，唯一的区别是输入值不再是x，而是a，而a可是是从x中按照梯度下降变化出来的，因此a可以看做是更高级的特征值，这些值比x的高阶值能更好的预测新数据。

8.5 特征和直观理解

接下来我们先用神经网络表示与，或，非函数

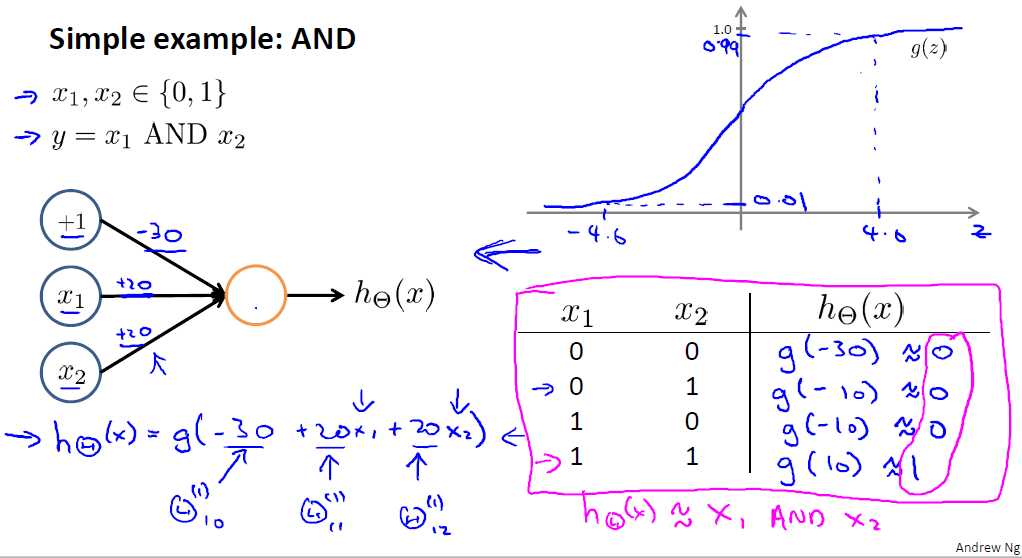
与函数

或函数

 

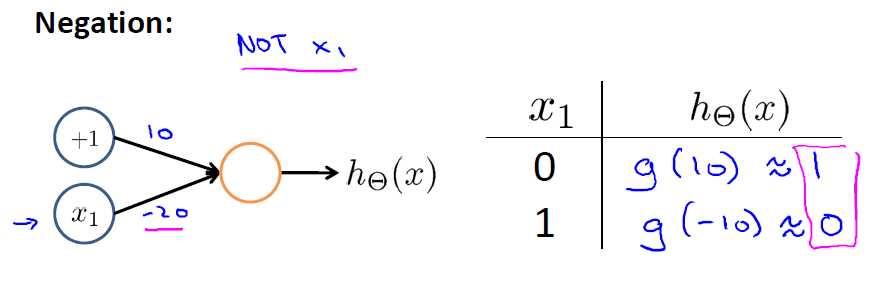
 非函数

可以看到实现与、或、非函数只要用两层神经网络就可以实现，或者说是用逻辑回归的方法就可以实现，但是当我们要实现异或函数的时候就没有那么容易实现了，此时需要借助多层神经网络

异或可以拆分成与、或、非的组合形式，x1 XNOR x2 = (x1 AND x2) OR (NOT x1) AND (NOT x2) (按照运算的级别，与的级别高于或)，在这里我们可以理解为将一个复杂的表示式拆分成简单的表示是的组合，例如一个高阶的多项式可以拆分成多个低阶多项式的组合，组合形式可以是加减乘除。

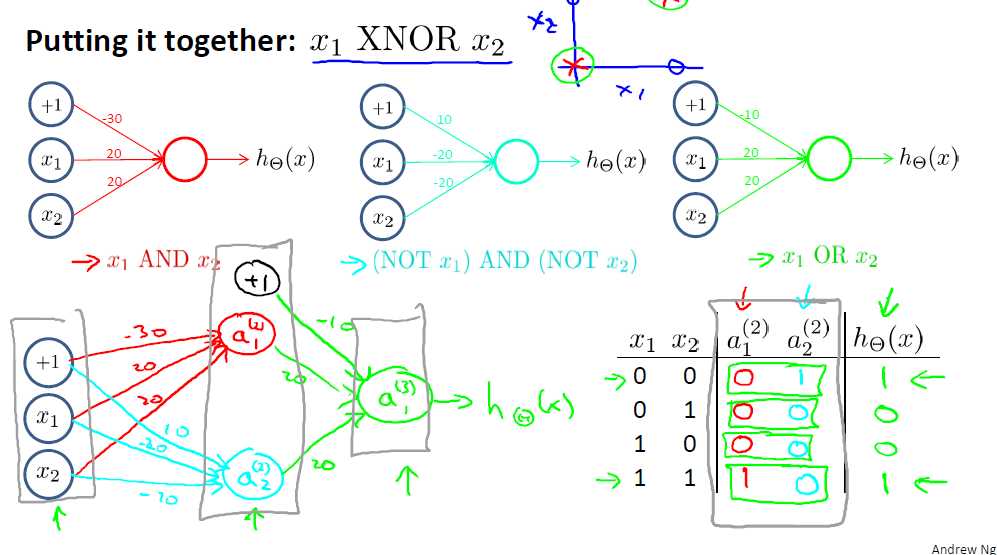
8.6 多类分类

利用神经网络算法处理多分类问题时，输出的不再是一个单一的数值，而是一个向量，但该向量中只有一个值为1，其余的值为0，如下图所示

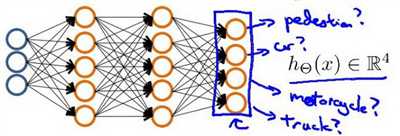
输入的特征数据的特征只有三个，输出的向量中值的个数为所需分类的数量，输出的结果表示如下

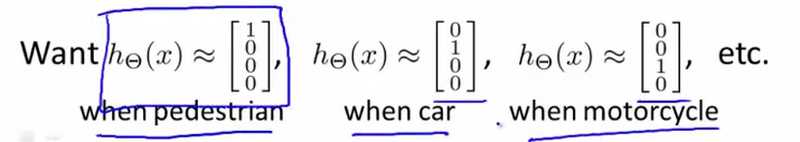
上面神经网络算法输出的可能的值如下四种：