没有上司的舞会（题解）

Posted 2020-10-31 Zhoier

作为人生中的第一道树形DP题，写一篇题解也是很有意义的。

 

没有上司的舞会

题目描述

某大学有N个职员，编号为1~N。他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数Ri，但是呢，如果某个职员的上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

输入输出格式

输入格式：

 

第一行一个整数N。(1<=N<=6000)

接下来N行，第i+1行表示i号职员的快乐指数Ri。(-128<=Ri<=127)

接下来N-1行，每行输入一对整数L,K。表示K是L的直接上司。

最后一行输入0 0

 

输出格式：

 

输出最大的快乐指数。

 

输入样例：

7

1

1

1

1

1

1

1

1 3

2 3

6 4

7 4

4 5

3 5

0 0

 

输出样例：

5

 

我们先来分析一下树形DP是如何工作的：

为了保证树形DP取点完整且最优，我们就必须要以叶节点为起点，以根节点为终点（因为叶节点的区域相比根节点的区域更稠密）。

这题有个不严谨的地方：上司来了，他的职员就不能来，却没说是直接上司还是所有的上司；但是根据个人分析和样例给出的数据来看，应该是直接上司；如果有越级的上司则该职员也可以来（现实也是这样，职员又很小概率认识自己上司的上司的上司的上司……（此处省略n个上司，n∈z））。

然后，本题的每个点的值都是1，按照下面的样例可以组成这样的一棵树（0 0 的点忽略）：

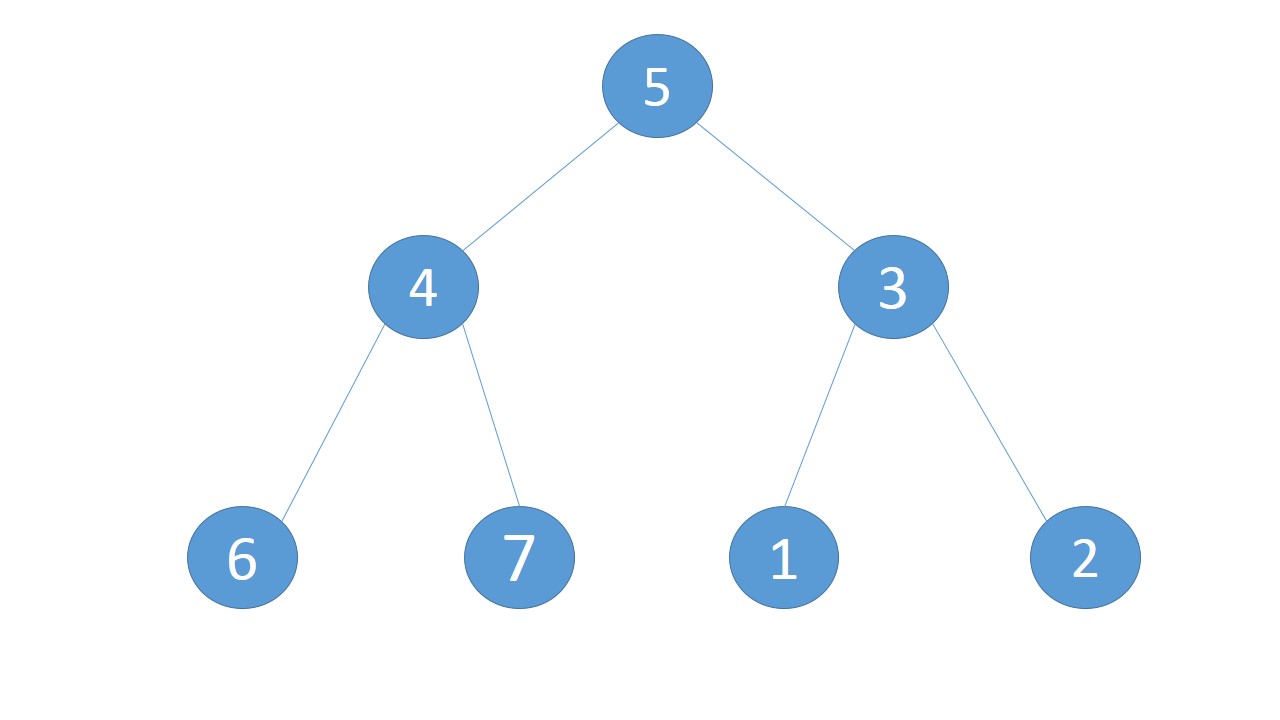
因为如果选了该员工的上司就无法选择这个员工，所以需要vis数组判断改点能否取（他的上司（father）被取了，则所有的职员（son）就不能取）；

但是用vis数组来判断的话，是不是如果上司改了，他的职员就得全部改掉，甚至还要用到并查集来判断哪些点的上司的职员，未免有些太麻烦了（如果你会多叉转二叉，那就呵呵了；但我相信会此算法的神犇是不会来看该博客的o(*￣︶￣*)o）。因此，我们会在dp[]的基础上再开一维，专门用来判断当前这个人去还是不去。！！！注意，vis数组却必须要用的，这里的dp[...][0]或dp[...][1]只代表在状态转移时用来判断取还是不取，相当于一个预处理；实际上你取完之后是要在把他压到队列里的，也就是这个点时实际已经取的，不是用来动态规划用的！！！

设：

dp[x][0]表示以x为根的子树,且x不参加舞会的最大快乐值；

dp[x][1]表示以x为根的子树，且x参加了舞会的最大快乐值。

则dp[x][0] = sigma{max(dp[y][0],dp[y][1])} (y是x的儿子)

dp[x][1] = sigma{dp[y][0]}+happy[x] (y是x的儿子)

以这种方式处理就很好地解决了只判断直接上司的问题了，并且sigma的目的是将改子树的happy值的和算出来，这也是本题所要求的。

 

最后找到唯一的树根root：

zxy(i,1,n)// i = 1 to n
        if(!v[i])
        {
            root = i;
            break;
        }

哎？v[]是什么东西？？：

zxy(i,1,n - 1)
    {
        ll x,y;
        scanf("%lld%lld",&x,&y);
        son[y].push_back(x);
        v[x] = 1;
    }

哦！在读入的时候就把谁是谁的职员压到队列里了，因为根节点就相当于boss，他是没有上司的，所以说它是不会在v[]里的。

找出根节点在进行dp操作，就可以求出最大子树了！

AC代码：

#pragma GCC optimize(2)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <vector>
#include <set>
#include <stack>
using namespace std;
typedef long long ll;
#define N 23333
#define zxy(i,a,b) for(ll i = a ; i <= b ; i++)
#define yxz(i,a,b) for(ll i = a ; i >= b ; i--)
ll f[N][2],happy[N];
ll v[N];
vector <long long> son[N];
ll mymax(ll a,ll b)
{
    return a > b ? a : b;
}
void zhoier(ll x)
{
    f[x][0] = 0;
    f[x][1] = happy[x];
    for(ll i = 0 ; i < son[x].size() ; i++)
    {
        ll y = son[x][i];
        zhoier(y);
        f[x][0] += mymax(f[y][0],f[y][1]);
        f[x][1] += f[y][0];
    }
}
int main()
{
    ll n;
    scanf("%lld",&n);
    zxy(i,1,n)
        scanf("%lld",&happy[i]);
    zxy(i,1,n - 1)
    {
        ll x,y;
        scanf("%lld%lld",&x,&y);
        son[y].push_back(x);
        v[x] = 1;
    }
    ll mei,yong;
    scanf("%lld%lld",&mei,&yong);
    ll root;
    zxy(i,1,n)
        if(!v[i])
        {
            root = i;
            break;
        }
    zhoier(root);
    //printf("1");
    printf("%lld",mymax(f[root][0],f[root][1]));
    return 0;
}