形态学及其他集合运算(Morphological and Other Set Operations)

Posted 2020-10-30 luofeel

摘    要：本实验主要实现形态学图像处理。主要验证图像集合的交并补运算、膨胀和腐蚀处理并利用图像集合的运算，实现形态学边界抽取算法并进行特征边界抽取。同时将膨胀和腐蚀扩展至灰度图像，编写函数实现灰度图像形态学梯度公式和Tophat变换公式，最后对形态学梯度变换和Tophat变换后的输出图像进行比较。

 

1 形态学

 

形态学(motphology)一词通常代表生物学的一个分支。它是研究动物和植物的形态和结构的学科。我们在这里使用同一词语表示数学形态学的内容，将数学形态学(mathenmfical  morphology)作为工具从图像中提取对于表达和描绘区域形状有用处的图像分量，比如边界、骨架以及凸壳，等等。我们对用于预处理或后处理的形态学技术同样感兴趣，比如形态学过滤、细化和修剪等等。

数学形态学的语言是集合论。同样，形态学为大量的图像处理问题提供了一种一致的有力方法。数学形态学中的集合表示图像中的不同对象。例如，在二值图像中，所有黑色像素的集合是图像完整的形态学描述。在二值图像中，正被讨论的集合是二维整数空间 (P)的元素，在这个二维整数空间中，集合的每个元素都是一个多元组(二维向量)，这些多元组的坐标是一个黑色(或白色，取决于事先的约定)像素在图像中的坐标(x,y)。灰度级数字图像可以表示为Z空间(Z3)上分量的集合。在这种情况下，集合中每个元素的两个分量是像素的坐标，第3个分量对应于像素的离散灰度级值。更高维度空间中的集合可以包含图像的其他属性，比如颜色和随时间变化的分量。

2 图像的逻辑运算

 

       很多应用是以形态学概念为基础的，并涉及二值图像。逻辑运算尽管本质上很简单，但对于实现以形态学为基础的图像处理算法是一种有力的补充手段。本实验中，我们关注的是涉及二值图像和灰度图像的逻辑运算。

       在图像处理中用到的主要逻辑运算是：与、或和非(即交并补)。图1中总结了这些运算的性质。这些运算在功能上是完善的。它们可以互相组合形成其他逻辑运算。

图1 主要的逻辑运算

       在两幅或多幅图像的对应像素间逐像素进行逻辑运算(除了“非”运算，此运算只对单一图像的像素进行)。因为只有在两个变量都是1时，两个二进制变量的“与”运算才为1，所以只有两幅输人图像的对应像素均为1时，“与”运算的结果才是1。图2显示了涉及图像逻辑运算的不同例子。这里，黑色表示1，而白色表示0（这里使用两种约定的说法，有时会颠倒黑色和白色二值的意义，取决于在给定情况下哪种表达更清楚。使用图1中的定义构造其他的逻辑运算很容易。例如，异或运算是当两个像素的值不同时结果为1，否则为0。这种运算与“或”运算不同。“或”运算在两个像索有一个为1或两个均为1时结果为1。

图2 图像逻辑运算

3 二值图像膨胀与压缩

 

二值图像膨胀：设A和B是(Z2)中的集合，A被B膨胀定义为：

       这个公式是以得到B的相对于它自身原点的映像并且由z对映像进行位移为基础的。A被占膨胀是所有位移z的集合，这样，B和 A至少有一个元素是重叠的。与在其他形态学运算中一样，集合B通常叫做膨胀的结构函数。

二值图像压缩：对Z中的集合A和B，使用B对A进行腐蚀定义为：

      这个公式说明，使用B对A进行腐蚀是所有B中包含于A中的点z的集合用z平移。

4 形态学边界特征提取

 

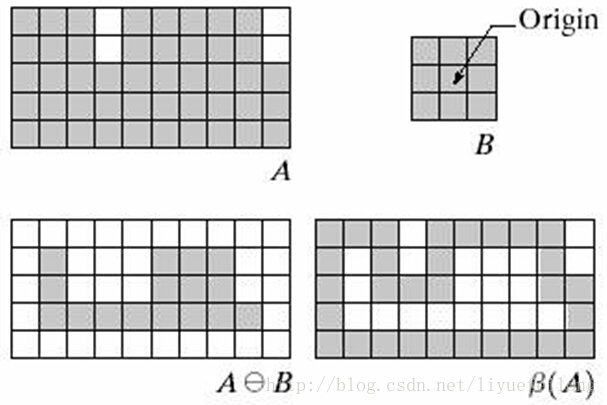
      集合A的边界表示为 ，它可以通过先由B对A腐蚀，而后用A减去腐蚀得到。即：

      这里B是一个适当的结构元素。图3说明了边界提取的机理。这幅图像显示了一个简单的二值对象、一个结构元素B和使用式 的结果。尽管图3中显示的结构元素是最常用的结构元素之一，但它绝对不是惟一的。例如，使用由1组成的5×5大小的结构元素将得到2到3个像素宽的边界。

 

图3 边界提取机理

5 灰度图像扩展——膨胀和腐蚀

 

 

 

         用结构元素B对灰度图像进行膨胀表示为：，定义为：

       这里和分别是f和b的定义域。f和b是函数而不是二值形态学情况中的集合。 必须在f的定义域内以及x和y 必须在b的定义域内的条件与膨胀的二值定义中的条件是相似的(这里两个集合的交集至少应有一个元素)。该公式的形式与二维卷积是相似的，并且用最大值运算代替卷积求和，用加法运算代替卷积乘积。

       用结构元素B对灰度图像进行腐蚀表示为： ，定义为：

       这里和分别是f和b的定义域。平移参数必须在f的定义域内，而且x和y必须在b的定义域内，这与腐蚀的二值定义中的条件相似。同样，公式在形式上与二维相关是相似的，并且用最小值运算代替了相关运算，用减法运算代替了相关的乘积。

6 灰度图像形态学的应用

       膨胀和腐蚀经常用于计算图像的形态学梯度，其公式为：

形态学梯度的作用是使输入图像中灰度级的跃变更为急剧。

      另外一个应用是对图像进行形态学tophat变换，定义为：

      如以前一样，f是输入图像，b是结构元素函数。该应用对于增强灰度图像的阴影细节很有用处。

 

 

7 实验结果讨论

    本实验使用B=ones(3,3)矩阵作为结构元素，使用图像Fig9.20(left).jpg进行二值图像的膨胀、腐蚀和边缘特征提取处理，使用图像Fig9.39(a).jpg实现灰度图像的膨胀、腐蚀并进行形态学梯度公式运算和Tophat变换。

    编写函数dilate_erode(ima,B)实现二值图像的膨胀与腐蚀，其中ima为输入图像，A为结构元素。图4给出了二值图像的膨胀、腐蚀和边缘特征提取等处理结果，可以看到，腐蚀图中消除了一些原图的细节，而膨胀图则相反。由于腐蚀图中主要消除了原图的边缘细节，因此根据边缘特征提取的原理，我们将原图像与腐蚀图像相减，即可得到院图像的边缘部分细节。

    编写函数gray_dilate_erode(ima,B,operate)实现灰度图像的膨胀与腐蚀，其中ima为输入图像，B为结构元素，operate为可选操作膨胀’dilate’和腐蚀’erode’。图5给出了灰度图像的膨胀、腐蚀并与MATLAB自带函数进行对比，结果并无差异。使用公式：

     

    分别实现形态学梯度公式和tophat变换，结果如图6所示。可以看到经过形态学梯度公式处理后的图像中灰度级的跃变更为急剧，边界轮廓明显，但输出图像有明显的噪声；而tophat变换后的输出图像的阴影细节得到增强，其他区域无明显变化。

 

8 实验结果图片