Tree Restoring

Posted 2020-10-30 oc_co

题目描述

Aoki loves numerical sequences and trees.

One day, Takahashi gave him an integer sequence of length N, a1,a2,…,aN, which made him want to construct a tree.

Aoki wants to construct a tree with N vertices numbered 1 through N, such that for each i=1,2,…,N, the distance between vertex i and the farthest vertex from it is ai, assuming that the length of each edge is 1.

Determine whether such a tree exists.

Constraints
2≤N≤100
1≤ai≤N−1

输入

The input is given from Standard Input in the following format:
N
a1 a2 … aN

输出

If there exists a tree that satisfies the condition, print \'Possible\'. Otherwise, print \'Impossible\'.

样例输入

5
3 2 2 3 3

样例输出

Possible

提示

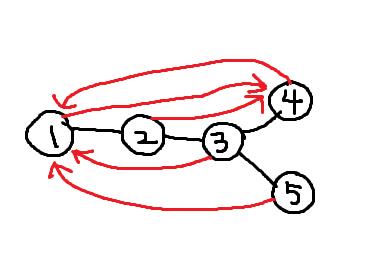
The diagram above shows an example of a tree that satisfies the conditions. The red arrows show paths from each vertex to the farthest vertex from it.

 解析

代码比较长，整体思路就是先排序，找到最长的那一路，然后确定这个长度为主干（比如说最长的是n，那主干长度是n+1），然后把其他的分支都可以插在中间，但是这些分路构成的长度不能长于主干长度，因此这些分支的距离就是主干中间的最长距离加一，就比如说样例，主干长度是3，因此有4个数为主干，因此这四个数的最长距离为3、2、2、3，剩下的一个可以在中间的两个二中任选一个加一，就是3、2、2、3、3。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int s[200];
int main()
{
 
    ios::sync_with_stdio(false);
    int i,j,k,m,n;
    int ans=0,cnt=0;
    int flag=0;
    int flag1=0;
    cin>>n;
    for(i=1; i<=n; i++) cin>>s[i];
    sort(s+1,s+n+1);
    int gen=s[n],num=0;
    for(i=1; i<=n; i++)
        if(s[i]==gen) num++;
    if(num==1) cout<<"Impossible"<<endl;
    else
    {
        if(gen%2!=0)
        {
 
            k=(gen+1)/2;
            m=k;
            for(i=1;i<=n;i++)
            {
                if(s[i]==k)
                {
                    cnt++;
                }
                if(cnt>2)
                {
                    cout<<"Impossible"<<endl;
                    return 0;
                }
            }
            for(i=1; i<=n; i++)
            {
                if(s[i]<k)
                {
                    cout<<"Impossible"<<endl;
                    return 0;
                }
                if(m==s[i])
                {
                    ans++;
                }
                if(ans==2)
                {
                    ans=0;
                    m++;
                }
                if(m==(gen+1))
                {
                    cout<<"Possible"<<endl;
                    return 0;
                }
            }
            cout<<"Impossible"<<endl;
        }
        else
        {
            k=gen/2;
            m=k;
             for(i=1;i<=n;i++)
            {
                if(s[i]==k)
                {
                    cnt++;
                }
                if(cnt>1)
                {
                    cout<<"Impossible"<<endl;
                    return 0;
                }
            }
            for(i=1; i<=n; i++)
            {
                if(s[i]<k)
                {
                    cout<<"Impossible"<<endl;
                    return 0;
                }
 
                if(m==s[i])
                {
                    ans++;
                }
                if(ans==2&&flag)
                {
                    ans=0;
                    m++;
                }
                else if(ans==1&&!flag)
                {
                    ans=0;
                    m++;
                    flag=1;
                }
                if(m==gen+1)
                {
                    cout<<"Possible"<<endl;
                    return 0;
                }
            }
            cout<<"Impossible"<<endl;
        }
    }
 
    return 0;
}

View Code